Thread by @cesifoti

While people's general understanding of physics is a jump from Newton to Einstein, it is important to understand that there are some very clear intermediate steps. Here, I want to focus on a huge one: Lagrangian and Hamiltonian mechanics (1/N)

Newton's greatest hit was his three laws of motion.
1. Inertia.
2. F=ma.
3. Action and reaction.
The key here is the second law, which allows you to write equations for the motion of things. For a spring ma=kx. For a falling rock ma=mgh.

Newton's equation allows you to connect the acceleration of an object (a=ẍ) with its position (x). If you solve that equation, you get the position in time (x(t)). That's great, but what equation do you need to solve? How do you figure what goes after ma=...?

As the eighteenth century moved forward, people began to work on systems that were much more complicated than a spring (mẍ=kx). People began to think about pulleys & hanging masses, & needed a way to deduce the Newton equation they needed to solve.

Lagrange and Hamilton figured out systems whose solutions are Newton's equations. That required of course, new abstractions and sophistications. It required figuring out a sort of purpose or principle for Newton's equations. Something they tried to "do" or preserve.

In physics, people talk about the principle of least action, & also, the conservation of symmetries. Lagrange & Hamilton discovered ways to express these principles in equations that existed for generalized coordinates.

Their equations did not care if you were using cartesian coordinates in a cube or spherical angles & a radius. They related to the idea of energy, and solving them gave you the equation you needed to solve to get the trajectory.

So if you had a complicated system of masses & pulleys, you did not need to scratch your head thinking about the sign of each variable. You could write a long expression for its potential & kinetic energy & use the Hamiltonian or Lagrangian method to find the equations of motion.

This repacked theoretical physics into a whole new level of abstraction & happened in the late 18th and 19th century. Lagrange (1736-1813) introduced his mechanics in 1788 Hamilton (1805-1865) introduced his in 1833

Lagrangian and Hamiltonian mechanics, however, are an essential intermediate step for what came later. And here, I don't just mean Einstein, but modern physics. In pop-culture Einstein & modern physics are synonyms (so I am simplifying here to communicate).

Modern Physics (particularly quantum mechanics and particle physics) is based on the idea of Hamiltonian or Lagrangian. In this case, you do get equations of motion (since the idea of trajectory doesn't make sense in the quantum world), but equations for "wave functions.."

which are related to clouds of probability rather than trajectories. Without this intermediate step (and many others), it is very hard to imagine the jump between Newtonian and Modern Physics. This intermediate step is in some way inevitable (as all big truths are) & essential.

Einstein's equation for gravity, while not being an example of Lagrangian or Hamiltonian mechanics, still builds on the idea of packing an equation in yet another layer of abstraction, although in Einstein's case, the equation is for a geometry rather than a trajectory

The purpose of this thread was to share this important, yet not so well known step. As a tidbit, consider the online popularity of Newton, Einstein, Lagrange and Hamilton, as measured by Wikipedia pageviews...

Newton's Wikipedia page receives between 250k to 400k pageviews a month pantheon.world/profile/person…
Einstein, from 400k to more than a million
pantheon.world/profile/person…
Lagrange receives from 8k to 16k
pantheon.world/profile/person…
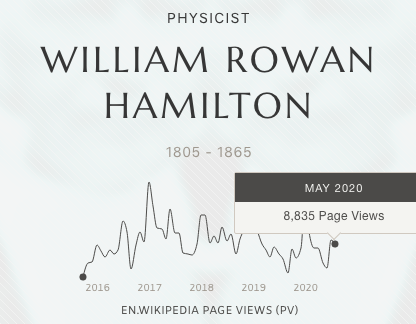
& Hamilton from 7k to 14k
pantheon.world/profile/person…

That means it takes from 3 to 10 years for the Hamilton page to receive the pageviews that Einstein gets in one month. Yet, they are of course, all giants standing in the shoulders of giants.