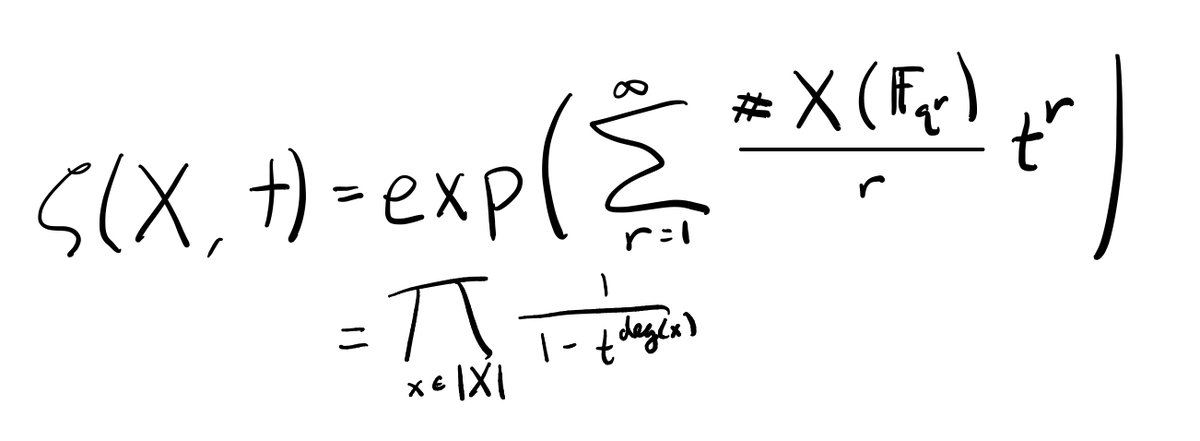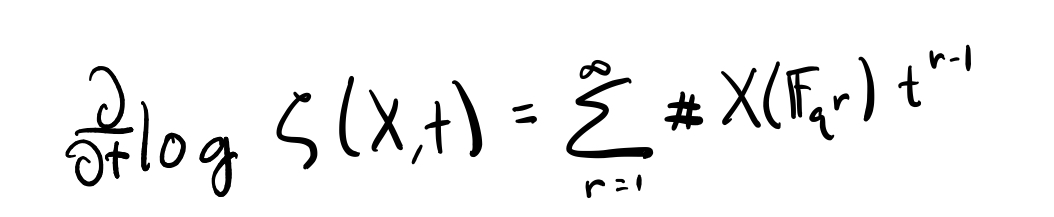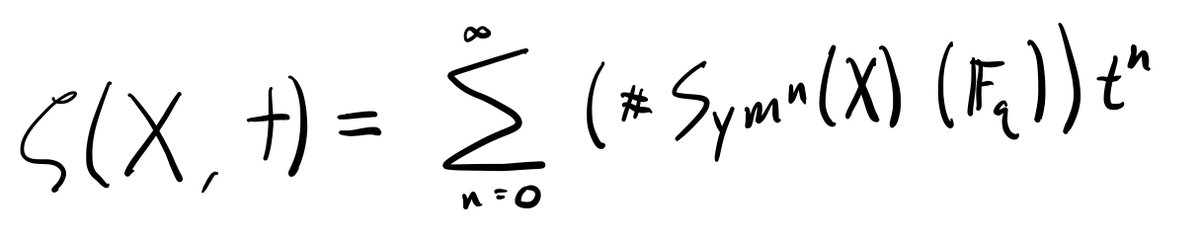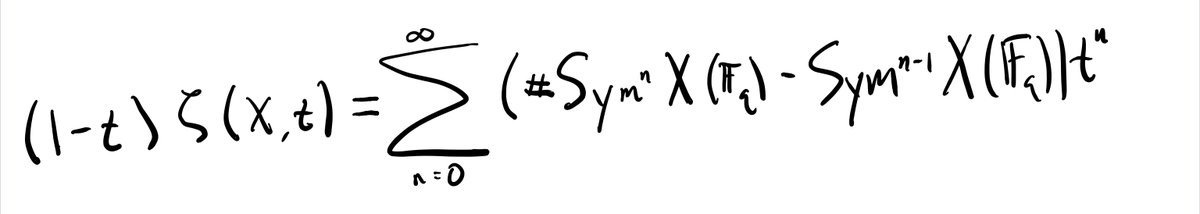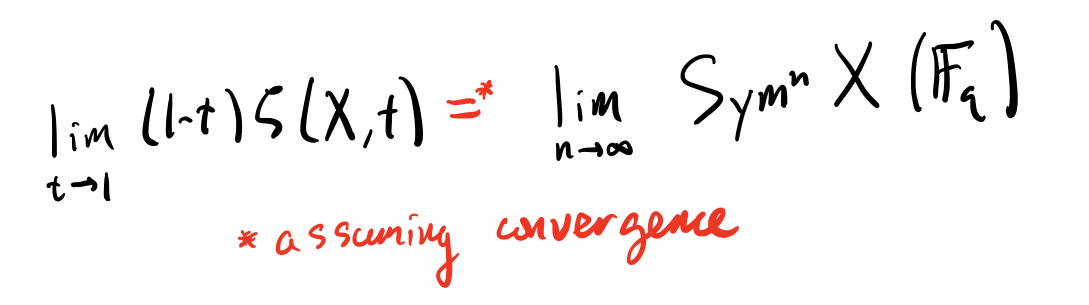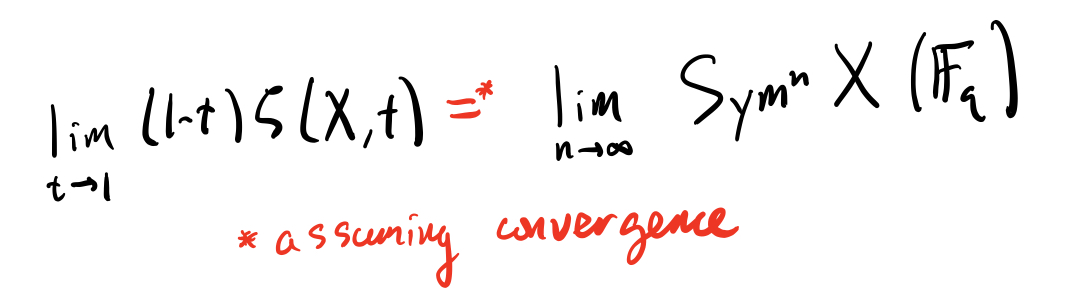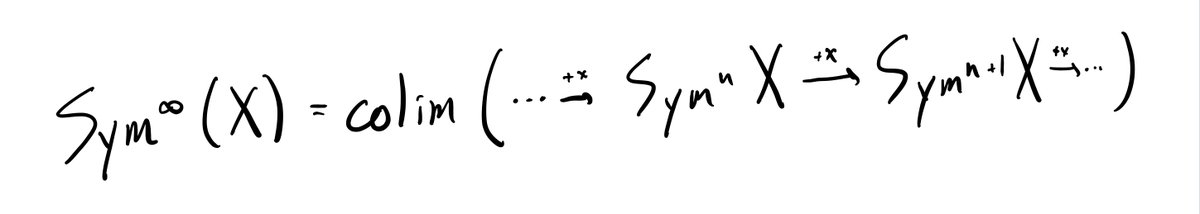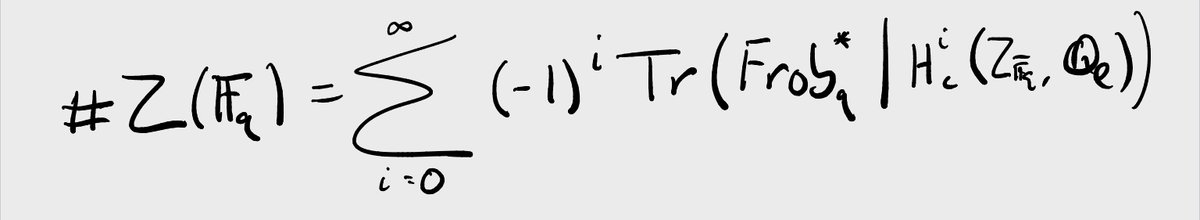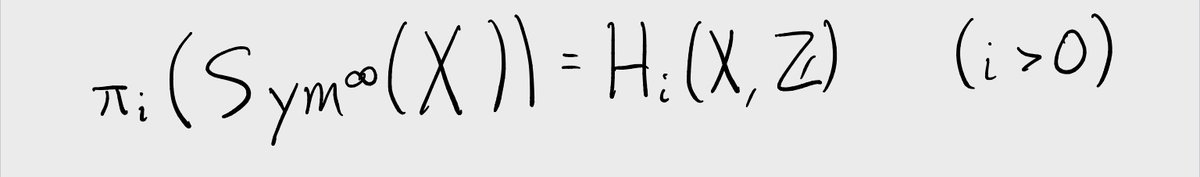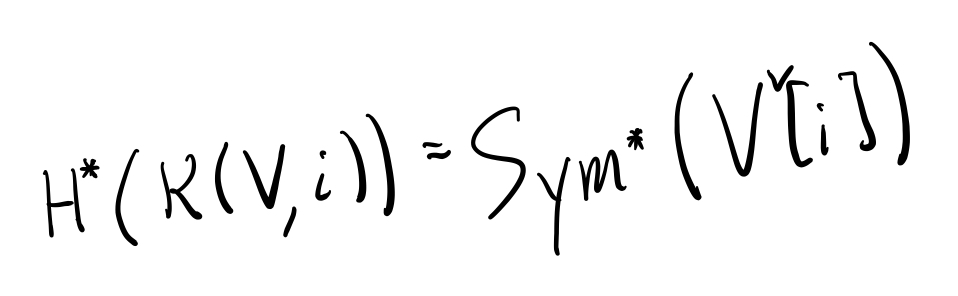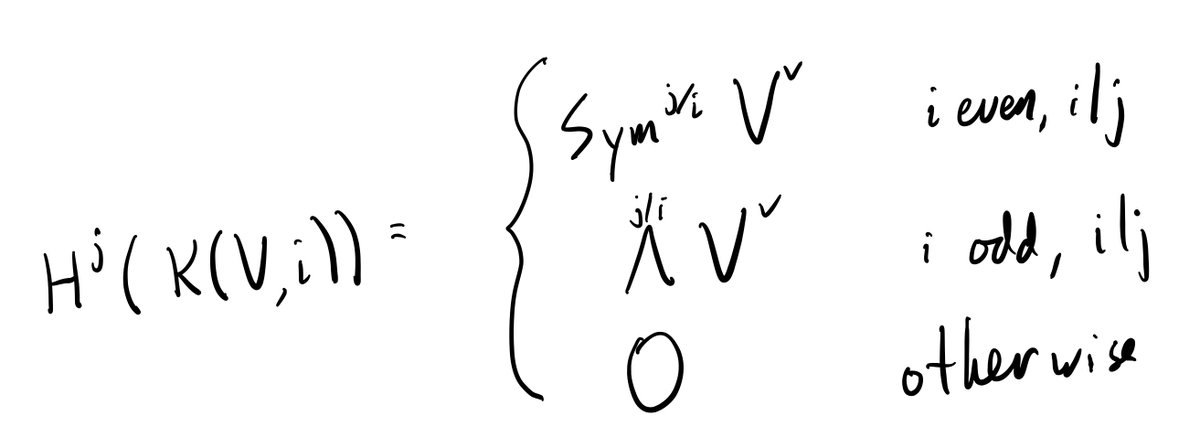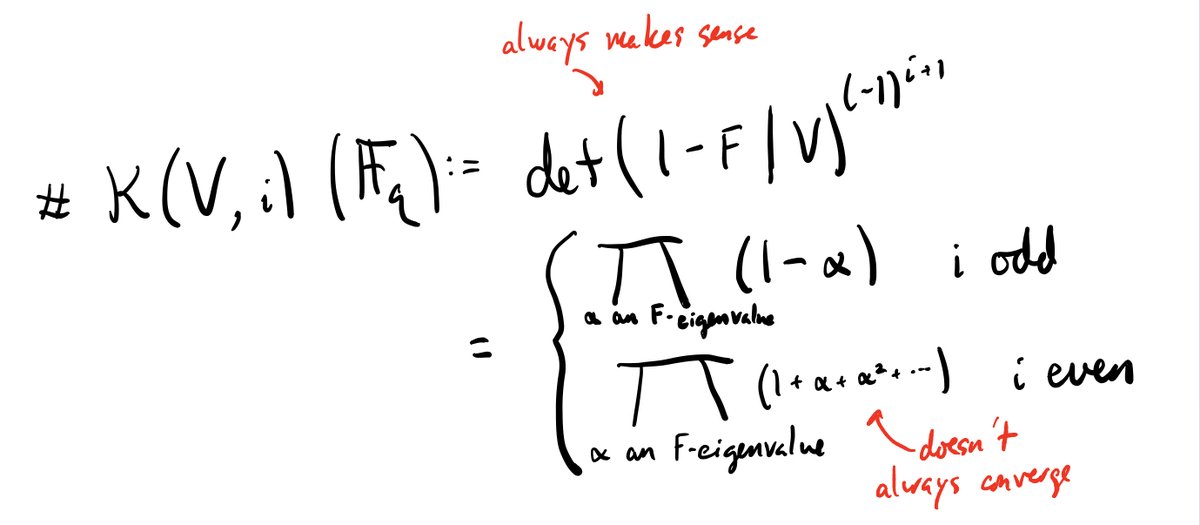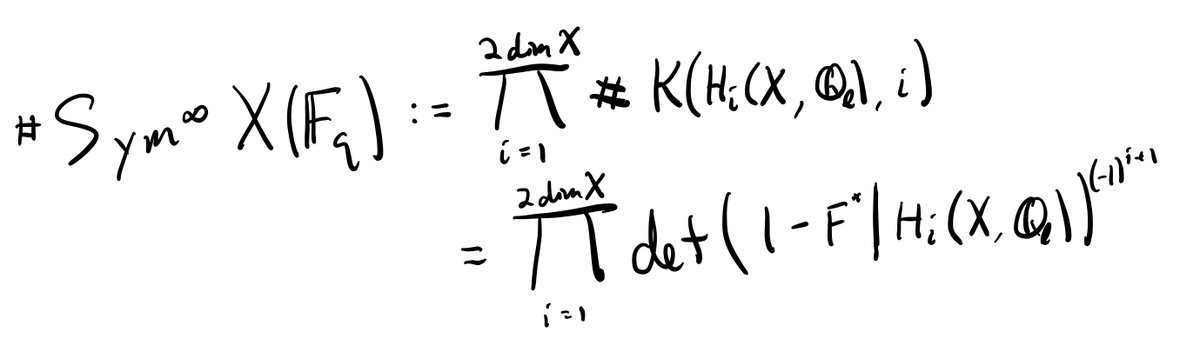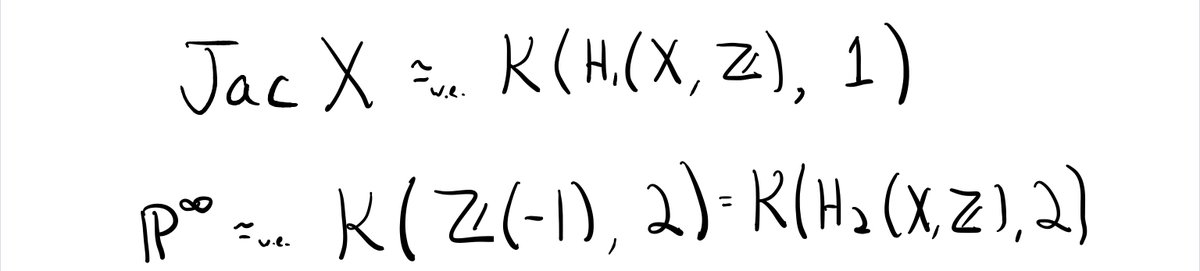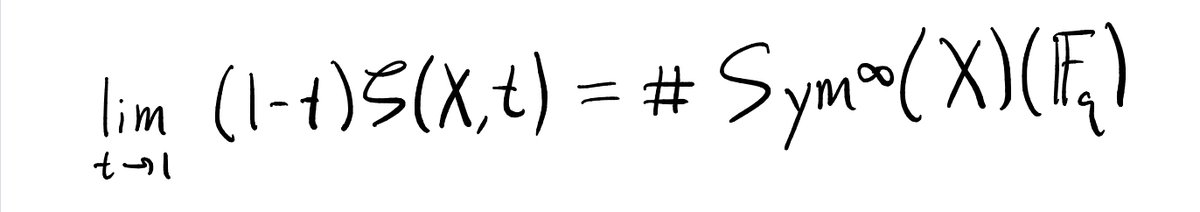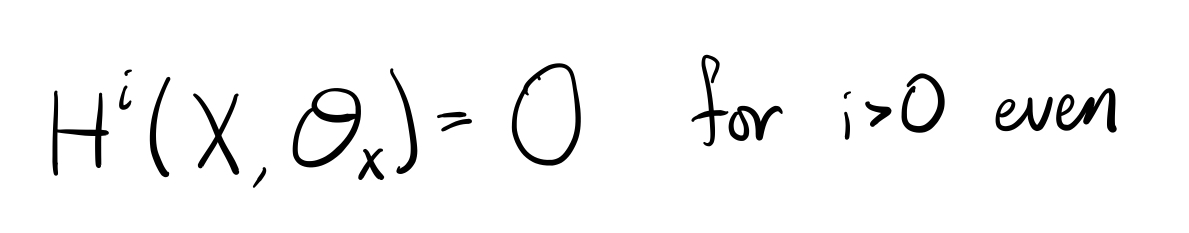Thread by @littmath

Thread, lost due to computer crash and recreated: a mysterious connection between number theory (the analytic class number formula) and algebraic topology (the Dold-Thom theorem). 1/n

The class number formula (below, from Wikipedia) tells us that the residue of the Dedekind zeta function of a number field K at s=1 is related to certain more algebraic invariants of the number field -- for example, its class number h_K and the number of roots of unity in K. 2/n

If you don't know what the Dedekind zeta function of a number field is, that's alright -- we'll replace it with a simpler object soon. It’s a generalization of the Riemann zeta function (the Dedekind zeta function of ℚ); the actual definition is below. 3/n

So here’s our "toy" model: the zeta function of a variety over a finite field. Let X/𝔽_q be a variety, defined by a bunch of polynomial equations with coefficients in 𝔽_q. The zeta function (below) records how many solutions these equations have over extensions of 𝔽_q. 4/n

Like the Riemann zeta function (and Dedekind zeta functions) this zeta function has an Euler product. In good cases it has a functional equation and some version of the Riemann hypothesis; it is the subject of the Weil conjectures, proven by Dwork, Grothendieck, and Deligne. 5/n

If the definition looks weird, note that its logarithmic derivative (below) is a generating series counting points of X over finite extensions of 𝔽_q. Slogan: the zeros and poles of a meromorphic function control the growth of the coefficients of its logarithmic derivative. 6/n

Before we dig into the analytic class number formula for this zeta function, we need a different description of it. Let Sym^n(X) be the quotient of X^n by the permutation action of the symmetric group on n letters. A point of Sym^n(X) is called an effective 0-cycle. 7/n

𝔽_q-points of Sym^n(X) ("rational effective 0-cycles") have a simple description; they're collections of Galois orbits of 𝔽_q-bar points of X with total size n. The Euler product description of zeta shows that it's a generating function for rational effective 0-cycles on X! 8/n

(9/n) Now let’s compute the residue of this zeta function at t=1. To do this, we multiply by (1-t) and take the limit as t-->1.

Multiplying by (1-t) gives:

(10/n) Now if t=1 is in the radius of convergence of this power series, we can just compute the limit by evaluating at t=1. The sum we get telescopes, giving the following equality (again, assuming the limit on the right makes sense):

OK, but this limit *never* exists, right? It’s the limit of an increasing sequence of integers, so we’re SOL.

Except that sometimes the limit exists p-adically! 11/n

Let's try an example. Suppose C/𝔽_q is a smooth proper curve of genus g. Then for n>>0, the Riemann-Roch theorem tells us that Sym^n(C) is a ℙ^{n-g}-bundle over Jac(X), the Jacobian of X. 12/n

So for n>>0, we can count the 𝔽_q-points of Sym^n(C): there are

|Jac(C)(𝔽_q)|(1+q+q^2+...+q^{n-g})

of them, because there are evidently |Jac(C)(𝔽_q)| points of Jac(C), and ℙ^{n-g} has (1+q+q^2+...+q^{n-g}) 𝔽_q-points. 13/n

Now if p is the characteristic of 𝔽_q, this converges p-adically as one takes n to ∞, because q is divisible by p; in fact, it converges to

|Jac(C)(𝔽_q)|/(1-q). 14/n

I claim that this is the class number formula for curves over finite fields.

Note that |Jac(C)(𝔽_q)| is the class group of C, and (1-q) is (up to a sign) the number of roots of unity in the ring of functions on our curve, just like with number fields. 15/n

For the rest of this thread, I want to try to make sense of the equation below, even when the limit does not converge, using ideas from algebraic topology: the Dold-Thom theorem. That is, I want to explain how the "class number formula" counts points on a certain space. 16/n

Choose x in X(𝔽_q). This gives us maps

Sym^n(X)-->Sym^{n+1}(X),

just by adding x to an n-tuple of points, to get an (n+1)-tuple. The infinite symmetric power Sym^∞(X) will be the union of all of the Sym^n(X).

17/n

Let's try to "count points" on this infinite-dimensional space Sym^∞(X). We can't do this naively; in any reasonable sense, this space has infinitely many points. Instead, we'll use the Grothendieck-Lefschetz trace formula, which tells us to count points using cohomology. 18/n

Taking Z above to be Sym^∞(X), we'll almost always get an infinite sum, but we'll find a way to regularize it.

So the question becomes: what's the cohomology of Sym^∞(X)? The answer -- given by the Dold-Thom theorem -- is well known to topologists. 19/n

The Dold-Thom theorem tells us that for a connected CW complex X, the i-th homotopy group of Sym^∞(X) is the same as the i-th singular homology group of X (as long as i is positive). We can use this to compute the (rational) cohomology of X. 20/n

For the purpose of computing rational homology (which is all the Grothendieck-Lefschetz trace formula cares about) we can pretend the infinite symmetric power is a product of Eilenberg-Maclane spaces. 21/n

So let's try to "count points" on K(V,i), where V is a vector space with Frobenius action. To do this, we'll compute the cohomology of K(V,i) and apply the Grothendieck-Lefschetz trace formula. Then we'll try to make sense of what comes out. 22/n

We know what the cohomology of K(V,i) is, though -- it's the following symmetric algebra (taken in the graded-commutative sense). I'll be more explicit in the next tweet. 23/n

(24/n) Explicitly, the cohomology of K(V,i) is given by the following formula (which depends on the parity of i):

Formally applying the Grothendieck-Lefschetz trace formula (if V is a vector space with Frobenius action) gives the second line below, which doesn't always make sense if i is even. But using the formula for a geometric series, we get the first line, which always makes sense! 25/n

Now that we've come up with a reasonable definition for the number of points on K(V,i), we can (using Dold-Thom as motivation) make an analogous definition for Sym^∞(X). 26/n

(27/n) Namely, since Sym^∞(X) is (for our purposes) a product of Eilenberg-Maclane spaces, we'll just *define* its point count to be the product of the corresonding point counts. That is:

(28/n) Let's see this at work for curves. Remember that the infinite symmetric power of a curve was a (infinite) projective space bundle over the Jacobian over the curve. But over ℂ, ℙ^∞ and the Jacobian are both Eilenberg-Maclane spaces:

Moreover our new definition of a "point count" for Sym^∞(X) gives precisely

|Jac(X)(𝔽_q)|/(1-q).

That is, it's our "class number formula" from before. (29/n)

Now here's the punchline. For any smooth projective variety over 𝔽_q whatsoever, the residue at t=1 of the zeta function is *always* the "number of points" of Sym^∞(X), under our definition via Dold-Thom. We've found a geometric interpretation of the class number formula. 30/n

Note that this is true even when the limit from before doesn't converge p-adically (for example, the limit doesn't converge for most K3 surfaces). It's an algebro-geometric avatar of Dold-Thom. 31/n

(32/n) One final remark -- you might reasonably ask when the limit we've managed to "regularize" does in fact converge p-adically. It's actually not so hard to give a good answer (and worth doing yourself). One special case -- it happens when X has certain cohomology vanishing:

Anyway, if you've made it this far, hopefully you've found this connection between the class number formula and Dold-Thom as interesting as I do! (33/n, n=33)