#数楽
添付画像
1. 高木貞治『解析概論』のpp.123-124より
(大学で数学を専攻していれば知っているはずの話)
2. y²=x²+1の場合の計算例
二次曲線をパラメトライズする有理函数は二次曲線の1点を通る直線とのもう1つの交点を考えば作れます。二次曲線一般の様子を理解する問題に帰着。

添付画像
1. 高木貞治『解析概論』のpp.123-124より
(大学で数学を専攻していれば知っているはずの話)
2. y²=x²+1の場合の計算例
二次曲線をパラメトライズする有理函数は二次曲線の1点を通る直線とのもう1つの交点を考えば作れます。二次曲線一般の様子を理解する問題に帰着。
https://twitter.com/f_sei/status/1305120656086855680


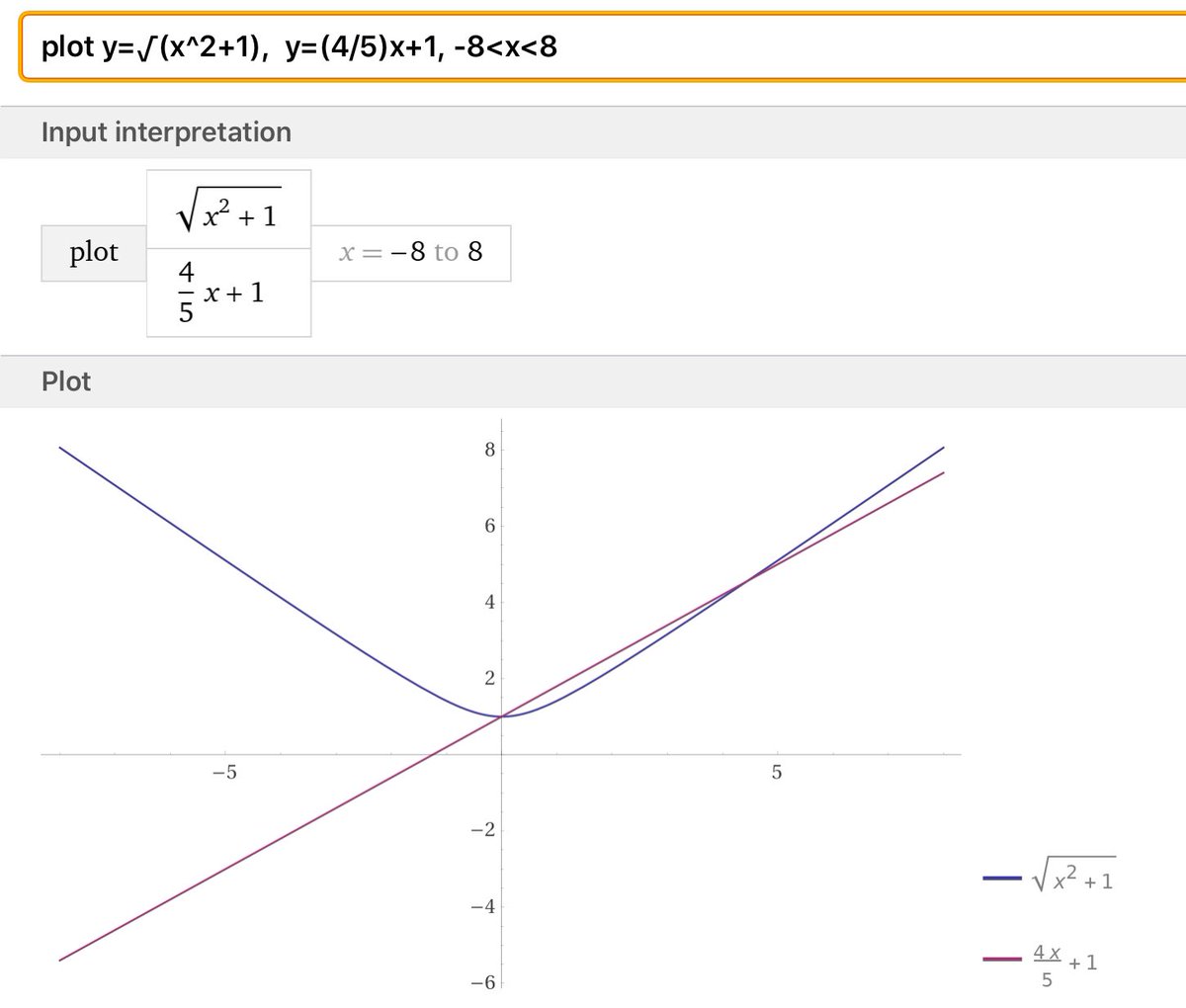
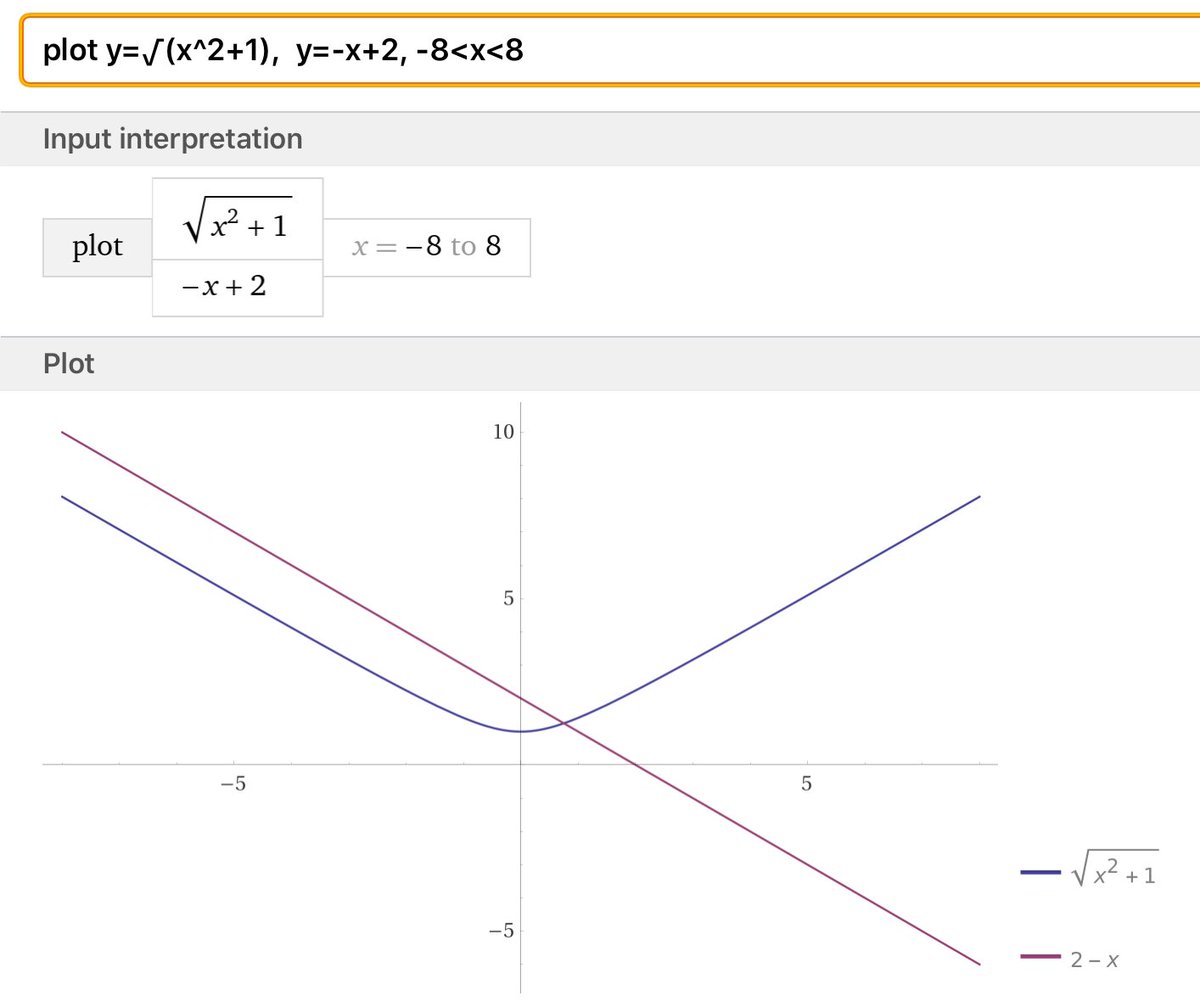
#数楽 双曲線と直線の交わり方の図
多くの場合に数学では式だけを書いちゃダメで図も描いて幾何的な直観も使った方がお得。
この手の情報は「受験数学」というくだらない発想を捨てさえすれば比較的容易に手に入るはず。
wolframalpha.com/input/?i=plot%…
wolframalpha.com/input/?i=plot%…

多くの場合に数学では式だけを書いちゃダメで図も描いて幾何的な直観も使った方がお得。
この手の情報は「受験数学」というくだらない発想を捨てさえすれば比較的容易に手に入るはず。
wolframalpha.com/input/?i=plot%…
wolframalpha.com/input/?i=plot%…
#数楽
定理:nが3以上の整数のとき、曲線 xⁿ+yⁿ=1 をパラメトライズする有理函数の組 (x, y) = (f(t), g(t)) が存在しない。
この結果はフェルマー予想(もしくは最終定理)の有理函数版で、証明は数論的なオリジナルのフェルマー予想よりずっと易しいです。
定理:nが3以上の整数のとき、曲線 xⁿ+yⁿ=1 をパラメトライズする有理函数の組 (x, y) = (f(t), g(t)) が存在しない。
この結果はフェルマー予想(もしくは最終定理)の有理函数版で、証明は数論的なオリジナルのフェルマー予想よりずっと易しいです。
#数楽 これは、高校数学+α程度で理解できる
実射影平面上の二次曲線の代数幾何
に関する話だと思えます。実平面に無限遠(地平線)を付け加えて、180度反対側の無限遠点を同一視してできるのが実射影平面です。絵を描くときには地平線も描くので、これが現実で役に立つ幾何になっています。
実射影平面上の二次曲線の代数幾何
に関する話だと思えます。実平面に無限遠(地平線)を付け加えて、180度反対側の無限遠点を同一視してできるのが実射影平面です。絵を描くときには地平線も描くので、これが現実で役に立つ幾何になっています。
#数楽 以前、オープンキャンパスでもネタにしたのですが、
無限に広い平面上に描かれた放物線(や双曲線や楕円)を
写生するとどのような絵が描かれるか?
という問題を何でもありで解くと理解が進むと思います。
実射影平面上では、楕円、放物線、双曲線が「統一」されます!
無限に広い平面上に描かれた放物線(や双曲線や楕円)を
写生するとどのような絵が描かれるか?
という問題を何でもありで解くと理解が進むと思います。
実射影平面上では、楕円、放物線、双曲線が「統一」されます!
#数楽 実射影平面の無限遠点全体は実射影直線をなすのですが、3つの別のものに見えていた二次曲線達は単に無限遠射影直線との交わり方の違いしかないことが分かります。
無限遠射影直線と
交わらない⇔楕円
接する⇔放物線
2点で交わる⇔双曲線
無限遠射影直線と
交わらない⇔楕円
接する⇔放物線
2点で交わる⇔双曲線
#数楽 例えば、双曲線y²=x²+1は無限遠射影直線と
(∞, ∞) = (-∞,-∞)
(∞,-∞) = (-∞, ∞)
の2点で交わります。後者のを通る直線と交わるy²=x²+1上の別の点を考えることが
t = x + y (= √x + √(x²+1))
という変数変換の正体になっています。
高木貞治『解析概論』の読者にとっては常識?
(∞, ∞) = (-∞,-∞)
(∞,-∞) = (-∞, ∞)
の2点で交わります。後者のを通る直線と交わるy²=x²+1上の別の点を考えることが
t = x + y (= √x + √(x²+1))
という変数変換の正体になっています。
高木貞治『解析概論』の読者にとっては常識?
#数楽 このスレッドを最初から読めば、高木貞治『解析概論』の不定積分の求め方の節を読むだけでも、大学受験で少し有利になったり、受験生への数学の指導において本質を突いた説明が可能になることが分かると思います。
#数楽 実射影平面上の二次曲線について
放物線⇔無限遠射影直線と接する
であることは、絵心のある人であれば、数式の助けを借りずに、絵を描くだけで認識できると思います。
画板上に放物線は地平線に接する楕円として描かれるはずです。
私も手で頑張って描いて納得できました!
放物線⇔無限遠射影直線と接する
であることは、絵心のある人であれば、数式の助けを借りずに、絵を描くだけで認識できると思います。
画板上に放物線は地平線に接する楕円として描かれるはずです。
私も手で頑張って描いて納得できました!
https://twitter.com/genkuroki/status/1305531484548157440
#数楽 検索すれば出て来ると思いますが、この話題はツイッターですでに何度もしていて、
放物線に囲まれた大陸が地平線に接する様子のCGが欲しい
という話もしたはず。美しい大陸ならさらによい。
今ならJuliaを使って自分で描けるんじゃないか?
個人的には「芸術家」の作品を見たい。
放物線に囲まれた大陸が地平線に接する様子のCGが欲しい
という話もしたはず。美しい大陸ならさらによい。
今ならJuliaを使って自分で描けるんじゃないか?
個人的には「芸術家」の作品を見たい。
#数楽 近似的な球体上に住んでいる我々が見ることができない様子を見たい。
#数楽 おお!このスレッドのずっと上の方で説明したことが、高校生向けの参考書にも書いてあるらしい。
射影平面は一度理解してしまうと「普通はそのように考える」という類のものの1つになってしまう。
このスレッドで説明したように「写生」ともろに関係がある。
射影平面は一度理解してしまうと「普通はそのように考える」という類のものの1つになってしまう。
このスレッドで説明したように「写生」ともろに関係がある。
https://twitter.com/masa_cosmos/status/1306384626789748736
• • •
Missing some Tweet in this thread? You can try to
force a refresh