
私については https://t.co/WbWjr95AmF と https://t.co/P7WOMn2ay1 と https://t.co/ouhJUcBE7E と https://t.co/Zzel9GBOCm を見て下さい。
4 subscribers
How to get URL link on X (Twitter) App

https://twitter.com/lester_domes/status/1312827596522975232#統計 特定の統計モデルの下で、現実世界で得たデータの数値とモデルのパラメータの値の相性の良さ(compatibility)の指標であるP値が与えられているとき、P値が5%以上になるパラメータの値全体が95%信頼区間になる。
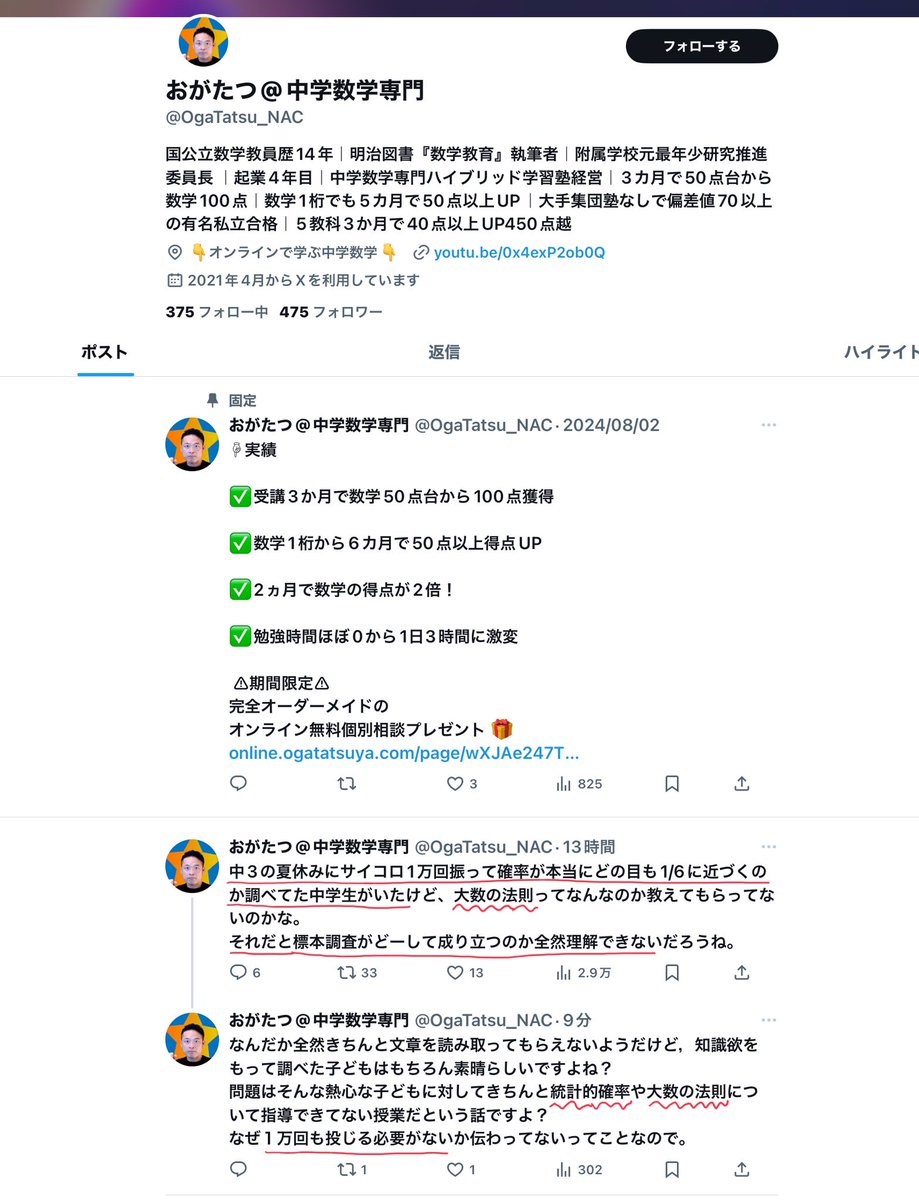
https://twitter.com/genkuroki/status/1829301268613042318
 #統計 以下のリンク先の反応も理解していない側に分類されると私は思いました。
#統計 以下のリンク先の反応も理解していない側に分類されると私は思いました。

https://twitter.com/shuntarooo3/status/1798191137481695258
 #統計 「違いがない」の型の帰無仮説のP値をnull P値と呼びます。
#統計 「違いがない」の型の帰無仮説のP値をnull P値と呼びます。
https://twitter.com/ien_enjoy/status/1669298004761923584#統計
https://twitter.com/hiyori13/status/1669766248702545923上野千鶴子は、自閉症の原因について母子密着説を唱えていたのですが、それが誤りであることが定説になっていることを指摘された後には、定説と上野千鶴子的なトンデモ説を平等に扱うという態度を取りました。
https://twitter.com/genkuroki/status/1117307443560583170
https://twitter.com/genkuroki/status/1669399159793938432環k上の環Aで表現された方程式のk上の環Bでの解集合はk上の環準同型全体の集合
https://twitter.com/temmusu_n/status/1667751068191850497教科書に従って「a(3x-6y)は誤りで、3a(x-2y)が正解だ」と安易に教えてしまった中学校の数学の先生は
https://twitter.com/esumii/status/1285792551904010240

https://twitter.com/Shuntarooo3/status/1628297493007192064

 #統計 実際、natureの記事 nature.com/articles/d4158… ではcompati{ble,bility}が重要キーワードになっており、P値が
#統計 実際、natureの記事 nature.com/articles/d4158… ではcompati{ble,bility}が重要キーワードになっており、P値が

https://twitter.com/hiyori13/status/1516327988572303360#統計

https://twitter.com/shuntarooo3/status/1451809386830000130#統計 例で説明します。


https://twitter.com/genkuroki/status/1619213870924713984#統計 帰無仮説は統計モデルのパラメータの値に関する仮説になっており、P値を得るための確率の(近似)計算は帰無仮説下の統計モデル内で行うことになるので、統計モデルについての説明がない仮説検定の説明は最初から相手にする価値がないということになります。
https://twitter.com/tkawai18_tkawai/status/1619106617915756546#数楽 Ta(n+1)=a(n)と書く。
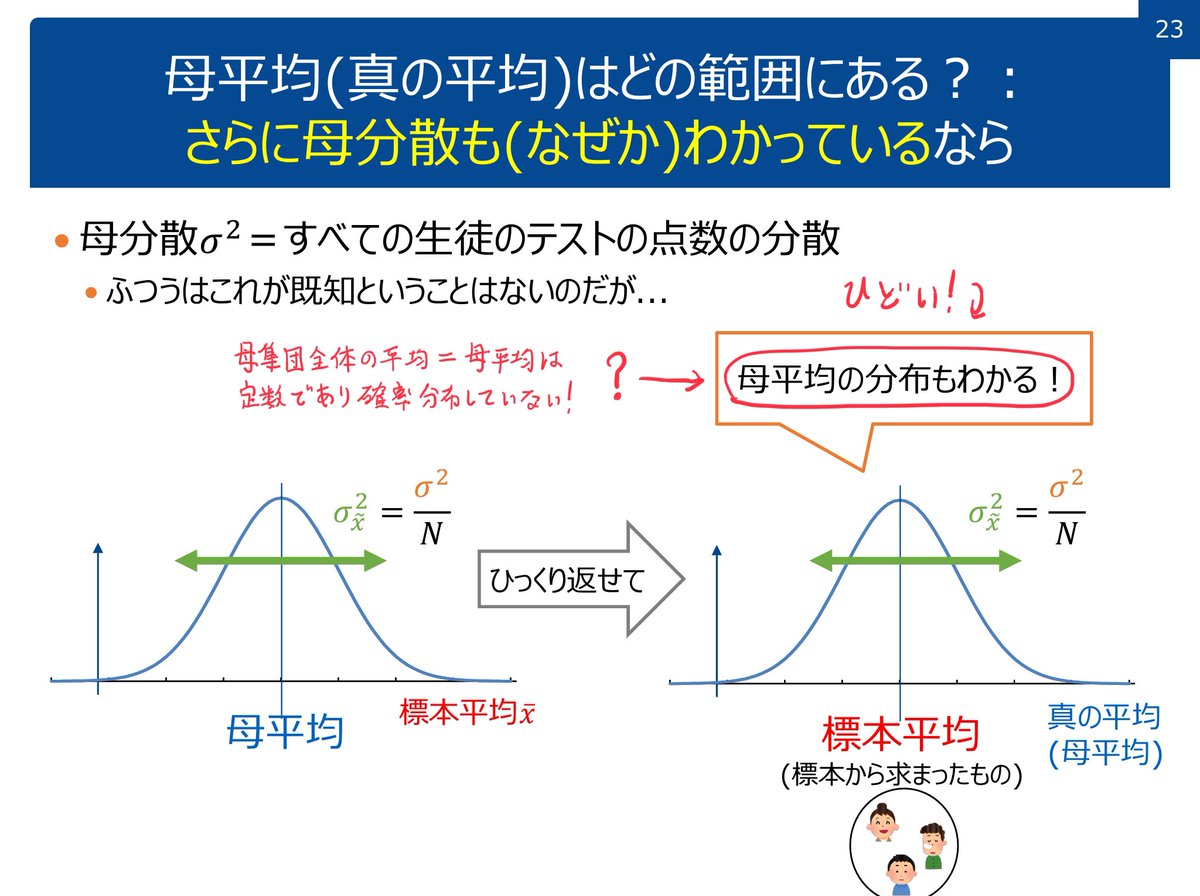
https://twitter.com/biomedicalhacks/status/1619087098878779398

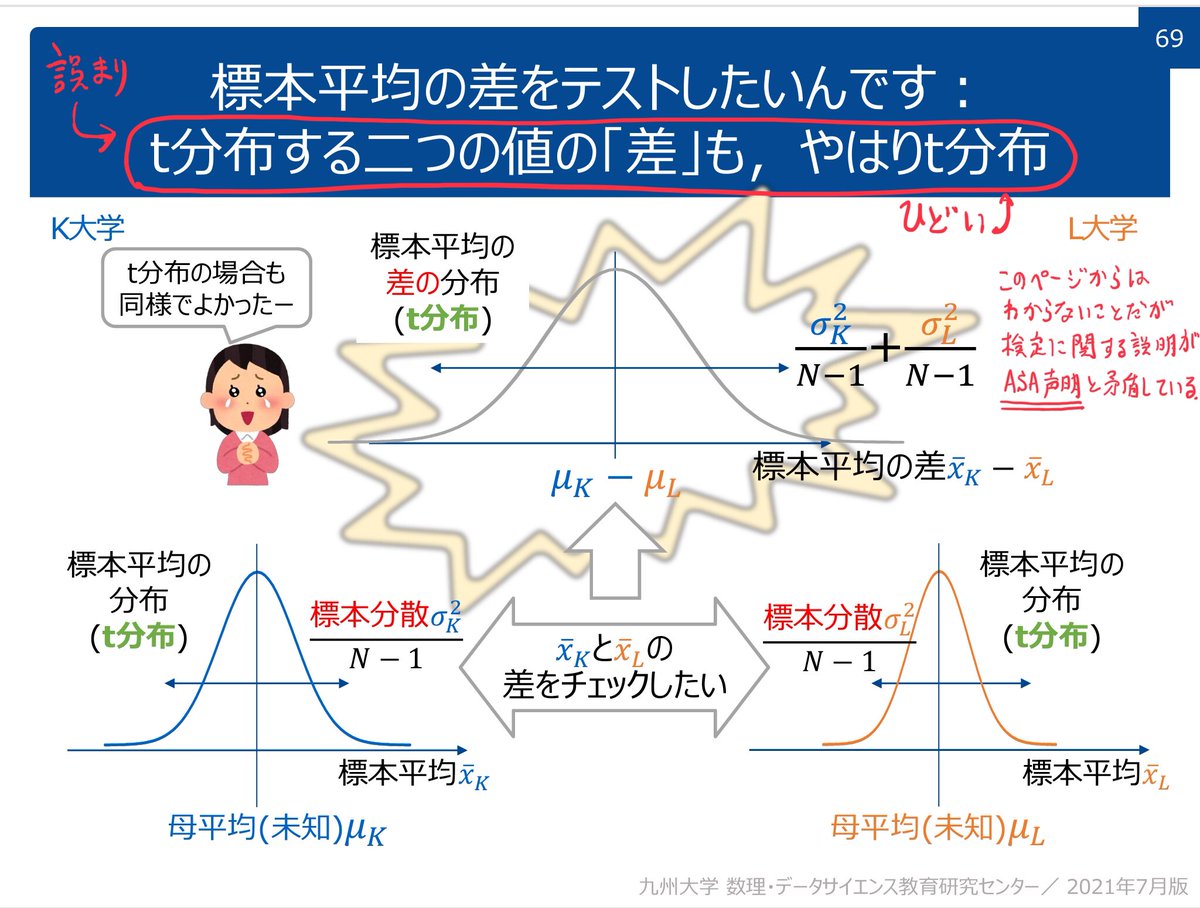
 #統計 P値や信頼区間に関するより現代的な知識は論文 journals.sagepub.com/doi/10.1177/02… で得られる。
#統計 P値や信頼区間に関するより現代的な知識は論文 journals.sagepub.com/doi/10.1177/02… で得られる。https://twitter.com/genkuroki/status/1614516806009647104



https://twitter.com/genkuroki/status/1618322465134112768
 #統計 ある程度以上、統計的因果推論について学んだ人であれば、Cによる条件付けで調整すると、EのOutcomeへの効果にバイアスが生じ、因果効果の見積もりを誤る危険性があることを理解しているはずです。
#統計 ある程度以上、統計的因果推論について学んだ人であれば、Cによる条件付けで調整すると、EのOutcomeへの効果にバイアスが生じ、因果効果の見積もりを誤る危険性があることを理解しているはずです。
https://twitter.com/genkuroki/status/1618669516128661505#統計 c=a+hとおくと、

https://twitter.com/genkuroki/status/1618002371585671174#統計 例えば、変数XとYの関係を調べたいとき、Xが他の変数Zに影響されて決まる状況(例えば観察研究)と、ZのXへの影響を断ち切ってXのZと無関係に決まるようにした状況(例えばランダム化{比較,対照}試験)では、別の統計モデルを使う必要があります。