Thread by @polfosol

یه جا دیدم نوشته بود افغان‌ها به زنی که حامله‌ست میگن دوجان. یعنی کسی که دوتا جان در بدن داره 😍
انقدر قشنگ بود حسابی رقیق شدم ♥️♥️
حیفم اومد با شما به اشتراک نذارمش.

این اسم علاوه بر زیبایی فوق‌العاده‌ش خیلی هم کاربردیه. میشه داده‌های متعددی رو با این روش و تنها با گفتن یک کلمه انتقال داد؛ ازجمله جنسیت نوزاد، تعداد و حتی سنشون.

به عنوان مثال، فرض کنید تعداد کروموزوم‌های X مبنای شمارش باشه و هر کروموزوم رو 0.5 واحد حساب کنیم.

اون‌وقت دوجان یعنی زنی که حامله‌ست و نوزادش دختره.
وقتی که نوزاد پسر باشه میشه 1.5جان، چون پسرها یک کروموزوم X دارن. پس با این روش فشرده‌سازی (data compression) درعین افزایش داده‌های انتقالی، حجم اطلاعات هم کمتر میشه.

اما برای هرنوع فشرده‌سازی داده، باید یک پروتکل تعریف بشه /

که فرستنده و گیرنده بهش تسلط داشته باشن.
مشکل دیگه‌ای که این روش داره احتمال تداخل داده‌هاست. مثلا وقتی گیرنده عبارت دوجان رو دریافت می‌کنه حق داره بپرسه آیا منظور حاملگی با یک جنین دختره یا دوقلوهای پسر؟

این «ایزومر»ها تقریبا درهر روش فشرده‌سازی ممکنه به‌وجود بیان.

پس طراح پروتکل باید برای جداسازی ایزومرها هم تدابیری پیش‌بینی کنه.
فرمول شیمیایی مواد یک روش فشرده‌سازی برای بیان ساختار مولکولی اونهاست. برای موادی که ایزومر دارن این فرمول به‌گونه‌ای تغییرمی‌کنه که از میزان فشردگی داده‌ها کاسته میشه. ولی درعوض ساختار مولکولی به‌درستی منتقل میشه

مثلا فرمول فشرده اسید استیک C2H4O2 هست.
اما این ایزومرهایی که تو این شکل‌ها می‌بینید فرمول مشابهی دارن. لذا اسید استیک رو به‌صورت CH3COOH می‌نویسن تا معلوم بشه در مولکول مربوطه هم هیدروکسیل داریم و هم کربونیل. یا مثلا گلیکولالدهید با فرمول HOCH2CHO مشخص میشه و قس علی هذا.

برای تمایز ایزومرهای دوجان هم میشه به حاملگی با جنین دختر گفت دوجان و برای دوقلوهای پسر از 0.5-1.5جان استفاده کرد.
***

یه نکته کاربردی دیگه بگم. در سیستم‌های مخابراتی برای صرفه‌جویی در کانال انتقال، داده‌های مجزا رو روی فرکانس‌های مختلف سوار می‌کنن. به این فرکانس‌ها میگن carrier

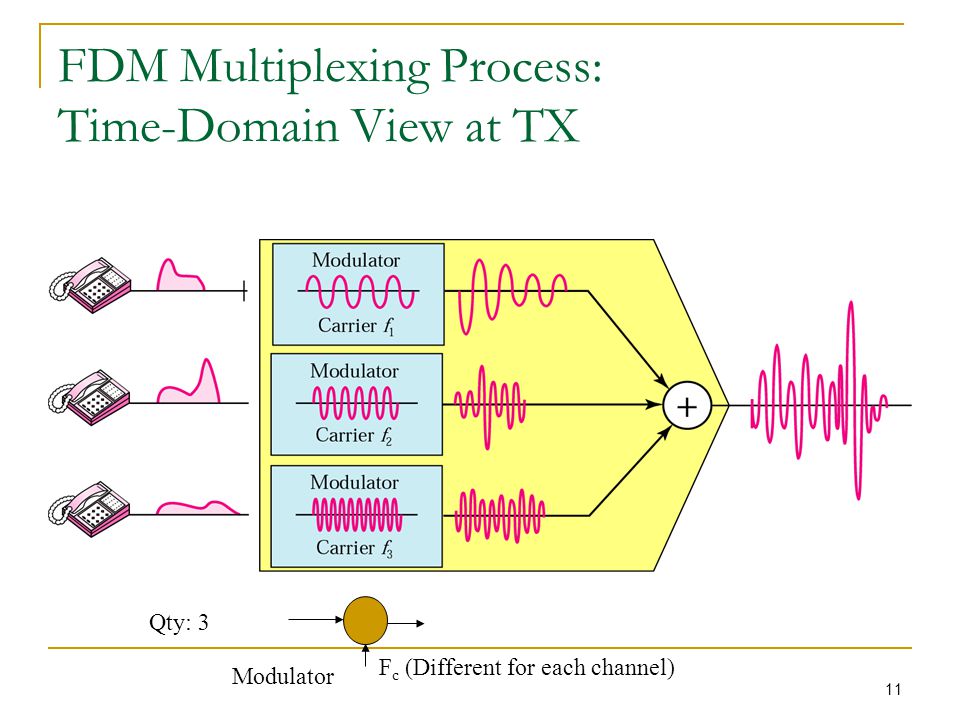
اون‌وقت سیگنال‌هایی که روی کریِر سوار شدن با هم جمع میشن و سیگنال حاصل تنها ازطریق یک کانال منتقل میشه. اگر فرکانس‌های کریر به اندازه کافی از هم فاصله داشته باشن میشه با خیال راحت گفت که نه داده‌ای گم میشه و نه تداخلی ایجادمیشه.

حالا می‌تونیم این‌طور درنظر بگیریم که تو مثال ما /

سیگنال‌های مربوط به تعداد دخترها و پسرها هرکدوم روی یک ضریب (carrier) سوار شدن که برای پسر 0.5 و دختر 1 ــه. باتوجه به اینکه کریر دختر و پسر به هم نزدیکه احتمال تداخل و ازدست‌رفتن اطلاعات بالاست.
اگر فرکانس کریر پسرها مثلا 0.1 بود با اطمینان بالایی می‌شد گفت تداخل به وجود نمیاد /

و فاصله‌ی کافی بین کریرها وجود داره؛ چون تعداد پسرها (پهنای باند) قاعدتاً از ۱۰ کمتره.
(درواقع رکورد تعداد چندقلوزایی در تاریخ ۸تا بوده ↓)

خب حالا که تا اینجا اومدین اینم اضافه کنم که گیرنده برای دیکد کردن پیام ارسالی ما باید یه جور معادله ریاضی حل کنه.
nytimes.com/2018/12/15/sty…

فرض کنید تعداد جنین دختر با f و پسر با m مشخص شده و تعداد جان‌ها برابر j هست. اون‌وقت با معلوم بودن j باید معادله زیر را برای مجهولات m و f حل کرد:
1+f+0.5m
=j
دقت کنید یک معادله داریم و دو مجهول. یعنی مجهولات از معادلات بیشتره. ضمنا مجهولات ما فقط می‌تونن اعداد صحیح نامنفی باشن.

به این معادلات میگن معادلات دیوفانتی (Diophantine) که از مهم‌ترین شاخه‌های نظریه اعداده.
درواقع مثال ما ساده‌ترین نوع معادله دیوفانتی هست که بهش میگن معادله دیوفانتی خطی، و اقلیدس روش ساده‌ای برای حلش پیدا کرده.
(حاشیه: قضیه فرما هم یک معادله دیوفانتی بود)

https://twitter.com/polfosol/status/1246471282583048197

به هرحال، ما یک معادله دیوفانتی خطی داریم به‌شکل af+bm=J که مجهولاتش نمی‌تونن منفی باشن. اگر ضرایب a و b نسبت به هم اول باشن، این معادله درحالت کلی بی‌نهایت جواب داره. اما در مجموعه اعداد نامنفی احتمالا جواب‌هاش محدود یا حتی یکتاست.

پس نکته‌ی آخر اینکه در پروتکل مدنظر ما، /

جلوگیری از تداخل داده‌ها یا تولید ایزومر معادل با این مساله‌ست که ضرایب این معادله‌ی خطی دیوفانتی رو طوری تعیین کنیم که معادله‌ی حاصل در فضای جواب (اعداد صحیح نامنفی با شرط f+m<10) حلّ یکتا داشته باشه.

این مساله‌ی جالبیه که بعدا اگه عمری باقی بود بیشتر درباره‌ش توضیح میدم.