Share this page!

Enter URL or ID to Unroll

You can paste full URL like: https://x.com/threadreaderapp/status/1644127596119195649
or just the ID like: 1644127596119195649

How to get URL link on X (Twitter) App

  1. On the Twitter thread, click on or icon on the bottom
  2. Click again on or Share Via icon
  3. Click on Copy Link to Tweet
  4. Paste it above and click "Unroll Thread"!
  5. More info at Twitter Help
黒木玄 Gen Kuroki Profile picture
@genkuroki
Oct 31, 2020 • 692 tweets • >60 min read • Read on X
#統計 新刊の大塚淳著『統計学を哲学する』を近所の本屋で買って来ました。まだp.91にしか目を通していないのですが、

【データに基づく信念の改定というベイズ流の考え方】

とか

【ベイズ統計～ベイズ主義では確率は主観的な信念の度合いを測るもの】

と書いてあった！これはひどいと思いました。 Image
#統計 現実の統計分析や機械学習でベイズ統計の技術が「データに基づく信念の改定」としては普通使われていません。

数学的モデルとしての確率分布は使われていますが、モデル内における確率をわざわざ「主観的な信念の度合い」などと解釈したりしません。続く
#統計 去年の12月に出版された浜田宏他著『社会科学のための ベイズ統計モデリング』という本を見れば、社会科学の分野においても理解度の高い人たちにとって、ベイズ統計はすでに「主観確率」の「ベイズ主義」によるものではなくなっていることが分かります。続く
#統計 さらに、大学でのベイズ統計のある講義では添付画像のように、「主観確率」による「ベイズ主義」によるベイズ統計は廃されており、ベイズ統計は「数学で推測が当たる道を作る」方法の1つに過ぎないという扱いになっています。

watanabe-www.math.dis.titech.ac.jp/users/swatanab…
「主義」 を心配するみなさまに
渡辺澄夫
#統計 そして、Stanなどでベイズ統計の実践をすでにやったことのある人達は、ベイズ統計を使っていても「データによって信念を改定した」などとは思っていないはずです。

「主観確率」の「ベイズ主義」に基づくベイズ統計の解釈は実践レベルではとっくの昔に終わっているのです。続く
#統計 ところが、大塚淳氏曰く

【この本は何を目指しているのか。その目論見を一言で表すとしたら、「データサイエンティストのための哲学入門、かつ哲学者のためのデータサイエンス入門」である。】

それならば、「主観確率」の「ベイズ主義」をきちんとゴミ箱に捨ててからそうするべきでした。
#統計 p.91を見た私の第一印象は最悪に近いというのは変えようがない事実。

しかし、以上のコメントはp.91にしか目を通していない段階でのコメントなので、後で撤回して、別のコメントをするかもしれません。

重要な訂正がある場合にはこのスレッド内で行います。
#統計 検索するとこの本をすでに購入した人たちが沢山いるようですが、まだ誰も「主観確率のベイズ主義に基づく統計学」=「ベイズ統計」という見方に対する否定的なコメントは出ていないと思う。(見逃していたらごめんなさい。)

いち早く本を買った人はそういうコメントを出すべきだったと思う。
#統計 「データサイエンス」とか言いながら、ベイズ統計を「主観確率」の「ベイズ主義」に基いて語っている時点でアウト。

頻度論との関係とは無関係にアウト。

この点について知らなかった読者は気を付けた方がよいと思う。

論外にダメな所はきちんと否定してまともな部分だけを選んで読めばよい。
#統計 数学が絡む話題ではどうしても理解度に大きな差が出てしまいます。

『社会科学のためのベイズ統計モデリング』の著者の浜田さんのように数学的理解力に秀でているおかげで、「主観確率」だとか「ベイズ主義」の類に頼らずにベイズ統計を理解してしまう人達に見習うことは多いと思います。
#統計 統計学のようなややこしい話題で致命的にどうしようもないことを書かずに済ませることは私は難しいと思う。

特にベイズ統計は数学的にややこしい話です。
#統計 おお！著者まで伝わった！

古典統計や頻度主義といった話題との関係とは無関係に、この21世紀に「主観確率」の「ベイズ主義」でベイズ統計について語るのはまずいです。
#統計 非常に細かいコメント

【】内は引用

p.13の5行目【統計量(statistics)】とstatisticがなぜか複数形になっていた。
#統計 数式の書き方へのコメント

p.13の下から6行目以降の数式では

n
Σ
i=1

の意味で

n
Σ
i

と"=1"が略されて書かれている。

一般に数学が苦手な読者にも読んでもらいたい場合には、この手の略記はかなりのリスク要因になります。
#統計 この本での「確率モデル」という用語の使い方は、読者を混乱させる可能性があると思ったので、1ツイートで収まらないコメントをします。

一般の読者には非常に申し訳ないのですが、数学用語を断り無しで使います。

最後の方で数学を知らなくてもよい話もする予定。続く
#統計 まずは細かい誤植の指摘

p.23の下から3行目に

【R2　ある部分集合A∈Ωが事象なら～】

と書いてあるが、この "∈" の使い方は誤りです。A⊂Ω と書くべきでした。

もしくは、σ-algebraにも例えば𝓕のような記号を割り振って、A∈𝓕と書けばよかった。続く
#統計 pp.23-25では、σ-algebraや確率測度の定義をして、通常の数学用語では「確率空間」と呼ばれるものについて純粋に数学的に説明しようとしているのですが、なぜかその節に付けられたタイトルが【2-1　確率モデル】になっています。続く
#統計 この本での「確率モデル」という用語の使い方はp.21の脚注1で説明されています(添付画像)。

データの背後に確率法則を想定することと、純粋に数学的に確率空間を考えることは概念的に異なる。

哲学の話をしたいなら、そういう概念的な違いについて繊細な態度を取って欲しかったです。続く Image
#統計 あと、数学的に真面目に確率空間及び関連の概念について説明すると、読者が数学の難しさに負けて、何か深いことを言っているかのように誤解する可能性があります。続く
#統計 ツイッターで繰り返し述べているように、測度論的な確率概念の定式化は、「確率とは何か」のような問題を避けて、0以上で総和が1になる「確率の数値の表」のみを定式化したに過ぎません。

非自明なのは、確率の数値の表のデータのみから出発して有用な数学的道具が得られることです。

続く
#統計 例えば、公平な通常のサイコロの「確率モデル」は確率の数値の表

1 ↦ 1/6
2 ↦ 1/6
3 ↦ 1/6
4 ↦ 1/6
5 ↦ 1/6
6 ↦ 1/6

によって与えられているとしてよい。σ代数は{1,2,3,4,5,6}の部分集合全体の集合で、確率測度PはA⊂{1,2,3,4,5,6}に対してAに含まれる元の確率の総和を対応させる函数。
#統計 sample spaceが無限集合の場合や、σ-algebraがsample spaceの冪集合でない場合への一般化を素直に行えば、一般的な確率空間の概念ができあがります。続く
#統計 上のサイコロの例から、一般の確率空間に飛ぶのは不親切で、「確率の数値の表」の連続版である確率密度函数についても説明しておいた方が親切でしょう。続く
#統計 数学が苦手な人は、確率空間を与えることは、「確率とは何か」という問題を避けて、単に確率の数値の表(もしくはその連続版の確率密度函数)を与えることに過ぎない、と了解しておけば、変な誤解を防げると思います。

あと、上でのサイコロの例のように具体例を必ず考えておくことも大事。続く
#統計 現実に得られるデータが何らかの確率法則で生成されていると想定することを、確率空間の概念を用いて定式化することは、確率法則を生み出す仕組みには一歳触れずに、「確率の数値の表」(もしくは同類のものの一般化)のみによって定式化することだと思っておけばよいと思います。
#統計 確率空間(単なる「確率の数値の表」の一般化)を考えることと、データの背後にデータを生成した未知の法則を想定することは全然違う話なので、その辺を明瞭に区別するように読者は注意するべきだと思います。

特に数学が得意じゃない人はその点に気をつけるべきです。
#統計 以上において、重要なポイントは「データを生成した未知の法則」という言い方の「未知の」の部分です。

「データを生成した未知の確率法則」を「確率の数値の表」で定式化する場合には、「その数値の表は未知である」と想定する必要があります。

この点もこの本を読むときには要注意な点です。
#統計 以上、長くなってしまいましたが、ツイッターでは繰り返し述べていることを、ここでも繰り返しただけです。

「また、あの話かよ！」と思った人には、ごめんなさい。

他人が書いた本にコメントするふりをして、自分が言いたいことを言うスタイル(笑)
全然先に進まない。

このスレッドの長さは数百オーダーになる予感。
#統計 記号の使い方についての注意

p.27以降ではX,Yをそれぞれ身長と年齢を表す確率変数としています。

一方、p.14では、n人の学生の身長と年齢の標本共分散を Cov(X, Y) と書いています。

読者は、確率変数X,Yの共分散とp.14での標本共分散を混同しないように注意が必要です。続き
#統計 統計学の初学者の多くは

①確率変数達の平均や分散や共分散

と

②標本における平均や分散や共分散

を混同します。

確率空間の定義に「標本空間」という用語が出て来ることもこの混乱を増幅していると思う。

そして何よりも解説している側が十分に慎重になり切れていないことが問題。続く
#統計 「その辺についても分かり易い教科書をお前が書け！」とか言われたりするのは結構悪夢かも(笑)

統計学は色々ややこしいので、致命的にひどい説明をせずにすべてを切り抜けることができると想定することは私には不可能。
#統計 例えば、S市の中学1年生男子の身長について統計分析したいとします。

想定①

S市の中学1年生男子達の身長はすべて確定した数値であると想定し、n人の無作為抽出で身長のデータを得る、という設定を考えるときには、S市の中学1年生男子達全員分の身長の数値は確定しているが未知であり～続く
#統計 続き～、無作為抽出の段階で確率的な選択が導入され、未知の確率法則の定式化として、数値が未知の身長全体の数表から、ランダムにn人分の数値が抽出されたという設定を使えます。

続く
#統計

想定②

S市の中学1年生男子各々の身長が何らかの未知の確率法則によってランダムに決まっていると考えることもできます。この場合には、連続的な未知の確率分布を数学的に想定して、S市の中学1年生男子全員分の身長の数値はその確率分布のサイズNのサンプルになっているのように考える。
#統計 以上の想定①と②では、未知の確率法則の数学的定式化が違っています。さらに別の想定を考えることもできます。(そして、以上の説明で曖昧にすませた部分のギャップを埋めることもできる(笑))

データが未知の確率法則で生成されているという想定自体に無数の可能性がある点にも気をつけるべき。
#統計 p.31にも非常にまずそうな説明の仕方を発見！

さすがに【確率変数が持つ分布を特徴付ける値を、その期待値～という】という言い方は非常にまずい。

確率変数Xの分布はその函数の期待値𝔼(f(X))の全体で特徴付けられる、なら意味が通っていた。

続く Image
#統計 続き。一般に、母平均μ=𝔼(X)や母分散𝔼((X-μ)²)のような有限個の値で確率変数Xの分布は一意に特徴付けられないという点も徹底的に強調するべき重要なポイントです。

なぜならば統計学入門の教科書におけるパラメトリック統計の説明がその点に無頓着である場合が多いからです。
#統計 p.31での期待値に関する非常にまずい説明の仕方の直後のp.31の終わりに2行からその次のページ(添付画像)にかけて、上で私も説明した重要なことが説明されています。

データを生成した未知の確率法則を想定するときの確率法則は未知であるという当たり前の話がやっとここで説明されている。 Image
#統計 この本は説明のまずい点のギャップを埋めずにまともに理解することは不可能な本だと私は思いました。自分で訂正してギャップを埋めて読む人向けの本でしょう。(そういう本は数学の本では結構あります。)
#統計 説明の仕方にまずいところはあっても、この本の著者と私の間では「統計学入門の教科書の解説がひどい」という意見では一致する可能性もあるのではないかと、以上で紹介した部分を見て思いました。

「主観確率」の「ベイズ主義」でベイズ統計について語っている部分が残念です。
#統計 2-2-3節では「データの生成のされ方を未知の分布に従うの独立同分布確率変数列で定式化する」という数学的な扱いが易しくなる設定について説明している。

実践的な統計分析ではそれですまない場合が多いので、私なら「簡単のため」の仮定だと言ってしまいます。続く
続き。脱線。

「簡単のために」という言い方を「我々」はよくするのですが、多くの人がその言い方に違和感を感じて文句を言っている、という面白い話があります。検索すると結構楽しめると思います。

脱線終わり。続く
#統計 本当は、【ヒュームが「自然の斉一性」と呼んだもの】の具体的な内容を独立同分布確率変数列(私は大文字で書くのは嫌いでi.i.d.と略す)のような狭い枠組みに押し込めることが、正しい考え方であるかどうかは、議論があって然るべき点です。

だから私は「簡単のために」と言いたくなる(笑)。
#統計 pp.33-35の2-2-4のポイントは(適当なゆるい条件を満たす)未知の分布に従う長さnの独立同分布確率変数列X_1,…,X_nについては、分布が未知のままであっても、標本平均(←これも確率変数になる)の分布のn→∞での様子について普遍的な数学的法則があることです。
#統計 未知の確率法則を未知だとみなしたままであっても使える普遍的な数学的定理があることが重要。

そういう数学的定理のお陰で、未知の確率法則でデータが生成されているという想定のもとでの、統計的推論・推測・推定が可能になる。

この部分は哲学用語の味付け無しに理解しておくべき部分です。
#統計 もちろん、数学的想定から数学的議論で何が可能であるかをクリアに理解した後に、それを哲学的な味付けのもとで合理的に解釈する自由はあります。

しかし、最初は身もふたもないほどクリアな議論で理解しておくべき重要な事柄。
#統計 pp.35-37での「統計モデル」の説明にコメントする前に、私が繰り返し述べて来た事柄について説明します。続く

(pp.35-37の意味での「統計モデル」はみんなが「統計モデリング」と言う場合の統計モデルとほぼ同じ意味だと思って構いません。この点は「確率モデル」という用語法のまずさとは違う)
#統計 簡単のために(笑)、データは未知の分布q(x)(←確率密度函数)に従う長さnの独立同分布確率変数列として生成されていると想定している場合を考える。

そのときデータ(=長さnの独立同分布確率変数列)の確率密度函数は

q(x_1)…q(x_n)

になり、これがデータの未知の生成法則の定式化になる。続く
#統計 我々は、そのデータの未知の生成法則を推測したい。

その目的のために、分析用のモデルとして既知の確率分布を使って書けるパラメータw付きの確率分布

p(x_1,…,x_n|w)

を用意して使う方法がよく使われています。続く
#統計 想定しているデータの未知の生成法則の確率密度函数は

q(x_1)…q(x_n)

の形(i.i.d.を与える)だが、分析用のモデルの確率密度函数をそれよりも一般的な

p(x_1,…,x_n|w)

の形にしたことは、ベイズ統計の理解では決定的に重要！続く
#統計 続き。なぜならば、ベイズ統計では、パラメータw付きの確率密度函数p(x|w)とパラメータwの確率密度函数φ(w)を具体的に与えて、分析用のモデルの確率密度函数を

p(x_1,…,x_n) = ∫p(x_1|w)…p(x_w)φ(w)dw

の形で与えることが多いからです(簡単のためハイパーパラメータ無しの場合にしてある)。
#統計 分析用のモデル

p(x_1,…,x_n) = ∫p(x_1|w)…p(x_w)φ(w)dw

はもはや、想定していたデータの未知の生成法則

q(x_1)…q(x_n)

とは違って、i.i.d.の確率密度函数にはなっていません。

それにも関わらず数学的に良い性質のお陰でベイズ統計は役に立つことが知られているわけです。続く
#統計 ベイズ統計をまともに理解するためには、想定しているデータの未知の生成法則とは異なる型のモデルを用いることにも数学的合理性があることを数学的に理解する必要があります。

その点を「主観確率」や「ベイズ主義」と言った用語の使用で何とかしようとするとシンプルにアウトになります。続く
#統計 ベイズ統計における分析用のモデル内における仮想的なデータ生成法則の密度函数

p(x_1,…,x_n) = ∫p(x_1|w)…p(x_w)φ(w)dw

におけるパラメータwの確率分布φ(w)はよく事前分布(prior)と呼ばれているものです。役に立てば何でもよくて、主観の表現だと解釈する必要は全くない。続く
#統計 q(x)やp(x|w), φ(w)という記号法は、渡辺澄夫著『ベイズ統計の理論と方法』の記号法をそのまま流用しています。

現時点では、i.i.d.の想定でのベイズ統計の設定について、最もクリアに書かれている教科書なので、是非とも参照して欲しいと思います。
#統計 添付画像に「統計モデル」に関するp.36の説明を引用しておきます。

この部分の説明は結構良いと思いました。

しかし、統計モデルを「確率モデルにさらなる仮定を加え」たものだと説明しているのは、2つの意味で誤解を招きかねないと思いました。続く Image
#統計 1つ目は「確率モデル」という用語法が悪過ぎて、読者が誤解する可能性が高いように思えることです。「確率モデル」と「統計モデル」を区別させるのは苦しい。

略してサボらずに、「データを生成していると想定している未知の確率法則の数学的定式化」のように長くしつこく言えば良いと思う。
#統計 2つ目。「確率モデル」=「データを生成している未知の確率法則に関する想定」にさらに仮定を加えたものを「統計モデル」と呼ぶ方針だと、データを生成している未知の確率法則に関する想定における密度函数

q(x_1)…q(x_n)

と統計モデル内におけるデータ生成法則の密度函数が同じ形で～続く
#統計 続き～、

p(x_1|w)…p(x_n|w)

の形をしていなければいけないかのようになってしまいます。ここでq(x)は未知の確率密度函数で、p(x|w)はパラメータwを持つ既知の確率密度函数です。

このように制限するとベイズ統計の方法が排除されてしまいます。
#統計 想定しているデータの生成法則(未知)には、原理的に決して一致することがないモデル(既知の確率分布で記述)を統計分析用に用いるというアイデアは非常に重要です。
#統計 事前分布の使用はそのアイデアの特殊な場合だし、ベイズ統計の技術を使って、

実際には値が確定していたが値の記録が残らなかったと想定している数値が分析用のモデル内部では確率分布していると考える

という方針もアイデアの特別な場合とみなせます。
#統計 現実に使われている統計学の技術について、クリアな解説を書きたければ、役に立つ統計分析用のモデルは、データを生成していると想定している未知の確率法則にさらに仮定を付け加えてできるものだけではない、と最初から強調しておく必要があります。
#統計 pp.231-236の参考文献には、

* 渡辺澄夫著『ベイズ統計の理論と方法』(2012)

も

* 浜田宏他著『社会科学のためのベイズ統計モデリング』(2019)

のどちらも含まれていない。
#統計 p.30には、確率と確率密度の使い分けにあまり拘らずに

【両者をともに「確率」と統一的に呼ぶことにし、P(X=x)はXが離散の場合は値xの確率、連続の場合はその確率密度を表すことにする】

と書いてあるが、そういう手抜きは読者のためには、やめた方がよかった。pp.38-41を見てそう思った。
#統計 pp.41−42より

データを生成していると想定している未知の分布(本の中では「確率モデル」)における相関係数は母相関係数と呼ぶが、それとは完全に区別するべき統計モデルにおける相関係数はパラメータと呼ぶ方針ではなかったのか？

ここはちょっとひどすぎるかも。 Image
#統計 もう疲れ切ったので、pp.43-49はとばしてしまおう。

コメントするべき部分があると主張したい人は私が見える場所でコメントしてくれると助かります。

とばすことにすれば、次は【第2章　ベイズ統計】です😊
#統計 このスレッドに書いていることは、私がいつもしている話そのものなので、過去の発言をツイログで検索すれば、このスレッド内での説明不足の部分を補える可能性があります。
↓
twilog.org/genkuroki
#統計 もしかして、私はp.36の説明を好意的に読み過ぎている？
#統計 p.36の説明は非常の重要だと思ったので、以下のリンク先で引用しました。
#統計 この本をいち早く購入してすでにツイッターに読んだ感想のスレッドを書いている人がいるが、その感想に理解は伴っているのだろうかと思いました。

このスレッドで紹介した部分の説明が雑なことは明らかで、そういう説明でどれだけの読者が正確に理解できたのだろうか？私には理解不能だった。
#統計 多くに学生が統計学入門の教科書を読んで感じる疑問は、

データを取得した母集団の分布は不明のはずなのに、母集団分布が正規分布になっていると仮定してよいのか？

です。正解はダメに決まっているです。続く
#統計 続き。データを取得した母集団の分布は不明のままとした上で、分析用のモデルとして正規分布モデルを採用すると考えなければいけない。続く
#統計 続き

①データを生成した未知の法則に関する想定

と

②統計分析用に用いるモデル内の想定

は厳密に区別しないとダメです。

①の想定に新たな仮定を加えたものを②の想定だと考えてしまうと、①と②の区別が曖昧になり、非科学的な考え方になってしまいます。
#統計 事前にデータを生成している法則についてよく分かっている場合は違いますが、そうではない一般的な状況においては「データを生成した確率法則は正規分布になっている」とすることには根拠がなさすぎになります。続く
#統計 それに対して、正規分布モデルの妥当性について根拠がないことを知りながら、試しに正規分布モデルを使った推測結果を計算してみるという行為には合理性があります。

推測結果を発表するときにも、正規分布モデルが妥当だという根拠はないと正直に言わなければいけない。続く
#統計 続き。さらに、想定している未知の法則が正規分布からずれていても、分布の近似に関する数学的な根拠によって、正規分布モデルによる推測の誤差が実用的に十分な範囲内に収まる可能性が高いならば、そういうこともしっかり説明しておくべきでしょう。
#統計 続き。実際にコンピュータで数値実験してみると、中心極限定理が効けば誤差が小さくなるような仕組みの推定においては、推定先の未知の分布が正規分布から大きく離れていなければ誤差は小さくなります。
#統計 しかし、推定先の未知の分布が、左右対称形でないせいで、正規分布から大きく離れている場合には、中心極限定理が来にくくなって誤差が許容範囲を超えてしまうことになります。
#統計 各分野の専門家であれば、分野固有の専門知識と以上で述べたような数学の知識を使えば、正規分布モデルを用いた分析の誤差がどういう感じになりそうか大体分かる場合もあると思われます。

誤差が小さくなる公算が高ければ正規分布モデルの使用は科学的に十分合理的だと分かるわけです。
#統計 以上のストーリーでは、「データを生成したと想定している未知の分布が正規分布からずれていたときに、正規分布モデルによる統計分析の結果の誤差がどうなるか？」と考えることができたので、科学的な合理性を保つことができました。
#統計 しかし、正規分布の統計モデルを考えることが「データを生成していると想定している未知の分布は正規分布になっていると仮定すること」ならば、以上のストーリーは最初から起こり得ず、科学的に真っ当な分析への道は閉ざされてしまうことになります。
#統計 以前にも述べたように、以上で述べたような事柄について統計学入門における正規分布の仮定はお寒いものになっています。(具体例として東京大学教養学部統計学教室編『統計学入門』を取り上げた。)
#統計 上のストーリーを一般化を、渡辺澄夫著『ベイズ統計の理論と方法』の記号と用語を使って説明すると、勝手に真の分布q(x)がモデルp(x|w)によってぴったりq(x)=p(x|w₀)の形で書ける(実現可能)と仮定してはいけない、ということ。モデルで真の分布がぴったり実現可能でない場合も考慮するべき。
#統計 一般読者のための資料

データ(サイズnのサンプル)を生成した分布が分析用のモデルで実現できない場合のフィッティングの様子

ソースコード↓
nbviewer.jupyter.org/github/genkuro…

データはガンマ分布で生成
正規分布モデルでフィッティング
#統計

正規分布モデルによるフィッティングは標本平均と標本分散の計算と実質的に同じ。

Laplace分布モデルによるフィッティングは標本の中央値の計算を含む。

標本の代表値の計算は統計モデルと関係有り。

nbviewer.jupyter.org/github/genkuro…

データはガンマ分布で生成
Laplace分布モデルでフィッティング
#統計

動画の右半分は尤度函数のヒートマップです。

nbviewer.jupyter.org/github/genkuro…

データは2つ山の混合ガンマ分布で生成
単なるガンマ分布モデルでフィッティング
#統計 以上で用いた統計モデルは指数型分布族なので、特に常に正則モデルになります。サンプルサイズnを大きくしていくと、尤度函数の形は多変量正規分布に近付き、尤度函数の台もどんどん小さくなって行く。

こういうことは正則モデルでは普遍的に起こる。
これが最尤法の数学的基礎です。
#統計 より実践的な例。添付画像は論文

pubmed.ncbi.nlm.nih.gov/32046819/

での新型コロナの潜伏期間の推定を同じ方法で行なってプロットした予測分布。論文にはないグラフ。

3種類のモデルを試している。私がWAICを計算したら値に大きな違いはなく、優劣は付けられなかった。

nbviewer.jupyter.org/gist/genkuroki… Image
#統計 実践的な統計分析では、データを生成していると想定している法則をモデルがほぼぴったり実現しているとは仮定できそうもない場合が多い。

分析用のモデルを複数種類試してみるなどの方法で、推測結果がモデルの詳細に大きく依存し過ぎないことやどのモデルがもっともらしいかの確認が必要。
#統計

東京大学教養学部統計学教室編『統計学入門』
【事前に母集団分布が××分布という形で与えられており、いくつかの定数がわかれば、母集団分布についてすべてを知ることができる場合、それをパラメトリックの場合と呼ぶ】

この説明の仕方は非常にまずい。
#統計 現実の統計分析は「真実は闇の中」になることが多いと思う。

複数のモデルの比較は情報量規準などで一応可能だが、データを生成していると想定している法則がモデルでどの程度近似できているかはよくわからず、分野固有の知識を持っている専門家による精査がないと怖くて使えない感じ。
#統計 上で紹介した論文の新型コロナの潜伏期間の推定の再現を #Julia言語 のTuring.jlを使って行った結果をツイッターで紹介するときには緊張する。

なぜならば、私は完全など素人であり、責任を持てるような専門知識が皆無だからだ。私が再現した潜伏期間の推定が大外ししている可能性が怖い。
#統計 解説：グラフはモデル内での潜伏期間の分布の密度函数のプロットです。

原論文と同様にベイズ統計を使っていますが、「主観確率」の「ベイズ主義」に基くベイズ統計は使っていません(笑)。信念がベイズ更新されたりもしていない(笑)。
#統計 以下のリンク先の発言もこのスレッドに収録しておく。
#統計 『統計学を哲学する』のp.31の引用の再掲

私はまだp.42までとp.91にしか目を通していないのだが、その中ではこのページが最もひどい。

この本の著者は「期待値」の標準的な意味を理解していない。 Image
#統計 真っ当な人がレビューしていてくれれば、p.31のような非常識な説明が生き残る可能性はなかったはず。さすがに

【確率変数が持つ分布を特徴付ける値を、その期待値～という】

という説明はまずすぎる。

せめて「期待値」の標準的な定義を理解してから本を書くべきであった。 Image
#統計 この本は大人気のようだが、他人にこの本を勧めるときには、この本に【確率変数が持つ分布を特徴付ける値を、その期待値～という】(p.31)と書いてあることを注意するくらいの親切心があった方がよいと思う。

期待値の普通の定義くらいみんな知っているだろうから、容易に指摘できるはず。
#統計 雑談：分布を特徴付ける数値の組は普通パラメータと呼ばれる。

指数型分布族(←例: 正規分布、ガンマ分布、Poisson分布、二項分布など)のパラメータが分布に従う確率変数の具体的な函数の期待値で表されることは面白い話です。

続く
#統計 統計モデリングでビルディングブロックの役目を果たすことが多い指数型分布族の確率分布は統計力学の意味でのカノニカル分布として自然に現れ、カノニカル分布の一般化の仕組みを理解していれば、逆温度の一般化である指数型分布族のパラメータが期待値で特徴付けられることも自然に理解可能。
#統計 i.i.d.の場合のカノニカル分布の理論については、私のノートで結構詳しく解説されています↓

genkuroki.github.io/documents/2016…
Kullback-Leibler 情報量と Sanov の定理

* 大数の法則
* 中心極限定理
* Sanovの定理

は統計学における確率論の「三種の神器」。Sanovの定理は通常解説されていない。
#統計 具体例はコンピュータでかなり容易に作れます。

nbviewer.jupyter.org/gist/genkuroki…
統計力学におけるカノニカル分布の最も簡単な場合 (#Julia言語)

添付動画は X と √X の期待値で特徴付けられる一般化されたカノニカル分布をMCMC法で作る様子の動画。
#統計 正値の確率変数Xについて、Xと√Xの期待値で特徴付けられる一般化されたカノニカルの台はx>0で密度函数は

定数×exp(-ax+b√x)

の形で、ガンマ分布などに似た形の分布になります。パラメータのaとbが逆温度の一般化になっている。

こういう話は非常に面白いです。
#統計 この本には【確率変数が持つ分布を特徴付ける値を、その期待値～という】(p.31)などと書かれていると指摘しても、本を購入していない人にとってはどうでもよいくだらない話にしか聞こえないだろうと予想して、くだらなくない真に面白い話を雑談として紹介しているつもり。
#統計 添付動画は一般化されたカノニカル分布としてのガンマ分布の実現の様子です。正値確率変数Xに関するXとlog(X)の期待値でガンマ分布は特徴付けられます。

ガンマ分布のパラメータの推定値はサンプルの相加平均と相乗平均から得られます。続く

nbviewer.jupyter.org/gist/genkuroki…
#統計 サンプルX_1,…,X_nの相加平均は通常の標本平均で、相乗平均の対数は

log(X_1…X_n)^{1/n} = (log(X_1)+…+log(X_n))/n

とサンプルの対数平均になります。これのn→∞での極限は大数の法則よりlog(X)の期待値なる。

相加・相乗平均が出て来ることはガンマ分布の基本的な特徴です。続く
#統計 ガンマ分布の台はx>0で密度函数は

定数×exp(-ax+b log(x))

の形で、a,bが逆温度の一般化のパラメータで、xとlog(x)の期待値でパラメータが特徴付けられます。

ガンマ分布におけるlog(x)の期待値は本質的にディガンマ函数で、コンピュータで容易に計算できる基本特殊函数の1つになっています。
#統計 正規分布の密度函数は

定数×exp(-ax²+bx)

の形でX²とXの期待値でパラメータa,bが特徴付けられます。

一般に一般化されたカノニカル分布=指数型分布族の密度函数は

定数×exp(-Σ_i a_i f_i(x))q(x)

の形でパラメータa_i達は𝔼[f_i(X)]達で特徴付けられる。
#統計 以上を読めば、たとえすぐに詳細を理解できなくても、統計モデリングのビルディングブロックとして使われる指数型分布族の確率分布のパラメータの特徴づけの基本パターンと、統計力学におけるカノニカル分布の関係を理解することが、結構基本的であることを想像できると思います。
#統計 以上で述べた一連の「雑談」の内容は、コンピュータを使った最も優しいMCMC法の演習としても価値があります。

数学的一般論によって収束先の分布がどうなるかを知っていても、コンピュータで再現できると理解が進みます。

添付動画は収束先が正規分布の場合。
#統計 注意

* これは中心極限定理の動画では__ない__。

* 正規分布の密度函数の定数倍を使ったMCMC法の動画でも__ない__。

* カノニカル分布としての正規分布を分布のランダムウォークで実現する動画で__ある__。

nbviewer.jupyter.org/gist/genkuroki…
#統計 一般に分布q(x)に付随する一般化されたカノニカル分布(=指数型分布族)

定数×exp(-Σ_i a_i f_i(x))q(x)

は期待値達𝔼[f_i(X)]の値が与えられたときの「もっともありがちな分布」として特徴付けられます。

これは統計モデリングで適切そうな指数型分布族の選択でヒントになりえる情報だと思う。
#統計 適当に動ける範囲に制限を付けて分布をランダムウォークさせたときの収束先の分布は、その制限の範囲に含まれる分布の中でもっともありがちな分布であるということになります。

ランダムウォークで適当に制限された範囲で最もありがちな分賦を探索している様子の動画↓
#統計 ソースコード nbviewer.jupyter.org/gist/genkuroki… も全公開しているので、自分で以上のような計算をコンピュータにやらせたい人はいつでも「答えのコード」を閲覧することができます。

この手の計算に #Julia言語 は非常に向いています。
#統計 件の本のp.47の図1.4のように

math.wm.edu/~leemis/2008am…

から添付画像の部分を引用しても、各種の分布の理解に役に立つことはありません。

統計モデリングでのビルディングブロックになるような確率分布の理解はそういうものではありません。

私がしている雑談に近い試行錯誤が重要です。 Image
#統計 p.49の読書案内によれば、私ならば読者の理解という観点からふざけた態度だと判定するp.47の図1.4への1つ前のツイートの添付画像の部分の引用は【三中本からの孫引き】らしい。

一般にまるで曼荼羅に見える複雑な図を引用したがる人は要注意だと私は思います。自分で作った図でさえない。
関連
他人が作った曼荼羅っぽい図を引用したりせずに、自分の試行錯誤の結果を図にまとめないとダメ。

そして真に意味のある試行錯誤をしていれば、網羅的な曼荼羅図が出来上がることは決してないと思う。
#統計 関連
#統計 事前分布については、以下に引用するように考えておけばよい。

gamp.ameblo.jp/yusaku-ohkubo/…
【・事前分布はRIdge回帰やLASSO回帰のように推定値を安定化させるための道具であり、主観的な事前の信念を反映させるものではない
・事前分布は、事後予測分布などを通じて客観的に評価可能である】
#統計 事前分布を単なる数学的道具とみなせるだけの知識がないせいで、事前分布を「事前の主観的な確信の度合い」のように解釈するのは無知すぎます。

事前分布の適切な利用によって平均予測誤差を小さくしたりできるから、事前分布はデータサイエンスで重要な道具の1つになっています。
#統計 前もってどの事前分布を利用するべきであるか分からない場合であっても、情報量規準や交差検証などによって、どの事前分布が相対的に優れている可能性が高いかを見積もることもできる。

事前分布を主観確率で解釈している人達はどんだけ知識をアップデートしていないのやら。
#統計 このスレッドで話題にしている『統計学を哲学する』の「第2章　ベイズ統計」はストレートに太古の時代の「主観確率」の「ベイズ主義」の話が書いてありました。

渡辺澄夫著『ベイズ統計の理論と方法』のような現在では定番の教科書さえ目を通していないのだと思いました。
#統計 この本には【確率変数が持つ分布を特徴付ける値を、その期待値～という】(p.31)と本当に書いてあります‼️

そういう著者に渡辺澄夫著『ベイズ統計の理論と方法』のような本を勧めるのは無茶かもしれませんが、数式ではなく、言葉で説明してある部分だけでも理解できれば全然違っていたと思う。
#統計 ベイズ統計の技術を使えば、今までオーバーフィッティングが原因で不可能だった推定が可能になりだろう的な話は40年前の赤池弘次さんの論説にも書いてあります。

ismrepo.ism.ac.jp/index.php?acti…
統計的推論のパラダイムの変遷について(1980)
の第6節を参照
#統計 赤池さんは正しかった。

渡辺澄夫著『ベイズ統計の理論と方法』では、最尤法が有効でない場合であっても、ベイズ統計ならば良い性質を持つことが示されています。

そういう数学的な良い性質に触れずに、「主観確率」の「ベイズ主義」にベイズ統計を落とし込むのは無知丸出しでまずすぎます。
#統計 統計学に限らず、多くの技術は時代とともに進歩して行きます。そういう技術について「哲学」を語るときには、可能な限りその時代の技術水準に追いついて、おかしなことを言わないように気をつけるべきです。

この本の第2章はそういう意味では完全に失格。
#統計 多くの誤解もしくは時代遅れに考え方が広く普及してしまっている現代では、ベイズ統計に関する解説では真っ先に「主観確率のベイズ主義は現代のベイズ統計においては無用のものになっている」と説明するべきです。
#統計 そして、データサイエンスにも関係している話をしたければ、リッジ正則化やLASSO正則化の話に触れて、そこから事前分布の使用が平均予測誤差を下げるために役に立ちそうな道具であることに触れて、事前分布を事前の主観の表現とみなす考え方が本当に無用になっていることを説明するべき。
#統計 そしてできれば、21世紀の研究である渡辺澄夫さんの仕事に触れて、ベイズ統計ならば特異モデルになる可能性がある構造を持った複雑なモデルであっても(最尤法と違って)良い性質を持つことが示されていることにも言及した方がよいと思う。
#統計 そして、一般の場合の(i.i.d.を仮定しない場合の)ベイズ統計の性質はまだ十分に分かっていないというようなことにも触れた方がよいと思う。

我々はすでに何でも知っているわけではないという認識は非常に重要だと思います。
#統計 ベイズ統計入門

未知の確率分布を持つサイコロXの出目の確率を「確率分布は添付画像のサイコロA,B,Cのどれかである」というモデルを使って推定してみよう。

サイコロAは1,2が、Bは3,4が、Cは5,6が出易いイカサマのサイコロのモデル化である。続く Image
#統計 ケース1

事前分布として、サイコロA,B,Cの確率はどれも1/3を設定し、サイコロXを何度も振って出た目を使ってベイズ更新を行う。

添付動画はそのベイズ更新の様子である。出目の割合を表す赤のドットの動きを見ると、サイコロXの確率分布はモデルのサイコロA,B,Cのどれとも違うっぽい。続く
#統計 ケース1つ続き

実はこのケース1でのサイコロXはイカサマでないすべての目がどう確率で出るサイコロである。

この場合にはサンプルサイズ→∞でベイズ更新は収束せず、推定結果は決して真実に到達しない。
#統計 ケース2

このケース2のサイコロXはケース1のそれとは異なる。

ケース2におけるベイズ更新の結果はモデルのサイコロBに収束している。

しかし、出目の割合の赤のドットを見ると、このケース2のサイコロXはベイズ 更新の収束先のサイコロBとは違うっぽい。
#統計 ケース2続き

実はこのケース2におけるサイコロXでは3の目だけが他の目よりも出る確率が少しだけ高い。

この場合には、ベイズ更新はモデルの範囲内で真実を最もよく近似する分布(サイコロB)に収束するが、決して真実にはたどりつかない。
#統計 ケース2のように、ベイズ更新の結果がモデルの範囲内で真実を最もよく近位する分布に収束することは、非常に一般的にかなり緩い仮定のもとで示せます。

サンプルサイズ→∞で、モデルの限界まで推測の精度は上がりますが、それを超えて精度が上がることはない。
#統計 ところが『統計学を哲学する』p.83(添付画像)には、まるでモデルの分布族で実際のデータ生成プロセスを全然表現できない場合であっても【ベイズ流の更新のプロセスは最終的に真理に到達しうる】と書いてある‼️

これなに？

ベイズ統計を全然わかっていないように私には見えた。 Image
#統計 分析用の統計モデルが実際のデータ生成プロセスを全然表現できないのに、そのモデルを使って真理に到達できるはずがない。そういう魔法のようなことがベイズ 統計なら原理的に可能だと本気で信じているとしたら、相当にどうかしていると思いました。
#統計 この本の著者は「期待値」について【確率変数が持つ分布を特徴付ける値を、その期待値～という】(p.31)と説明してしまうくらいなので、数学的な技術的な事柄に関する説明は全く信用できず、引用している文献を参照する手間をかける気には全くなれない。
#統計 正直な感想として、ページをめくるたびに次々に襲いかかってくるいかにもまずそうな説明が苦痛な本だと思いました。

さらに先を読めばどこかに価値あることが書いてあるのでしょうか？

めちゃくちゃ辛い。
#統計 以下のリンク先(このスレッドのちょっと上)にある動画を作るためのソースコードは

nbviewer.jupyter.org/gist/genkuroki…

においてあります。このスレッドで使っていない動画もそこで閲覧できます。ベイズ更新の様子を直観的に理解するために有用だと思います。
#統計 厳しい言い方をしていますが、純粋に「つらい気持ち」を表現しているだけで、他意はないです。

この長大なスレッドでは、より真っ当な理解に至るために必要な資料(私自身が作った動画を含む)を可能な限り紹介するように努力しました。そういう方向の努力が実れば一番うれしいです。
#統計 以下のリンク先の引用は、以下のリンク先のリンク先における

stat.columbia.edu/~gelman/resear…
Philosophy and the practice of Bayesian statistics Andrew Gelman and Shalizi
2012

の紹介からの孫引きです。この論文は『統計学を哲学する』でも引用されています(pp.84-87)。続く
#統計 しかし、

ameblo.jp/yusaku-ohkubo/…
【事前分布は～主観的な事前の信念を反映させるものではない】

という実践データサイエンス的には普通の考え方を受け入れておらず、「信念」という解釈を捨てていない。

「主観確率」「信念」という解釈が無用であることを理解できないようだ。
#統計 『統計学を哲学する』に限らず、現在では無用になっている「主観確率」の「ベイズ主義」に基くベイズ統計の解釈を捨てられない困った人達は、ベイズ統計の説明で実践的にはベイズ統計が使われそうもない単純な統計モデルで説明しようとする傾向が強い。続く
#統計 続き。よく見るのは、ベルヌーイ分布モデル(コインを投げたとき表の出る確率がpである場合のモデル化)です。

「主観確率」論者にとってそういう単純なモデルで説明することには大きなメリットがあります。「表の出る確率pとして何がもっともらしいと事前に思っているか」という話をし易い！続く
#統計 ベイズ統計の技術が有効になりそうな数学的に複雑なモデルだと、直観が効かなくなるので、主観を事前分布に反映させる話をし難くなるのです。

それは「主観確率」でベイズ統計を説明したい人にとっては非常に不都合です。続く
#統計 さらに説明用のモデルが、実際に使用されているようなモデルだったりすると、実際に使用されている事前分布が「主観」「信念」「確信」の類とは全然違う規準で決められているという事実を指摘される可能性が高まるので、さらに都合がわるいでしょう。
#統計 ベルヌーイ分布モデルは「主観確率」でベイズ統計について説明したい人にとっては非常に都合のよい単純な統計モデルだと言えます。

「主観確率」とか言わない真っ当な人達は、階層ベイズのようなちょっと複雑なモデルを例に使うことが多いと思う。
#統計 実際にベイズ統計の計算を試してみると、単純なモデルなら最尤法でやってもおとなしめの任意の事前分布でベイズ統計を使っても得られる結果はほぼ同じになることも多く、そうでなくても事前分布のちょっとした違いよりもモデル全体の設定の方が結果に与える影響が大きかったります。
#統計 さらに、最尤法で分析してもよいことを知りながら、複雑なモデルを回すのが楽なベイズ統計の側を使うこともある。

ベイズ統計になった途端に「主観確率」の「ベイズ主義」が必要になるなどと考えていたら、自由に統計分析できなくなってしまいます。
#統計 訂正版

「8割おじさん」として有名になった西浦博さん達による分析のリポジトリを見ると、最尤法とベイズ統計の両方を同じように使っています。

8割おじさん達が最尤法ではなくベイズ統計を使ったときにのみ信念を更新しているとは思えません(笑)
#統計 8割おじさん達が公開しているリポジトリは

github.com/contactmodel/C…

にあり、

github.com/contactmodel/C…

には最尤法とベイズ統計(Stan)を使っているJupyter notebooksが置いてあります。どちらのノートブックでも R_t を推定している。
#統計 最尤法でもできることを、ベイズ統計でもやる、というのは分析法をちょっと変えただけで結果が致命的なほど大きく変わらないことの確認には有効だった可能性があります。

ベイズ統計を使った途端に「主観確率」の更新をやっていると思うようになるというのはちょっとあり得ません。
#統計 p.31への書き込みを増やした。さすがに

【確率変数が持つ分布を特徴付ける値を、その期待値～という】

という説明はさすがにアウト。

あと、確率変数が従う分布はデータを取得した母集団分布とは限らないので、その平均(=期待値)と分散を【母平均】【母分散】と呼ぶのもダメです。 Image
#統計 カギカッコ付きの「中心」を使った説明もまずいです。カギカッコに「厳密にはは中心ではないのだが」というニュアンスを込めたと忖度して欲しいのかもしれませんが、そういうことはやめた方がよかった。

このページの態度は多くの読者を落胆させることでしょう。 Image
#統計 統計学における様々な概念について語る場合には

①データを生成していると想定している未知の確率分布

と

②統計分析用のモデル内の確率分布

の厳密な区別が必要です。①における確率変数と②における確率変数が同時に必要な場合があるので、その辺の区別に神経質になった方がよいです。
#統計 上の①と②を区別しているつもりであっても、①の確率分布を既知の確率分布に特殊化したものが②であるかのように思っているとしたら、完全にアウトです。

①の分布を未知のまま放置した上で、②の確率分布を正規分布にしたりするのが正しい考え方です。
#統計 この本では概念的に重要な事柄について驚くほど杜撰な言葉遣いで説明されています。

既出の例の他にも、最尤法について【データを最も良く予測するようなモデルのパラメータを求める】と「予測」という言葉を使って説明していることにはあきれた。続く Image
#統計 「そのデータと同じ数値がモデル内で発生する確率が最大になるようなパラメータを求める」とか、「そのデータにモデルが最も適合するようなパラメータを求める」のようにより正確に書くべき。

「予測」という言葉は重要なので使うべきではなかった。 Image
#統計 あと、最尤法の他にも最小二乗法があるかのように述べているが、最小二乗法は最尤法の特別な場合(残差を期待値ゼロの正規分布でモデル化した場合の最尤法)である。 Image
#統計 添付画像の青線の部分は非常によくない。

ベイズ統計では、分析用のモデル内(モデルは事前分布も含む)での仮説の正しい確率は定義できるが、そのモデル自身の正しさや適切さは別に扱う必要がある。

この点は最尤法とベイズ統計のあいだで違いはない。続く Image
#統計 さらに、最尤法とベイズ統計は近似的にほぼ同じ結果を与えることが相当に沢山あり、正則モデルを使ったi.i.d.のデータを使った推測に限定すれば、サンプルサイズを十分大きくすれば、最尤法とベイズ統計はほぼ同じ結果を常に与えることも証明できる。
#統計 このように、最尤法とベイズ統計は互いにライバル関係にあり、結果を比較可能な分析方法であり、ある場合にはほぼ同じ結果を与えることがわかっている。

そのようなもの達を完全に分断して別物であるかのようにせつめいするのは非常にまずい。
#統計 さらに、最尤法と仮説検定の間はものすごく密接な関係がある。

沢山の種類があるχ²検定の基礎は最尤法について普遍的に成立しているWilks' theoremである。

最尤法とベイズ統計、最尤法と仮設検定の間の関係を理解していないと統計学をスムーズに使うことが難しくなってしまう。
#統計 沢山あるχ²検定と最尤法におけるAICを使ったモデル選択のあいだにも密接な関係がある。

* 仮説検定におけるχ²検定
* 最尤法とAIC
* ベイズ統計とWAIC

は相当に近い関係にあり、コンピュータでそれらの関係を数値的に確認することは良い練習問題になる。
#統計 最も簡単な統計モデルであるベルヌーイ分布モデルの場合の

* 最尤法のAIC
* ベイズ統計のWAICとLOOCV(一個抜き出し交差検証)
* BICと自由エネルギー

などに関するまとめが

nbviewer.jupyter.org/gist/genkuroki…

にある。最尤法とベイズ統計の違いはこの場合には小さい。
#統計 『統計学を哲学する』という本は読者を以下の事柄について正しく適切に考えることから遠ざけるように書かれているので読者は注意した方が良い。社会的には負の業績。

* 期待値
* ベイズ統計
* 最尤法
* 最小二乗法
* 最尤法とベイズ統計と仮設検定の関係
などなど

本当に気を付けた方が良い。
#統計 特に統計学では

* 定義が全然違っている複数のモノが、ある種の状況において、無視できる違いを除いて一致する場合があること

に注意する必要があります。そういう場合には定義が違っていて、概念的には大きく異なるモノであっても、ある種の状況では実質的に同じものとして扱う必要がある。
#統計 そのようなことが、最尤法、ベイズ法、仮説検定の間に成立している場合があるのです。概念的に異なっていたり、定義が全然違っていたり、目的も全然違っていたりしても、ある種の状況では互いに相手を近似しあっており、そのような場合には「違いはない」と言う必要が出て来ます。
#統計 思想や概念や定義の違いよりも、近似的に等しいという数学的な関係の方を優先して考えないと、実質的に同じモノを使っているのに、思想や概念た定義が違うという理由で異なる結論を出してしまう誤りを犯してしまいます。
#統計 関連

1つ前のツイートに関連した滑稽話に以下のリンク先の件がある。
#統計 仮説検定、最尤法、ベイズ法などなどに異なる思想や主義があるかのように考えてしまうのは、単にそれらの数学的関係を理解していないからだと思う。

数学的道具は個々の性質や道具感の関係を数学的に理解した上で、自分の目的に合わせて自由に使えば良い。
#統計 多くの仮説検定は、実質的にパラメータ空間W₁を持つモデルM₁とそれを次元が下がったパラメータ部分空間W₀に制限したモデルM₀の間の比較になっている。

例えば、ベルヌーイ分布モデルでの帰無仮説p=1/2の両側検定は、W₁=[0,1]とW₀={1/2}のデータを用いた比較になっている。
#統計 次元の低いW₀の側が帰無仮説を表している。

そういう比較をdim W₁ = d₁ > d₀ = dim W₀で行う場合のχ²検定の自由度は次元の差d₁ - d₀になる。そのことは最尤法での対数尤度比の漸近挙動に関するWilks' theoremから得られる。
#統計 そういう仮説検定の状況では

* 対数尤度比 = 対数尤度の差
* AICの差 = 対数尤度の差+定数

なのでAICとももろに関係がある。
#統計 仮説検定、最尤法、ベイズ統計の間には、それらを断絶させる深い谷は存在せず、すべてが地続きになっており、何もかも普通に関係しているクリスタルクリアな世界が広がっている。

このような理解を目指すべき。
#統計 最小二乗法は

p(y|X,β,σ²) = (1/(2πσ²)^{n/2})exp(-||y - Xβ||²/(2σ²))

におけるパラメータβ,σ²に関する最尤法。Xは計画行列。
#統計 関連情報

なるほど。「客観ベイズ」も否定しておくのは良いことですね。

あと、最初に試す事前分布は適切な意味で「おとなしめの事前分布」がよいと私も思っています。それでダメなら「狭い事前分布」も試してみる。
#統計 少なくとも、Jeffreys priorを特異モデルの場合に使うと予測誤差(汎化誤差)が悪化するというようなことは知っておくべきことだと思う。

幾何的に定義される座標不変なJeffreys事前分布がダメな場合もある。

watanabe-www.math.dis.titech.ac.jp/users/swatanab…
#統計 あと「パラメータを増やしてモデルがデータにフィットするように調節する」のと本質的に同じことを手動で行っても、オーバーフィッティングで予測誤差が悪化することがあるというような注意も重要だと思う。これはベイズ統計でも同じ。
#統計 1つ前に述べたことは、最尤法の場合に限れば当たり前。

①パラメータを増やす。
②モデルがデータに適合するパラメータを求める。
③求めたパラメータを含むパラメータ数が少ないモデルを作る。
④上の③のモデルのAICを計算。

これ「不正行為」になります。
ベイズ統計でやっても「不正行為」
#統計 基本的に、データを見た後で、モデルの側を色々変えてモデルがデータにぴったり適合するようにがんばると、オーバーフィッティングさせまくることになるので注意。

データを見て適切そうなモデルを探しまくった場合には、別のデータでそのモデルを検証することが必要になる。
#統計 「尤度=モデル内でデータと同じ数値が生成される確率(密度)は、モデルのもっともらしさの指標ではなく、モデルのデータへの適合度の指標に過ぎない」と強調することの背景には、データにぴったりフィットさせようとすることが予測誤差を悪化させるということがある。
#統計 「データを生成していると想定される未知の確率法則がある」という設定で統計分析する場合には、データそのものではなく、未知の確率法則が推測先のターゲットになる。

モデルをデータにぴったりフィットさせることは有害な目標設定になる。
#統計 私的なオーバーフィッティングの大雑把な定義：モデルのデータへの適合度の上昇と予測精度の劣化が同時に進行すること。

添付動画の右側の青線が予測誤差で赤線がデータへの適合度です。赤線下降と青線上昇が同時に起こっているときに過学習が起こっている。

nbviewer.jupyter.org/gist/genkuroki…
#統計 モデルをデータに適合させるパラメータの探索では、最初のうちはモデルのデータへの適合度と予測精度が同時に上昇するが、その後は、パラメータ探索がデータの新しい構造を発見してモデルのデータへの適合度が上昇するときに予測精度の劣化が同時起こるというようなことが起こる。
#統計 データから構造を読み取ってそれをモデルに反映させるごとに、予測精度がその分だけ__悪化__して行く数値例を自分で作って楽しむことは、複数通りの意味で極めて教育的だと思う。

コンピュータではなく、自分自身もデータから構造を読み取って予測を悪化させてしまうかもしれない！
#統計 ちなみに「経験ベイズ」というのも、モデルがデータに適合するようなパラメータ調節の一種に過ぎません。

一般に「〇〇ベイズ」という用語を見たら、歴史的偶然によって広まってしまったが、別の言い方で言い直した方がよい言葉の典型例、とみなしておけばそう間違いがないと思います。
#統計 ベイズ統計のモデル内におけるパラメータη付きの確率密度函数

p(x_1,…,x_n|η) = ∫ p(x_1|θ)…p(x_n|θ)φ(θ|η) dθ
(φ(θ|η)はパラメータη付きの事前分布)

のデータX_1,…,X_nに関する尤度

L(η)=p(X_1,…,X_n|η)

を最大化するようにパラメータηの値を調節するのが、所謂「経験ベイズ」です。
#統計 「経験ベイズ」は以上で述べたようなモノに過ぎないのに、『統計学を哲学する』のpp.79-82には、初めて「経験ベイズ」という用語を知った人にとって適切とは思えない解説が書かれている。

「主観確率」の「ベイズ主義」抜きにベイズ統計について正確に考えることを知らないからそうなる。
#統計 「経験ベイズ」も「モデルをデータにフィットさせるためのパラメータ調節」に過ぎず、その使用者がどのような主義や思想を持っていても、それとは無関係に、モデルをデータにフィットさせるためのパラメータ調節一般で生じることが数学的に生じる。
#統計 通常の議論では、主義や思想と無関係に決まっていること(典型例は数学的にどうなっているか)を明らかにして行くことを優先し、その過程で発見された主義や思想に依存することを別に取り上げる。

そういう慎重な手続きが欠けている本を読むときには注意が必要である。
#統計 例えば、最尤法とベイズ統計や仮説検定の関係について説明する場合には、まず、主義や思想とは独立に、それらの間に数学的に(特に解析学的に)どのような関係があるかを明確にしておく慎重さが必要である。そして、主義や思想について語る場合にはそういう数学的結果に矛盾しないようにするべき。
関連
#統計 渡辺澄夫著『ベイズ統計の理論と方法』のpp.80-82では、分散1の正規分布モデル(パラメータは1つ)と標準正規分布モデル(パラメータ無し)に関するAIC, BIC, 尤度比検定を比較しています。

最尤法、ベイズ、仮説検定の関係の一例がそこにある。
#統計 渡辺澄夫さんが解説しているその例で起こっていることは、数学的に非常に一般的に起こっています。数学的に、最尤法、ベイズ統計、仮説検定は互いに密接に関係している。

ベルヌーイ分布モデルの場合については私のノート(既出)

nbviewer.jupyter.org/gist/genkuroki…

を参照。WAICやWBICも扱われている。
#統計 最小二乗法は単なる直交射影の線形代数にしか見えないのだが(実際にはそのように見えるほど数学を理解していない人の方が多数派)、正規分布モデルの最尤法の一種になっているという認識は実践的な統計モデリングを行う場合には必須の教養のうちの1つ。

こういう点にも雑であってはいけない。
#統計 このスレッドで指摘している『統計学を哲学する』の杜撰な説明の仕方を見れば、この本を統計学における考え方についての教養を身に付けるための本として他人に勧めるのは非常にまずいことが分かると思う。

すでに勧めてしまった人はそれを撤回した方がよい
#統計 繰り返しになるが、【確率変数が持つ分布を特徴付ける値を、その期待値～という】(p.31)という説明の仕方はひどすぎる。

統計学の文脈では「確率分布を特徴づけるパラメータ」という言い方が頻出なのでめちゃくちゃまずい。

確率分布を特徴づけるパラメータを検索↓
google.com/search?sxsrf=A… Image
#統計 添付画像はすでに引用済みのp.36の脚注部分。そこでは

　　　　【母数＝期待値】

という書き方がされていた‼️

確率分布の平均や分散は期待値で表せるが、中央値はそうではない(一意に決まらない場合もある)。

集団の様子を要約するための数値は必ずしも期待値の形になっているとは限らない。 Image
#統計 統計学における母数という用語の使い方は混乱している場合がある。

データが未知の母集団分布からの無作為抽出で得られていると想定しているときに、その母集団分布は平均や分散といった量でパラメトライズされているわけではないのに、母平均や母分散を母数(パラメータ)と呼ぶことがある。続く
#統計 個人的には(おそらく私以外の多くの数学ユーザーは)、パラメータ付き確率分布のパラメータのみをパラメータと呼び、パラメータ付きではない確定した母集団分布の平均や分散をパラメータ(母数)とは呼びたくない。

母集団分布の平均や分散は母集団分布をパラメトライズしたりしていない！続く
#統計 その辺を誤解し難いように整理するためには

* 母集団分布の平均や分散を決してパラメータとは呼ばない。

* 「母数」という言い方も使わない。

* 確率分布族をパラメトライズしている変数はパラメータと呼ぶ。

とするとよいと思う。

あと、「母数=期待値」などと決して書かない(笑) Image
#統計 確率分布族のパラメータ達はその族に入れた座標系なのですが、指数型分布族の場合にはパラメータ達をその分布に従う確率変数の函数の期待値達で与えることができます。これは指数型分布族についての基本の1つ。

パラメータと期待値の関係について語りたければこういう話をクリアにすればよい。
#統計 最悪なのは、未知の母集団分布だったはずのものを、勝手に既知の確率分布族のパラメータが特別な場合、例えば正規分布の特別な場合で置き換えて、母集団分布の平均や分散をパラメータと呼び、パラメータの意味を曖昧にしてしまうこと。

これをやらかすと一挙に非科学的なスタイルになる。
#統計 『統計学を哲学する』は間違い探しで楽しむ本になることを覚悟して購入した方がよい。

この本の著者は「色々わかっていない」という印象がどんどん強くなって来る。

【「Major axes」と表示されているのが回帰直線。】(p.17, 図1.1)

見逃していたので追加。色々ずさん。 Image
個人的には次世代の学生に被害が及ばないか心配。

金銭および知識の両面で。

『統計学を哲学する』を他人に勧めた人達が本当にこの本の内容を理解して読んだとはとても思えない。

目を通してキーワードを拾っただけの印象で他人に勧めたんじゃないか？
#統計 「頻度主義vs.ベイズ主義」の対立を煽っていなくても、21世紀現在数学的に分かっていることを使った整理を十分にすることなく、「主観確率」だの「ベイズ主義」だのがベイズ統計の理解に必須であるかのように語ること自体が有害。

必須ではないことを最初に明瞭に認めるくらいのことは必要。
#統計 あと、議論では必ず例を使って説明することが大事。現代ではStanなどの道具を使っている様子を公開している人達を比較的容易に発見できます。

「主観確率」「ベイズ主義」とか言いたい人はそこで使われているベイズ統計をそれらの用語を使って解釈して見せることが必要。
#統計 このスレッドでも幾つか実践的な事例を紹介していますが、「主観確率」やら「ベイズ主義」とやらは実践的なベイズ統計の応用例を理解するためには何も役に立たず、わたしには完全に無用なものに見える。

誰ならば、Stanを使って(笑)、信念をベイズ更新しているとみなさないと困るのやら。
#統計 実践的には「階層モデルの正しい情報量基準や1個抜き出し交差検証の計算の仕方」の知識は役に立ちます。

結構多くの研究者が既存のライブラリの安易な適用で済ませているせいで、間違った使い方をしている疑いを私は持っています。

深刻な問題ですが、調査が大変なので手を出していない。
#統計 あと、他人がMCMCを回して得た結果を自分でも再現できるかどうかを試してみるのは結構ためになります。

ぴったり再現できる場合は稀で、ちょっとした条件の違いで結果がどう変わるかが見える(笑)

実は他人による再現の試みを見るだけでも相当にためになる。
#統計 そして、各分野の専門家が持っている固有の知識が決定的に重要そうなことにも気付きます。
#統計 うぎゃあ！😅

回帰の式が

M₁: y = β₀ + β₁ x₁ + ε, ε ～ N(0, σ₁²)

ではなく、

【M₁: y = β₁ x₁ + ε, ε ～ N(μ₁, σ₁²)】(p.142)

【ただし、ε ～ N(μ, σ²) は誤差項εが平均μ、分散σ²の正規分布に従う、ということを示している】(p.143)

になっていた！

誤差項の平均がμ‼️😱 Image
#統計 p.17の図1.1では「Major axis」が回帰直線になっていたし、p.139では【最尤法の他に～最小二乗法】があるかのような説明の仕方になっていたし(最小二乗法は最尤法の特殊な場合)、嫌な予感はしていたのですが、pp.142-143では、

回帰の誤差項の平均がμ‼️

という設定を採用していた‼️😅😅😅 ImageImageImage
#統計 線形回帰において

y = a + bx + ε、ε〜Normal(0,σ²)

における回帰係数a,bと誤差の大きさσ²は別扱いするパラメータです。

最小二乗法(=このモデルの最尤法)でaとbはyのデータについて線形に決まる仲間のパラメータです。

この辺は学部レベルの統計学で習っている人もいると思います。
#統計 実際には上で引用したpp.142-143の前のp.141の段階で

誤差項の平均がμ‼️

という設定になっています。

「誤差項」という日本語の意味がよく分かっていないんですかね？

引用部分について他にも言いたいことがあるのですが、皆さんにまかせます。

全体的に作りが雑で杜撰という印象が確定。 Image
#統計 この本を他人に勧めている人がこの本を本当に読んだかどうかは相当に非常に疑わしい。

少なくとも、まだ統計学について十分詳しくなっていない人に、こんな雑なものを勧めちゃダメであることは確実だと思います。

「期待値」とか「線形回帰」についての常識的な解説さえ著者はできていない‼️😱
#統計

【確率変数が持つ分布を特徴付ける値を、その期待値～という】(p.31)

という説明が出版済み書籍に残っていることにも驚いたが、pp.141-143で

線形回帰の誤差項の平均はμ‼️

という設定が採用されていることにもびっくりしました。

「誤差項」という言葉の意味さえよく分かっていない感じ。
#統計 これは非常に残念なことで、どこかの段階で、雑で杜撰な説明を排除する努力をしていればこんなことにならなかった。

普通に学部教科書レベルの統計学を知っている人が丁寧にレビューしていればこんなことにはならなかったと思う。
笑った顔を見せずに、わざと「とがったこと」を言いまくる議論を楽しもうと思っていたのですが、そういう空気では無くなって来た感じ。😭
あ、【普通に学部教科書レベルの統計学を知っている人が丁寧にレビューしていればこんなことにはならなかったと思う】は、レビュワーを責めているように受け取られかねないよくない発言でした。ごめんなさい。

全責任が著者個人のみにあることは言うまでもない。
#統計 解説

データをY_1,…,Y_nの平均μと分散σ²を計算して、データを正規分布モデルNormal(μ, σ)でフィッティングすることは、単純な正規分布モデルの最尤法に一致しています。

要するに、標本の平均と分散の計算は本質的に単純な正規分布モデルの最尤法とみなせます。続く
#統計 解説続き

上の単純な正規分布モデルの最尤法は線形回帰の特別な場合

y = β₀ + ε, ε～Normal(0, σ)

であるともみなせます。ここではμではなく、β₀と書きました。

これは通常の線形回帰の場合に

y = β₀ + β₁ x + ε, ε～Normal(0, σ)

と一般化される。続く
#統計 通常の線形回帰の場合

y = β₀ + β₁ x + ε, ε～Normal(0, σ)

における β₀ + β₁ x の部分が、単純な正規分布モデルの記号における μ (の一般化)にあたるものです。そのことは尤度函数を真面目に書き下せば特に分かりやすくなると思います。
#統計 単純な正規分布モデル

y～Normal(μ, σ)

のデータY_1,…,Y_nに関する尤度函数は

L(μ, σ) = (1/√(2πσ²))ⁿ exp(-((Y_1 - μ)²+…+(Y_n - μ)²)/(2σ²))

です。y～Normal(μ, σ)は

y = μ + ε, ε～Normal(0, σ)

と書いてもよい。続く
#統計 線形回帰モデル

y=β₀+β₁x+ε
ε～Normal(μ, σ)

のデータ(x_1,Y_1),…,(x_n,Y_n)に関する尤度函数は

L(β₀,β₁,σ) = (1/√(2πσ²))ⁿ exp(-((Y_1 - (β₀+β₁x_1))²+…+(Y_n - (β₀+β₁x_n))²)/(2σ²))

です。上の単純な正規分布モデルのμ達をβ₀+β₁x_i達で置き換えた形の式になっている。
#統計 続き。すぐ上の線形回帰の場合のデータを生成している確率法則を次のように書くこともあります。

Y_i = β₀+β₁x_i+ε_i
ε_i～Normal(0, σ)
(ε_i達は独立, i=1,…,n)

よくある「確率プログラミング言語」で統計分析する場合にはこれに近い文法でコードを書けるようになっていることが多い。
#統計 続き。上と同じことを

Y_i ～ Normal(β₀+β₁x_i, σ)
(Y_i達は独立、i=1,…,n)

と書いてもよい。これがよくある最小二乗法の場合です。

最小二乗法は残差ε_i達が独立同分布な平均ゼロの正規分布に従うとするモデルの最尤法に等価です。

最尤法と別に最小二乗法があるわけではないです。
#統計 任意の函数達f_1(x),…,f_r(x)の一次結合によるフィッティングを行うための最小二乗法のモデルの記述は

Y_i = β_1 f_1(x_i) + … + β_r f_r(x_i) + ε_i
ε_i ～ Normal(0, σ)
(ε_i達は独立, i=1,…,n)

とか

Y_i ～ Normal(β_1 f_1(x_i) + … + β_r f_r(x_i), σ)
(Y_i達は独立, i=1,…,n).
#統計 以上のように、残差

ε_i = Y_i - (β_1 f_1(x_i) + … + β_r f_r(x_i))

達が平均0の独立同分布な正規分布に従うとするのが、最尤法が最小二乗法と等価になるモデルの記述になります。

続く
#統計 こういう感じに、

Y_i～Normal(μ, σ)
↓
Y_i～Normal(β₀+β₁x_i, σ)
↓
Y_i～Normal(β_1 f_1(x_i) + … + β_r f_r(x_i), σ)

と統計学入門で必ず習う単純な正規分布モデルから一般の最小二乗法まで「地続きに」理解することが基本になります。

こういう地道な勉強が楽しい。
#統計 今だと、以上で書いた形の式にかなり近い表現でモデルをコンピュータに入力できて、ほぼ自動的に最尤法(上の場合には最小二乗法になる)やベイズ法の結果を表示してくれます。

そういう経験を積めば「百聞は一見に如かず！」と言いたくなる感じで理解が進み易くなると思います。
#統計 パラメータβ_j, σ達の事前分布も

Y_i～Normal(β_1 f_1(x_i) + … + β_r f_r(x_i), σ)
β_j～Prior_j()
σ～Prior_σ()

のように与えれば、即ベイズ法のモデルの記述になります。

より一般に所謂「グラフィカルモデル」の記述は上のような式で書かれることが多い。
#統計

サンプルの標本平均と標本分散の計算
=単純な正規分布モデルの最尤法
↓
最小二乗法
=残差が独立同分布な平均0の正規分布に従うとするモデルでの最尤法
↓
以上のベイズ版

のように、高校でも習うような標本平均と標本分散の計算は「地続き」でベイズ版の回帰に繋がっているのです。
#統計 以上で説明したモデルはどれも分析用の数学的なフィクション。

以上のようなモデルとは別に、データが未知の確率法則で生成されていると想定することが基本になります。

データを生成している法則は不明のままで、データのみからどこまでその不明の法則に迫れるかが基本問題になります。
#統計 最重要ポイントなので繰り返します。

①データを生成している未知の確率法則の存在を想定する。

②データの数値だけから、その未知の法則についてどれだけのことを知ることができるか、が基本問題。

③データの数値情報を使って未知の法則に迫るために、分析用の数学的モデルを設定する。
#統計 上の考え方は非常に普遍的で、仮説検定、最尤法、ベイズ統計などをその考え方で統一的に理解することが可能です。

仮説検定、最尤法、ベイズ統計は前提とする思想が違う全然別のものである、というような思い込みを心に植え付けられてしまうと、ダメになってしまうので要注意です。
#統計 これは良い質問！

#統計 そうです。「モデル内の確率法則」と誤解を招かずに済む説明の仕方をするべきでした。ごめんなさい。文字数制限の圧力に負けた。

「実際にデータを生成していると想定している確率法則」と「分析用のモデル内でのデータ生成の確率法則」は別のものです。
#統計 次の2つを同時並行的に考えることが基本になります。

①現実におけるデータを生成している確率法則(存在すると想定するが、その法則は原則として永久に未知であると考える)

②分析用のモデル内仮想世界におけるデータ生成の確率法則(実践的にはモデルをコンピュータに入力して利用する)
#統計

①現実におけるデータを生成している確率法則

②分析用のモデル内仮想世界におけるデータ生成の確率法則

は完全に別ものだと考えた上で、この2つでデータの数値は共通のものとすることによって、それらを数学的に関係付けるわけですが。その数学的な関係が統計分析の基礎付けになります。
#統計 お勧めの勉強の仕方

①の「現実におけるデータを生成している未知の確率法則」を「データがコンピュータの擬似乱数を使って生成されている場合」に置き換えて、②のモデルを使った分析でどこまで分かるかをモンテカルロシミュレーションで確認すると、理解が捗ります。
#統計 ①の「現実におけるデータを生成している未知の確率法則」は単に未知のままというより「闇の中」という感じで、統計分析の結果その未知の法則にどこまで迫れたかさえよく分からないことが多い。

そういう場合のみを見ても理解に必要な数学的法則を確認できません。続く
#統計 ①の「現実におけるデータを生成している未知の確率法則」を「自分で決めたコンピュータで実行可能なデータ生成の確率法則」にデータを繰り返し生成して、②の分析用のモデルにぶち込んだ結果を見れば、2つを比較可能になります。

そこで見える普遍的なパターンが統計分析の基礎になる。
#統計 このスレッドのずっと上の方では、私自身が

自分で決めた確率法則に従ってコンピュータにデータの数値をランダムに生成させる
↓
それを分析用のモデルにぶち込んで計算
↓
視覚化

を #Julia言語 によるソースコードを全公開してやって見せています。普遍的パターンについても解説した。
#統計

sin(x) + 正規分布乱数 でデータを生成
↓
5次式によるフィッティングの最小二乗法のモデルにぶち込む
↓
線形代数で解かずに尤度が大きくなるパラメータ値を探索する方法で計算
↓
視覚化
↓
オーバーフィッティングの様子が見える
↓
実はこれはオーバーフィッティングの普遍的なパターン
#統計

コンピュータにサイコロXを何回もふらせてデータを生成。
動画中の赤のドットが出た目の割合。
サイコロXは3の目の出る確率だけがちょっとだけ高い。
↓
「サイコロは等確率で、1,2が出易いサイコロA、3,4が出易いB、4,5が出易いCのどれか」というベイズ法のモデルにぶち込む
↓
計算して視覚化
#統計

コンピュータでガンマ分布に従う乱数でデータを生成
↓
データをモデルY_i～Normal(μ, σ)にぶち込む
↓
視覚化

データの生成確率法則はガンマ分布ですが、分析用のモデルは正規分布です。

動画の右半分は尤度函数のヒートマップ。

尤度函数のグラフを沢山見ておくことは大事なことです。
#統計

データをガンマ分布で生成
↓
モデルY_i～Laplace(a,b) (ラプラス分布モデル)にぶち込む
↓
視覚化

動画の右半分は尤度函数の視覚化。明るい部分ほど尤度が高い。

データを生成している確率法則はガンマ分布だが、分析用のモデル内でのデータ生成確率法則はラプラス分布。
#統計 上の2つの場合で、正規分布

p_{normal}(y|μ,σ) = (1/√(2πσ²))exp(-(y-μ)²/(2σ²))

とLaplace分布

p_{Laplace}(y|a,b) = (1/(2b))exp(-|y-a|/b)

の場合を特に見せたことには、ある意図がありました。続く
#統計 データ(サンプル)の標本平均と標本分散の計算は、実は正規分布モデルの最尤法でのμとσ²の推定にちょうどなっています。(最小二乗法も最尤法になっていることはこれの一般化)

標本平均と標本分散の計算という記述統計のイロハのイは実はもろに正規分布モデルの最尤法になっているのです！続く
#統計 記述統計のイロハのイには、中央値を代表値として使うことが含まれます。

実は、サンプルの中央値aとサンプルにおけるaとの差の絶対値の平均bの計算は、Laplace分布モデルの最尤法によるa,bの推定に一致！

要するに中央値を使うことはLaplace分布によるフィッティングの一部になっている。
#統計 平均よりも中央値の方が外れ値に強いことは、正規分布よりもLaplace分布の方が「裾が太い」ことに関係していると考えることができます。

記述統計のイロハのイも我々の基本的な考え方の中に自動的に取り込まれてしまう！

記述統計と推測統計を思想が違う完全に別物と思い込まない方がよい。
#統計 上の例で、データを生成する確率法則をガンマ分布にしたのは、左右非対称な分布の典型例の1つだからです。対数正規分布でもよかった。

年収の分布はガンマ分布や対数正規分布のような形で、代表値として中央値がよく使われる。その場合に近い場合をコンピュータで作ったつもりです。
#統計 年収の分布の代表値として中央値を使うことは、我々の立場では以下のリンク先のようなことをしていることになります。

無味乾燥に見える記述統計のイロハのイに過ぎない「中央値」でさえ、こんなに面白い！
#統計 以上で見せた動画を見れば、正規分布でもLaplace分布でもないガンマ分布でデータが生成されている場合に、正規分布モデルやLaplace分布モデルを適用した場合の「誤差」の程度も分かります。
#統計 もしも、データを生成した分布を含むシンプルなモデル(今の場合はガンマ分布モデル)を使用可能ならばそうした方が推定の誤差は小さくなります。

しかし、実データの分析では真の分布は闇の中です。オーバーフィッティングの心配もある。

実データの分析では分野固有の知識が決定的に重要です。
#統計 以上の計算例でベイズ法を使ったのはサイコロXの場合だけですが、他の場合もこの程度のシンプルなモデルでは最尤法ではなくベイズ統計を使ってもほぼ同じ結果が得られます。(ただし、回帰でのオーバーフィッティングはベイズ法では予測分布がぼやけるという形で観測される。)
#統計 対立を煽っていなくても、「頻度主義の統計学とベイズ主義の統計学がある」という思い込みを心に植え付けに来る文献の記述は、はなっから馬鹿にして相手をしない方が私はよいと思います。

思想について語るなら、それ以前に思想抜きに理解できる数学的事柄をしっかり勉強してからにするべき。
#統計 「予測」という言葉は「まだ観測されていない値の分布の予測」という意味で使うべきで、「すでに得られているデータを予測する」のように使うべきじゃないのですが、『統計学を哲学する』ではそういうことをやらかしています。

「哲学」を標榜しながら、数学だけではなく、言葉の扱いがずさん。 ImageImage
#統計 「予測」という言葉は統計学について語るときの最重要キーワードなので、大事に扱うべきです。

p.139に、最尤法では与えられたデータを【最もよく予測するようなモデルのパラメータを求める】と書いていますが、そこでは「予測」ではなく、「適合」「フィット」という言葉を使うべきでした。 ImageImage
#統計 p.144では、これから観測されるデータの分布の予測の意味で「予測」という言葉を使っているように読めますが、説明の仕方が十分にクリアでない。

【似たようなデータの予測】という言い方をしているせいで、その「似たようなってどういう意味？」と読者が叫ばざるを得なくなっている。 ImageImage
#統計 普通に教科書に書いてあることを知っていると、数学だけではなく、言葉の使い方がずさんな点が非常に気になり、ものすごく不快な本になっているように感じられます。

正しい考え方に興味がない人がこの本を他人に勧めている可能性があるので、みんな注意した方がよいです。
#統計 予測分布という言葉があるのだから、最尤法の場合も予測分布を定義して、その予測誤差の大きさを問題にすればよいのに、添付画像のような説明になっているせいで、おそらくほとんどの読者は理解不能になるだろう。続く Image
#統計 予測分布の平均対数尤度の一般向けの説明をしたいのだろうが、おそらく「尤度」という言葉に引きずられて、平均対数尤度を得るためにも1000人分のデータが必要であるかのような変な説明の仕方になっている。

稠密に「この著者は分かっていないな」と感じさせる説明が出て来てつらい。 Image
#統計 既知のデータY_1,…,Y_nから、次に観測されるY_{n+1}の確率分布を推測することが、典型的な「予測」です。

既知のデータY_1,…,Y_nから任意の方法で作った次に観測されるY_{n+1}の分布の予測とみなされる確率分布p*(y)が「予測分布」の一般的な定義です。予測分布の作り方は無数にある。
#統計 既知の1000人分のデータY_1,…,Y_nから、その次のY_{n+1}の確率分布を予測できればよくて、その次も1000人分である必要はない。

(Y_{n+1}, Y_{n+2}, … がi.i.d.で大数の法則が使えることの応用はまた別の話)

こういうクリアな話がことごとく奇妙なスタイルで説明されている。
#統計 データが分布q(y)のi.i.d.で生成されているときには、次に観測されるY_{n+1}の真の分布もq(y)になります。

予測分布p*(y)によるY_{n+1}の真の分布のシミュレーションの誤差はSanovの定理より、Kullback-Leibler情報量D(q||p*)の大きさで測られます。

genkuroki.github.io/documents/2016…
#統計 KL情報量で測られる誤差の大きさは、

(汎化誤差)=-(log p*(Y_{n+1}) の Y_{n+1} に関する平均)

からある定数を引いたものに等しいので、汎化誤差を小さくできれば、予測分布の誤差も小さくできる。

上のlog p*(Y_{n+1})は予測分布の対数尤度です。続く
#統計 汎化誤差の定義には、次に観測される確率変数 Y_{n+1} の1個だけあればよい。1000人分はいりません(笑)。

しかし、確率変数Y_{n+1}に関する-log p*(Y_{n+1})の平均(期待値)の計算には、未知であるY_{n+1}の真の分布が必要なので、汎化誤差そのものを我々は計算できません。
#統計 しかし、もしも既知のデータY_1,…,Y_nの数値のみを使って、予測分布p*(y)のY_{n+1}の真の分布に対する汎化誤差の代わりに実用的に使える量を計算できるならば、それを使って予測分布の誤差を下げることが可能になるかもしれない。続く
#統計 それをある条件のもとで最尤法を使った場合に可能にしたのが、赤池弘次さんです。

AICと書かれ、赤池さん自身は【an information criterion の略記】だと言っている(笑)。

赤池さんが書いたものはこういう点でも面白いのでおすすめ。

jstage.jst.go.jp/article/butsur… Image
#統計 AICを赤池さん以外の人達はより権威的は響きを持つ「赤池情報量規準」と呼ぶ傾向があります。

そういう権威的響きの印象に負けて、権威あるものだと感じたままで終わると、知性が劣化してしまうので要注意です。

「恐れ」を無くすには自分で計算してみるしかありません。

百聞は一見に如かず
#統計 ベルヌーイ分布モデルという最もシンプルなモデルの場合に、最尤法の平均汎化誤差EE[GE_MLE]や平均AIC EE[AIC]などを、サンプルサイズnごとに計算して比較するために作ったのが添付画像のグラフです。

nbviewer.jupyter.org/gist/genkuroki… Image
#統計 他にも、ベイズ統計の場合の平均汎化誤差E[GE_Bayes]と平均WAICと平均1個抜き出し交差検証E[LOOCV]も計算しています。

n→∞で全部一致することが知られているのですが、nが小さな場合にはAICの値のみが他と大きく違っていることがわかります。n=100で全部ほぼ一致。

nbviewer.jupyter.org/gist/genkuroki… Image
#統計 こんな感じで、最尤法もベイズ統計も差別せずに、適切な規準を作って比較すると、シンプルなモデルで十分にサンプルサイズを大きくすれば、結果は全部一致することが多いです。

上の場合には小さなnで最尤法のAICのみがちょっと離れており、ベイズ版のWAICの方がちょっと優れているっぽい。
#統計 こういう計算を積み重ねたことがある人ならば、たとえ対立を煽っていなくても「頻度主義とベイズ主義の異なる統計学がある」という主張の薄っぺらさがよく分かると思う。

ほんと、馬鹿じゃないかと思います。
#統計 そういうお馬鹿さん達が恥ずかしい思いをするようには十分になっていない理由についても、別口の件(算数教育問題)での経験から幾つか思っていることがあります。

こういうところにも我々の社会は改善の余地が残っているということなのでしょう。
#統計 サンプルを動かす平均ではなく、個々のサンプルごとに、真の予測誤差とAICで測ったその対応物の同時プロットが添付画像の上半分です(下半分はそのベイズ版)。

* 青線のサンプルから作った予測分布の真の予測誤差

と

* AICでのその対応物(AICの差)の破線

を比較！

nbviewer.jupyter.org/gist/genkuroki… Image
#統計

* 青線のサンプルから作った予測分布の真の予測誤差

と

* AICでのその対応物(AICの差)の破線

が見事に逆相関‼️(相関係数がほぼ-1‼️)。

AIC側の破線が0未満になるとモデル選択に失敗します。

横軸のスケールは確率に比例するように頑張ってちょうせつしてあります。 Image
#統計 AICが予測誤差の小さな予測分布を選択するための情報量規準であるという予備知識だけがあって、AICの「真の顔」を見たことがない人達は、AICと真の予測誤差のきれいな逆相関に驚くと思います。

そのように思って欲しいのでグラフを紹介しています(笑)

百聞は一見に如かず！ Image
#統計 逆相関はベイズ版でもまったく同様です。

真の予測誤差とAICのサンプルを動かす平均はnが大きいときに一致するのですが、

揺らぎの方向は正反対

になることが証明されています。(渡辺澄夫『ベイズ統計の理論と方法』p.80下から10行目) Image
#統計 グラフの横軸のスケールは確率に比例し、AIC側の橙の破線が0未満になることとAICによるモデル選択の失敗は同値なので、モデル選択に失敗する確率は低いが、失敗確率は16%と仮説検定で要求されることが多い値の5%よりはかなり大きいです。 Image
#統計 実はAIC側のグラフにあと

1.84=quantile(Chisq(1), 0.95) - 2

だけ上に持ち上げれば、0未満になる確率がちょうど5%程度になります。(対数尤度比検定に一致する！)

こういう感じでこのグラフから、AICによるモデル選択と仮説検定の関係も読み取れます。 Image
#統計 AICを使うモデル選択は、モデル達を対等に扱ってどれがもっともらしいかを判定する行為です。

それに対して、仮説検定は、帰無仮説のモデル側が選ばれ易くなるように下駄を履かせた場合(上での1.84の持ち上げが下駄を履かせることに相当)の「モデル選択」に相当しているわけです。
#統計 そして、添付画像の下半分のベイズ版のグラフが上半分の最尤法版のグラフとほぼ同じであることから、ベイズ版のWAICやLOOCVを1.84上に持ち上げてやれば、有意水準5%仮説検定をベイズ統計を経由して行うこともできることが分かります。 Image
#統計 以上のような話は、「仮説検定とモデル選択は全然違う」とか「仮説検定とベイズ統計は全然違う」とか、場合によっては「根拠となる主義・思想自体が違う」というような思い込みの毒を飲まされた人達にとって、良い解毒剤になり得ると思います。
#統計 グラフの解説を追加

どういう計算をやっているか

成功確率w=0.4の独立試行をn=100回行ったときに成功した回数kが横軸。データ「n回中k回成功」はこのようにして生成されているという設定。

横軸のスケールは成功確率w=0.4のときにn=100回中k回成功する確率に比例。

nbviewer.jupyter.org/gist/genkuroki… Image
#統計 続き

成功確率0.4でn=100回試すと、k=40回成功する確率が最も高くなる。だから、グラフ中の横軸の目盛の刻み幅(確率に比例)はk=40の周辺で広くなっており、k=40から離れるほど狭くなっている。

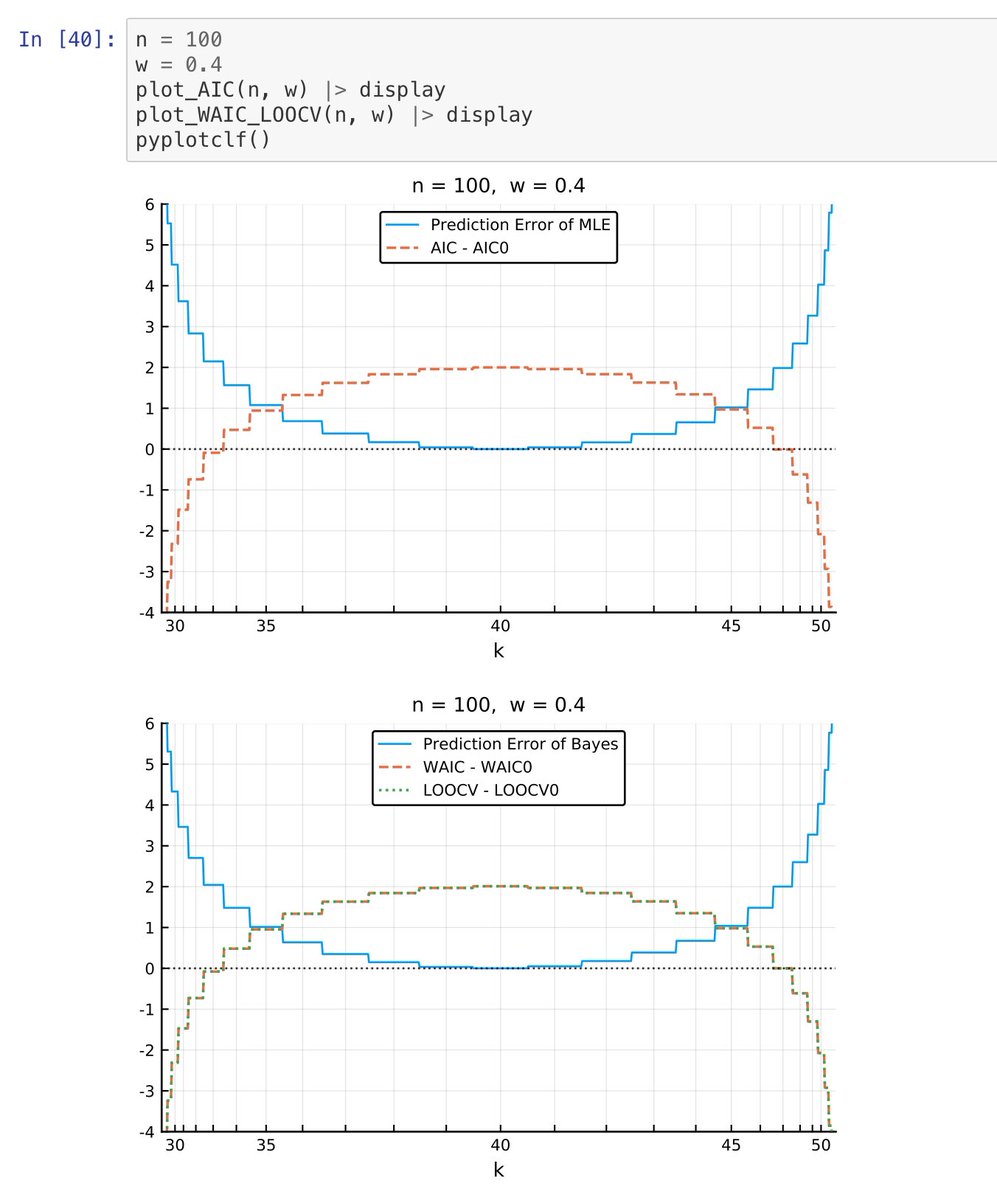
#Julia言語 のプロットライブラリにそのような機能はデフォルトでないので自分で実装した！ Image
#統計 上段のグラフは、「n回中k回成功」というデータにベルヌイ分布模型の最尤法を適用した場合。

「最尤法」と書くと難しく見えてしまうかもしれないが、実際の計算では「n回中k回成功した」というデータから「成功確率はw=k/nである」と推定するだけです。最も単純な点推定です。 Image
#統計 以下、真の成功確率をw₀=0.4と書き、データから推定した成功確率をw*=k/nと書くことにします。

このとき、真の分布は「確率w₀=0.4で成功する」で、データから最尤法で作った予測分布は「確率w*=k/nで成功する」です。そして、その予測分布の予測誤差をKL情報量で定義してやります。続く Image
#統計 予測誤差を意味するKL情報量の式は

KL = w₀ log(w₀/w*) + (1-w₀)log((1-w₀)/(1-w*))

です。上段のグラフの青線のPrediction Error of MLEはこのKLの値のグラフです。KLの値は w* = w₀ の予測分布と真の分布が一致するときに最小値の0になり、そこから離れると大きくなる。 Image
#統計 上段の橙の破線は、ベルヌイ分布モデル(パラメータは1個)の最尤法に関するAIC(以下単にAICと書く)から、モデルとして真の分布(成功確率w₀=0.4)のAICにあたるもの(AIC₀)を引いた値のプロットです。

モデル選択ではAICが小さい方が選択されます。続く Image
#統計 続き。だから、AIC < AIC₀ すなわち橙の破線の AIC - AIC₀ が負のとき、真の分布そのものではない、ベルヌイ分布モデルの側が選択され、正しいモデル選択に失敗してしまうことになります。

この場合にはAICでのモデル選択に失敗する確率は18%程度です。(上で16%としたのは誤り) Image
#統計 注意：実際にプロットしているのは、通常のKL情報量のスケールではなく、対数尤度比のχ²検定で使用されているスケールです。縦軸のスケールは自由度1のχ²分布のスケールとして意味を持っています。 Image
#統計 成功確率w₀=0.4の真の分布と、成功確率w*=k/100の最尤法による予測分布の比較では、データでの100回中の成功回数が40から離れるに従って、真の分布よりも最尤法による予測分布の方がもっともらしく見えて来るのは当然で、その当然の感覚を橙の破線のAIC - AIC₀は適切に数値化している感じ。 Image
#統計 正しいモデル選択をしたい人にとっては、AIC - AIC₀ が真の予測誤差と逆相関していることは不都合なのですが、データが運悪く偏っている場合とそうなる確率が高くてそうなった場合はデータを見他だけでは判別できないので、これは仕方がないことだと思います。 Image
#統計 AICなどの道具を使っても、運悪く低確率で生じる偏ったデータのせいで正しい分析に失敗することは防げません。

統計学を他人に勧めることはギャンブルを勧めることなので、このようにどのようなときに賭けに負ける可能性があるかについて正直に説明しないと倫理的に問題があると思う。 Image
#統計 以上のように実際にAICをプロットして、AICを使ったモデル選択について説明して、「勝率は悪くないが、運悪くデータが偏っていると賭けに負ける」という話まで説明すれば、私が「各分野固有の専門知識は非常に重要である」と言わざるを得なくなることは必然であることも理解できると思う。
#統計 AIC - AIC₀ の最大値が2になっているの理由は、パラメータが1個の場合のAICの定義によってパラメータの個数の2倍の2が足されているから。

AICとAIC₀の定義についてはソースコードを参照↓
nbviewer.jupyter.org/gist/genkuroki… Image
#統計 この手の統計学の知識は、

ギャンブルに勝つために役に立つ道具であること

や

どのような場合にギャンブルに負けることになるか

を十分に理解していてかつ、

応用先の分野についての強力な専門知識を持っている人

が使った場合に特に力を発揮するように思えます。
#統計 【重要】AICについて「モデルを複雑にすることによってモデルのデータへの適合度を上げても予測精度は下がる場合がある」というような話をするだけでは、AICと真の予測誤差がきれいに逆相関しているという重要な事実を無視してしまうので個人的に良くないと思う。具体的な計算例が大事。【重要】
#統計 『統計学を哲学する』のp.147から「AICの哲学的含意」を説明している部分を引用。説明が杜撰なのでコメントしておきます。

①【真実を「歪めた」ないし省略したモデルの方】という言い方を躊躇することなく言うのはやめた方が良いです。

なぜならば～続く Image
#統計 続き。なぜならば、現実の統計分析では、データを生成している真の法則は闇の中でずっと不明のままになるからです。

AICで選択されたモデルが、真の法則をよい近似を含んでいるから選ばれたのか、それともパラメータ数を抑えたお陰で過剰適合を免れたから選ばれたのかは闇の中。 Image
#統計 ②あと、パラメータの少ない簡素なモデルの方が【良い予測を行う場合がある】の前に【長期的には】という但し書きが付いている理由も不明。

もしかして無限の未来までデータを取得し続けて大数の法則を使うことを想定している？もしもそうならひどい誤解。 Image
#統計 パラメータが少ない簡素化されたモデルはノイズを学習してしまうリスクが小さくなる分だけ、予測性能が上がる可能性があります。

しかし、簡素化したせいで、そのモデルで実現できる真の分布の最良の近似の誤差が大きくなってしまうリスクは増える。

その両方に配慮しているのがAICです。
#統計 もう一度強調しておきますが、データを生成している真の法則は現実の統計分析では闇の中。ずっとわからないままになる。

その未知の法則に扱い易い条件(例えばi.i.d.とか)を想定した数学的に一般的な議論でAICの有用性がわかる仕組みになっています。
#統計 AICの導出で想定されている条件をデータを生成している未知の法則が小さな誤差で満たしていれば、長期的であるか否かと無関係に、AICを使ったモデル選択のギャンブルに勝つ可能性は結構高いです。

どうして【長期的には】という但し書きが付いているのか不明過ぎ。
#統計 パラメータを増やしたモデルの最尤法の数値実験を繰り返したことがある人なら、パラメータを増やすとパラメータの値が暴れ易くなって「大変なこと」になり易いことをよく知っているはずです。

それを知っていれば【パラドキシカル】(pp.146-147にある言葉)に思うこと自体がおかしい。
#統計 ③この本のp.144以降にある「平均対数尤度」は「平均汎化誤差の-1倍」を意味しているようだ。汎化誤差は、予測分布の密度函数の対数の真の分布に関する平均の-1倍。さらに予測分布は真の分布のサンプルに依存して決まるので、真のサンプル分布についての汎化誤差の平均を考えることができる。
#統計 ②追加。【長期的に】安定な法則について【長期的に】予測を出して確認し続ければ、【長期的に】安定な法則に関する新たなデータがたまりまくることになる。新たなデータも利用した方がお得(笑)。

どうして【長期的には】と但し書きを付けたのか？
#統計 ④p.149以降にある【AICは真なる分布からの距離を測るものである】という単純に間違っている主張(正しいのは実践的には計算不可能なKL情報量が真の分布とモデルで作った分布の距離を表す)についての【リアル・パターン】論は単なるたわごとだと思いました。
#統計 p.144-145の毎年1000人のデータを集める話も奇妙だったが(添付画像1)、その奇妙な話を図にしたと思われるものがp.150にあった(添付画像2)。

どうも【長期的には】という但し書きは本当にそう思っていて書かれた可能性が高い。 ImageImage
#統計 普通の考え方を再度復習。

データY_1,Y_2,…は未知の分布q(y)のi.i.d.として生成されていると想定する。

やりたいことは、データY_1,…,Y_nが既知になったときに、そのデータから次のY_{n+1}の確率分布を推測することである。

この基本設定が分かっていれば奇妙な説明にはならないはず。続く
#統計 正則性その他の条件を満たす統計モデルp(y|θ)を使った最尤法では、尤度函数 L(θ)=p(Y_1|θ)…p(Y_n|θ)を最大化するパラメータθ*を求めて、p*(y)=p(y|θ*)をその次のY_{n+1}の分布の推測結果だとする。p*(y)=p(y|θ*)は予測分布と呼ばれる。続く
#統計 上の設定ではY_{n+1}の真の分布は未知のq(y)である。

予測分布による真の分布のシミュレーションの誤差はSanovの定理より、KL情報量

D(q||p*) = ∫q(y)log(q(y)/p*(y))dy

で測られる。これは汎化誤差

G(q||p*) = -∫q(y)log p*(y) dy

と定数差しかないので、～続く
#統計 続き～、汎化誤差を最小化すれば予測分布の真の分布に対する誤差も最小化される。

しかし、汎化誤差は未知の真の分布q(y)を使って定義されているので、実践的には計算不可能。

だから、データY_1,…,Y_nのみを使って計算できる代替物を見つけたい。続く
#統計 その代替物として有名なのがAICである。しかし、ずっと上の方のベルヌーイ分布モデルの場合のように、nを大きくすると、AICと汎化誤差は逆相関するので、AICは汎化誤差の推定値としても平均汎化誤差の推定値としても一致性を持たない。続く
#統計 しかし、上の方で紹介した例では、AICを使うと正しいモデル選択に82%程度の確率で成功し、18%の確率でひどく予測を外しまくる結果の方を選択することになる。

AICによるモデル選択の実態はこういうものである。
#統計 Bernoulli分布モデル(これより易しい例はない‼️😊)の場合のAICについてはこのスレッドの上の方の以下のリンク先の前後を参照せよ。

そこではAICに関する真実が説明されている。
#統計 AICが間違ったモデルを選択してしまう場合が生じる理由は、運悪くサンプルが偏ってしまい、偏ったサンプルにオーバーフィットした側のモデルの方がAICが低くなってしまう場合があるから。

そうなる確率はそれなりに低いのですが、真実から大きくかけ離れた予測分布の側を選択してしまいます。
#統計 あるシンプルなケースでAICによるモデル選択が失敗する確率は十数パーセントになり、失敗したときの予測の外し方は非常に大きくなります。

我々の社会のリスクに関わる事柄を扱う場合にはマジで要注意だと思います。

他人にギャンブルを勧める人はリスクも強調しないと倫理的に問題がある。
#統計 真の予測誤差に逆相関するというAICとその仲間達の普遍的な数学的性質を知っていて、そのリスクについても正直に触れることが重要だという立場で、件の本のAICの哲学的含意の説明を読むことがどれだけ辛いことであるかを想像してみて欲しいです。
#統計 こういう感じで「売れ線の本」を酷評するようなことを私だって本当はしたくないのですが、AICなどに関する数学や数値実験の結果とソースコードを保有公開しているような人でなければ、このスレッドに書いたような警告を出すのは無理だと思う。

他に誰がいる？
#統計 実践的な統計学の応用では、真の法則がずっと不明のままであり、選択したモデルを実際に応用しまくるまで、サンプルが運悪く偏っていたせいでモデル選択にひどく失敗していたことに気付くことはないのです。

各分野固有の専門知識による防波堤を築くことは非常に重要です。
#統計 p.83に【分布族が対象を十全にモデル化】していなくても【ある弱い前提さえおけば、ベイズ流の更新プロセスは最終的に真理へと到達しうる】と書いてあるのですが、この部分は相当にまずい。

【Earman, 1992, pp.144-149】に何が書いてある？

ミスリーディングな要約をしているのでは？続く Image
#統計 極端な話として、パラメータを1つも持たない分布族=固定された確率分布で真の分布と違うものを採用すれば、ベイズ更新しての何も更新されず、真実とは異なる固定された確率分布がそのまま予測分布として固定されたままになります。続く
#統計 もしも仮に未知の分布q(y)の無限に長いi.i.d. Y_1, Y_2, Y_3, … が得られたならば、ベイズ統計とは無関係に、未知だった分布 q(y) が分かってしまいます。

しかし、これは理想化され過ぎた設定を採用しているので、推測統計学的には意味がないです。
#統計 データが未知の分布q(y)のi.i.d.として生成されているという想定で、統計モデルp(y|θ)を使った未知の分布q(y)の推測を行うときの限界は、分布族p(y|θ)内の分布でq(y)を最良近似するものになる。ベイズであろうがなかろうが同じ。

モデルで実現可能な分布の範囲内での最良の結果が限界になる。
#統計 以下のリンク先の動画はモデルの範囲内での最良の結果にベイズ更新が収束している例になっています。

しかし、モデルが真実の分布を含まないので、べいず更新の収束先は真実から程遠いものになっている。

こういう例の視覚化はこのスレッドに他にも色々あります。

こういう例が大事。
#統計 【分布族が対象を十全にモデル化】していなくても【ある弱い前提さえおけば、ベイズ流の更新プロセスは最終的に真理へと到達しうる】(p.83)という説をとなえるのは、さすがに非常識的過ぎる。

他人にこの本を紹介するときには、この手の事柄について警告しておかないと非常にまずいです。 Image
#統計 【確率変数が持つ分布を特徴付ける値を、その期待値～という】(p.31)という説明の仕方もひどい。本当にそう書いてあります！

統計学では「確率分布を特徴づけるパラメータ」という言い方が頻出なので常識があればこういう説明の仕方はできなかったはず。 ImageImage
#統計 p.17の図1.1の【「Major axis」と表示されているのが回帰直線】はひどいデタラメ。

p.139で【最尤法の他】に【最小二乗法】があるかのように書いていますが、最小二乗法による回帰は最尤法の特別な場合。

pp.142-143では

　回帰の誤差項εの平均がμ‼️

という設定を採用😭

色々非常識的過ぎ
#統計 【誤差項ε】について

【M₁: y = β₁ x₁ + ε, ε ～ N(μ₁, σ₁²)】(p.142)

【ただし、ε ～ N(μ, σ²) は誤差項εが平均μ、分散σ²の正規分布に従う、ということを示している】(p.143)

と書いてあることには

　ε→∞

と似た可笑しさがあると思う。🤣

「誤差項ε」なのに！😅 Image
#統計 回帰モデル

y = β₀ + β₁ x₁ + β₂ x₂ + ε, ε～Normal(0, σ²)

におけるεは「残差」と呼ばれます。

「残差」を気楽に「誤差」と呼んでしまうこと自体は許されても、「回帰モデルの期待値と観測値の差またはそのモデル化」と「真の値と観測値の差」を混同するのは非常にまずいです。
#統計 『統計学を哲学する』p.149でのAICに関する説明はずさん過ぎてひどいので読者は注意した方がよい。

この本を素晴らしいと言っている人達は「馬脚を現した」とみなして、その人が今後統計学がらみのことを言っていても、内容のまともさを疑うようにした方がよい。 Image
#統計 『統計学を哲学する』p.149でのAICに関する説明はずさん。

モデルで記述できる法則の中に真の法則をよりよく近似するものが含まれているかどうかと、データを用いてそのようなものを実際に見付けることができるかどうか全然違う問題。

その区別を前面に出さずに説明するのはまずい。続く Image
#統計 モデルで記述できる法則の中に真の法則をよりよく近似するものが含まれているかどうかと、そのようなものを実際に見付けることができるかどうかを区別するという当たり前の話を当たり前に聞こえるように説明するのではなく、それらを混同し易くした上でそれらの区別に関わる説明をするのは悪質。 Image
#統計 パラメータを増やしてどんどんモデルを複雑にして行けば、その中に真の法則をよりよく近似するものが含まれる可能性は増えます。

しかし、限られたデータを使った推定では、モデルの複雑化が原因のオーバーフィッティングが起こって、大外しの推定しかできなくなる危険性が増す。続く
#統計 続き。その2つのバランスを取って、予測分布の予測誤差がより小さくなる可能性が高くなるようなモデル選択を目指すための道具の1つがAICです。

「バランスを取る」という説明がバランスの取れた誤解されない説明の仕方だと思います。

『統計学を哲学する』の説明はバイアスをかけすぎ(笑)
#統計 そして何よりもまずいのは、AICを使ったモデル選択がどのように失敗するかについて説明しようとしていないことです。

ある種の場合に、AICは小さいが無視できない確率で(私が示した例では十数%)、予測誤差が非常に大きな予測分布を与えたモデルの側を選択します。

この事実は非常に重要！ Image
#統計

* AICはバランスを取っていること

および

* AICは小さいが無視できない確率で(私が示した例では十数%)、予測誤差が非常に大きな予測分布を与えたモデルの側を選択してしまうこと

を理解していれば、『統計学を哲学する』における「AICの哲学的含意」は薄っぺらなものに見えるはずです。 Image
#統計 AIC以前の問題として、「予測分布の汎化誤差」のような概念について著者は標準的な理解をできていない可能性については以下のリンク先を参照。

【長期的には】という謎の但し書きの問題。
#統計 AICは「予測分布の汎化誤差(の2n倍)」または「予測分布の汎化誤差(の2n倍)の平均値」(平均は真の標本分布に関する平均)の推定値。

「汎化誤差」が低い=予測の誤差が小さいことについて、【長期的には】と但し書きをつけているのは非常に奇妙。
#統計 以下のリンク先の話は「バイアスとヴァリアンスのトレードオフ」の話です。

"AIC" バイアス バリアンス トレードオフ をGoogleで検索↓
google.com/search?q=%22AI…

トレードオフなのでバランスを取るという発想になる。
AICはもろにそうです。
#統計 ツイッターで検索すると相当にまずい部分があることには触れずに、『統計学を哲学する』がまるでよい本であるかのように評価している人達が容易に見つかります。

まずい部分を正確に指摘訂正した上で、良い部分をひろって解説してくれるのなら良いのですが。
#統計 AICの定義は

-2log(最大尤度) + 2(パラメータの個数)

です。AICは小さい方がよく、モデルのパラメータ数の2倍のペナルティが課されいる。

簡単のため、パラメータwを持つ統計モデルp(y|w)のw=w₀の場合がデータY_1,…,Y_nを生成している真の分布だったとします。続く
#統計 モデル p(y|w) の尤度は

L(w) = p(Y_1|w)…p(Y_n|w)

で、これはw=w*で最大になるとします。一方、真実をぴったり表しているパラメータを持たないモデルq(y)=p(y|w₀)の尤度はL(w₀)になります。このとき、必ず

L(w*) ≧ L(w₀)

になります。続く
#統計 この場合には、真実を表すモデルの尤度L(w₀)よりも、最尤法で選択されるパラメータの尤度L(w*)の方が一般に高くなります。(尤度を単純に「もっともらしさ」だと思ってはいけない。)

尤度はモデルをデータにフィットさせたときに大きくなる量に過ぎず、真実が何かと無関係に大きくなる。続く
#統計 パラメータを増やすと以上のような仕組みで、モデルをデータにフィットさせることによって推定結果が真実から余計に離れてしまう可能性が増えてしまいます。

だから、モデルのデータへの適合度(=尤度)だけではなく、モデルのパラメータの個数も気にしなければいけない。
#統計 そのときに、-2log(最大尤度)にパラメータ数の2倍のペナルティ項を足したものが、予測分布の汎化誤差(もしくは平均汎化誤差)の2n倍の(一致性を満たさない)推定値として使えることを示したのが、赤池弘次さんです。これがAIC!
#統計 その議論の本質は、現在では汎化誤差と呼ばれることが多いエントロピー的な量と対数尤度の関係に気付くことでした。

赤池さんによれば、最尤法の開発者のFisherもその点に気付くことができておらず、ゆえに尤度の概念を正しく理解できていなかった。
#統計 以上では、簡単のため、パラメータwを持つ統計モデルp(y|w)のw=w₀の場合がデータY_1,…,Y_nを生成している真の分布だと仮定しましたが、「真の分布」という言葉を「帰無仮説のモデルになっている分布」に置き換えれば、そのまま仮説検定の典型的な状況に一致します。続く
#統計 続く。実際、その場合のAICは対数尤度比のχ²検定という非常に一般的な仮説検定の枠組みの中での特別な場合として理解可能です。

AICの理論の対数尤度比のχ²検定の理論に対する優位性は、全く無関係なモデルの比較を可能にすることです。
#統計 「黒木とか言う嫌な奴に絡まれるのが嫌だな」と思っている人は赤池弘次さんによる1980年の2つの論説を読んで理解しておけば心配せずに済むようになります(笑)

ismrepo.ism.ac.jp/index.php?acti…
統計的推論のパラダイムの変遷について

jstage.jst.go.jp/article/butsur…
エントロピーとモデルの尤度
#統計 赤池弘次さんが言うところのエントロピー側の話の統計学がらみの部分はKullback-Leibler情報量のSanovの定理としてまとめられます。Sanovの定理を使った統計力学と類似の議論については以下のリンク先の私のノートを参照。学部2～3年レベル。

genkuroki.github.io/documents/2016…
KL情報量とSanovの定理
#統計 おそらく、大学で統計学に講義を聴いたのに、AICの概念が分かりにくく感じられるのは、KL情報量のSanovの定理について知らないから。

KL情報量D(q||p)は「分布pに従う乱数生成でで分布qをシミュレートしたときの誤差の指標」という意味を持つことがSanovの定理の内容です。
#統計 統計学を理解するための、確率論における「三種の神器」は

* 大数の法則
* 中心極限定理
* KL情報量のSanovの定理

の3つです。前者の2つは教養として普及していますが、最後の1つは十分に普及していない。
#統計 未知の分布qが生成したデータを使って、コンピュータ内にモデルの分布pを作り、分布pに従う乱数生成で、未知の分布qをシミュレートする、というようなことをする場合には、

KL情報量D(q||p)=分布pに従う乱数生成で分布qをシミュレートしたときの誤差の指標

がもろに関係して来る。
#統計 Sanovの定理によって、

KL情報量D(q||p)=分布pに従う乱数生成で分布qをシミュレートしたときの誤差の指標

だと知っていれば、KL情報量D(q||p)がqとpについて非対称であることも「当然非対称になる」と理解できます。
#統計 統計学における予測分布の例と予測誤差の最もシンプルな例

成功確率が未知の値qのベルヌイ分布の独立試行の結果、n回中k回成功したとします。

そのデータから、未知の成功確率はp=k/nに近いだろうと推測したとします。

そのとき、成功確率p=k/nのベルヌイ分布を予測分布と呼びます。続く
#統計 モデルとして作った成功確率pのベルヌイ分布(予測分布)による予測は、「次に成功する確率はpであろう」という予測です。

「次にせいこうするだろう」とか「次に失敗するだろう」というような成功・失敗の予測ではないことに注意が必要です。

成功確率を予測していることに注意！
#統計 以上の状況における予測分布(成功確率p)による真の分布(成功確率q)のシミュレーションの誤差はKL情報量によって

KL(q, p) = q log(q/p) + (1-q) log((1-q)/(1-p))

と表されます。添付画像はqを0.4に固定した場合のこれのグラフ。p=qで最小値0になる。

wolframalpha.com/input/?i=plot%… Image
#統計 ベルヌイ分布モデルの場合のKL情報量やそれで表される予測分布による予測誤差は高校レベルの数学で十分に理解できるはずです。

こういう易しい話を積み重ねることが大事。

既出の nbviewer.jupyter.org/gist/genkuroki… ではAICも計算しまくっています。自分で計算してこれと比較すれば答え合わせができる。
関連
#統計 さて、上のベルヌイ分布モデルの場合のAICを計算してみましょう。

成功確率qが固定された真の分布の「n回中k回成功」というデータのAICは、パラメータがないので、単にその真の分布の尤度の対数の-2倍になります:

AIC₀ = -2k log q - 2(n-k)log(1-q).

続く
#統計 成功確率pのベルヌイ分布モデルにおける最大尤度の-2倍はp=k/nの場合の

-2log L = -2k log(k/n) -2(k-n) log(1-k/n)

になり、AICはこれに2を足したものになる:

AIC = -2log L + 2.

続く。
#統計 記号の簡単のため

p = k/n

とおくと、ベルヌイ分布モデルのAICと真の分布のAICの差は以下のように書けます！

AIC - AIC₀
= -2n(p log(p/q)) + (1-p)log((1-p)/(1-q)) + 2
= -2n KL(p, q) + 2

一方、ベルヌイ分布モデルの予測誤差は

KL(q, p) = q log(q/p) + (1-q) log((1-q)/(1-p)).
#統計 ベルヌイ分布モデルのAICと真の分布のAICの差は

AIC - AIC₀ = -2n KL(p, q) + 2

で、ベルヌイ分布モデルの予測分布の予測誤差の2n倍は

2n(予測誤差) = 2n KL(q, p)

なので非常に似ています。p, q の位置の交換と符号と+2の項の違いがある。続く
#統計 KL情報量は0以上で、KL(p, q)とKL(q, p)はpとqが近いときにほぼ一致しているので(添付画像)、推定成功確率p=k/nが真の成功確率qに近い部分で、「+2の項の下駄」を無視すれば、AICの差と予測誤差は上下対称の関係になっていることが分かります。 Image
#統計 q=0.4でn=100の場合のAICの差と予測誤差を同時プロットしたものが既出の添付画像の上段です(横軸は確率の大きさに比例)。それらは確かに(ほぼ)上下対称の関係になっています。

以上の話で出て来た数学は高校で習っているものばかりです！

ソースコード↓
nbviewer.jupyter.org/gist/genkuroki… Image
#統計 AICの差と予測誤差が上下対称の関係になっているという事実は、実践的な状況では未知の真の分布を使わないと求まらない真の予測誤差と、データのみから計算できるAICがきれいに逆相関していることを意味しています。

こういうことは高校数学をしっかり勉強していれば理解できます！
#統計 以上の計算は高校レベルでしたが、大学で習う数学を使えば、AICと真の予測誤差の逆相関を一般的に証明できます(渡辺澄夫著『ベイズ統計の理論と方法』の第3章)。

しかし、数学は簡単なことの積み重ねなので、以上で紹介した高校レベルの簡単な場合を理解するべきです。
#統計 既出の添付画像の下段はベイズ統計の場合です。ベルヌイ分布モデルにおいて、事前分布がおとなしめなら、「頻度主義」と「ベイズ 主義」の意味での主義によらず、数学的性質は同じになる。

性質が同じ数学を現実に適用するときに、主義が違うという理由で全然違うものとして扱うのは不合理。 Image
たとえ対立を煽っていなくても、「頻度主義とベイズ主義は違う」などと好んで言いたがる人達は、私の目には、かけ算順序問題を氷山の一角とする算数教育の問題について「算数と数学は違う」と言って来る人たちと同類に見えて仕方がない。

まずは主義の話の前に普通に数学を勉強してくれと言いたい。
#統計 大事な話なので繰り返しておきますが、添付画像のような、AICと実践的には真の値を知ることができない真の予測誤差のきれいな逆相関について知れば、普通の常識範囲の推論によってAICを使うときのリスクについても理解し易くなります。 Image
#統計 横軸のkは「n=100回中k回成功」というデータを表し、スケールは確率に比例。真の成功確率は0.4に設定してあるので、k=40の確率が最大。

AIC-AIC₀<0のとき、AICは真の分布ではなく、成功確率k/nの予測分布側を選択する誤りを犯します。

その選択に従うと予測を大外ししてしまいます！ Image
#統計 こんな感じにグラフを描けば

* AICによるモデル選択は、データが運悪く偏っている場合に脆弱で、そういう場合には大外ししている予測分布を与えるモデルの側を選択してしまう

* AICの差と(実践的場合に知ることができない)真の予測誤差は逆相関している

ということがすぐにわかる。 Image
#統計 以上は2点集合上の確率分布の場合の「予測分布の予測誤差」と「AICの差」の計算です。

それはそのまま有限集合上の場合に一般化可能です。

全く同じ計算！

任意の確率分布は有限集合上の確率分布で近似可能なので、そこまでやっておけば相当に一般の場合の様子を理解したことになります！
#統計 ℝ上の確率分布は、ℝを有限個の区間に分割して、各区間にその区間に入る確率を与えたもので近似できます。分割を細かくして行けば近似の精度が高まって行く。

有限集合上の確率の場合を詳細に計算して知っていれば、一般の場合の様子もイメージできるようになって来るはず。
#統計 「AICの〇〇的含意」について語りたければ、まずはAICについて理解してからにしないとダメ。当たり前の話。

せめて高校数学レベルで理解可能なことについて説明できないとまずい。

あと統計学の利用はギャンブルそのものなのでそのリスクについても正直に説明するべき。
#統計 KL情報量の

D(q||p) = ∫q(y) log(q(y)/p(y)) dy

とD(p||q)のp=qの近くでの比較は

p=q+h, ∫h(y)dy=0

とおいてhについて展開すれば分かります。

q log(q/(q+h)) = -h + h²/q - h³/(3q²) + …
(q+h)log((q+h)/q) = h + h²/q - h³/(6q²) + …
hの1次の項は積分すると消え、2次の項は一致。
#統計 そう言えば、「尤度原理」の話(がくだらないこと)について、再度説明するのを忘れていましたね。尤度の概念について40年以上前から分かっていたことについては、赤池弘次さんの1980年の論説での解説がベストだと思います。

「尤度原理」について語りたい人は尤度の概念を理解する必要あり！続く
#統計 赤池弘次さんの1980年の2つの論説はこれ↓

ismrepo.ism.ac.jp/index.php?acti…
統計的推論のパラダイムの変遷について

jstage.jst.go.jp/article/butsur…
エントロピーとモデルの尤度

数え切れないくらい繰り返し、みんなに勧めて来た。

以下ではこれらを読んでいることを前提とします。続く
#統計 尤度は「もっともらしさ」の指標ではありません。

サンプルサイズnを無限大に飛ばしたときにのみ、尤度(の対数の1/n倍)は「もっともらしさ」の正しい指標の1つである汎化誤差に一致する。

尤度を見て「もっともらしさ」を測ろうとすることは、n→∞を前提としてしまっていることになります。
#統計 「頻度主義」だとか「ベイズ主義」だとかそういう話は後回しにして(もしくはくだらない話なので永久に触れないことにして)、素直に通常のP値とベイズ 統計の事後分布におけるP値の類似物を計算して比較すると、簡単なモデルではほぼ一致することに気付きます。続く
#統計 ただし、その一致の数学的基礎は、サンプルサイズnをn→∞としたときの中心極限定理です。

定数倍の違いを無視した尤度函数のデータのみから、すべての量が決まるベイズ 統計は、本質的にn→∞での漸近論を前提にしているとも解釈できます。

続く
#統計 私による「通常のP値」と「ベイズ統計での事後分布を用いたその類似物」の同時プロットの例は以下のリンク先などで紹介しました。

以下のリンク先の例では片側検定のP値とベイズ統計での類似物が数値的によく一致していることを示しています。
#統計 「主義」の話を後回しにせずに、いきなり「主義」の話から統計学に入門してしまうと、すべてをその「主義」の色眼鏡で眺めるようになり、誰もが見ておくべき初等的な計算をやらずに終わってしまい、そのまま死ぬまで誤解し続ける危険性が出て来ます。

「主義」の話は後回しにした方が良いです。
#統計 「誰がやっても正しく計算すれば結果は同じになること」は主義と無関係に学べる。

例えば3×4=4×3などは典型的(笑)

こういう算数レベルの話は大事です。

統計学のような解析学がらみの話題の場合には、ぴったり等しくならないが、近似的には等しくなる場合にも注意を払う必要があります。
#統計 まあ、とにかく、尤度はサンプルサイズn→∞では「もっともらしさ」の真の指標になりえるが、有限のnではそうではなく、尤度を使った分析の誤差が大きくなり得ることには注意が必要だということを覚えておいた方がよいです。

有限のnでの誤差の大きさは計算しないとよく分からないことが多い。
#統計 現実に出会う有限のサンプルサイズでは「もっともらしさ」の正しい指標ではない尤度に「原理」という言葉をくっつけて崇め奉り、その後は数学的な試行錯誤をやめて尤度の概念のより深い理解を目指すことをやめてしまうような人達は、一生の間誤解し続けるに違いありません。
#統計 1980年の赤池弘次さんによる尤度概念の解説を読めば、実際に尤度の概念について一生のあいだ誤解し続けた人達が20世紀に沢山いたであろうことを想像できると思います。

ismrepo.ism.ac.jp/index.php?acti…
統計的推論のパラダイムの変遷について

jstage.jst.go.jp/article/butsur…
エントロピーとモデルの尤度
#統計 有限のサンプルサイズnでの、中心極限定理での近似の精度は分布族ごとにかなり違います。

二項分布の正規分布による近似の精度はnが小さくても相当に良い。

しかし、負の二項分布と呼ばれる分布の正規分布による近似精度は相対的にかなり低くなります。
#統計

#Julia言語 で計算して来ました。

nbviewer.jupyter.org/gist/genkuroki…

添付画像

1. n=200での二項分布の正規分布での近似。ほぼぴったり一致。

2. n=20での二項分布の正規分布近似も悪くない。

3. nが200周辺での負の二項分布の正規分布近似。

4. nが20付近だと負の二項分布の正規分布近似は悪い。 ImageImageImageImage
#統計 以上によってやっと

oku.edu.mie-u.ac.jp/~okumura/stat/…

に書いてある「止め方で仮説検定の結果が変わる」という話を扱う準備ができました。そこでは、

* コインを投げる回数を12に固定した場合(表は3回出た)

と

* 表がちょうど3回出るまでコインを投げ続けた場合(その回数は12になった)

～続く
#統計 ～の場合の片側検定のP値がそれぞれ 7.3% と 3.3% になり、大きく違うことが紹介されています。

7.3%は二項分布モデルの、3.3%は負の二項分布モデルのP値です。

添付画像はその計算を

nbviewer.jupyter.org/gist/genkuroki…

で確認した場面です。念のために2通りの方法で計算して一致を確認しています。 Image
#統計 詳しくは

oku.edu.mie-u.ac.jp/~okumura/stat/…

の解説を見て欲しいのですが、

* コインを投げる回数nを固定して表の出た回数kを観測する場合

と

* 表がちょうどk回出るまでにコインを投げた回数nを観測する場合

では、使うべき適切なモデルの確率分布族は違います。このことは高校数学レベル。
#統計 違うモデルで確率を計算したら結果が違っていても不思議でも何でもなくて、上で計算結果を見せた片側検定のP値達は異なるモデル内における確率の一種なので、それらの値が違うことはどちらかと言えば当たり前の話。

当たり前の話を「それではよくない」と言うやつはただちにダメ扱いしてよい。
#統計 よくある解説文では「尤度原理」(←出た！(笑))の話がこの次に来たりするのですが、普通にやっておくべきことは

* 他の数値例を作ってみること。

上では n=12, k=3, θ=0.5 (θは表の出る確率)の場合の「二項分布モデル」と「負の二項分布モデル」のP値が全然一致しないことを確認しました。続く
#統計 添付画像は上のn=12の場合に対応する計算をn=120,1200,12000の場合にもやってみた結果です。

2つのモデルの片側検定のP値の違いが、nを大きくするにつれて小さくなって行く様子が見えています。

nbviewer.jupyter.org/gist/genkuroki… Image
#統計 せっかくなので、各nごとにkを動かして2つのモデルの片側検定のP値を重ねてプロットしてみましょう。

nbviewer.jupyter.org/gist/genkuroki…

nが小さなときの2つのP値の食い違いは大きいが、nを大きくするとぴったり一致するようになることが分かります。 ImageImageImageImage
#統計 統計学に限らず、解析学の応用では、定義がまったく異なる2つの値や函数が、ある極限ではぴったり一致するというようなことに注意を払う必要があります。

「ぴったり等しいかどうか」ではなく、「ある状況では近似的に等しく、別の状況では近似的にも等しくない」のように考える必要がある。
#統計 さらに、以下のリンク先を見れば分かる様に、二項分布モデルの片側検定のP値とそのベイズ統計版での類似物もnが十分大きければ、近似的に等しくなります。

以上で示したnを大きくしたときの近似的は正規分布近似(中心極限定理)を経由すれば一般的に示せます。続く
#統計 要するに、nを十分大きくすれば

* 二項分布モデル
* 負の二項分布モデル
* ベルヌイ分布モデルのベイズ統計

の結果は全部近似的に等しくなり、実践的には区別する必要はなくなるのです。

「モデルが違う」「主義が違う(笑)」と無関係に、この事実は受け入れなければいけない。続く
#統計 nが小さいときのそれらの不一致も当たり前。

nが小さな場合には、データを観測した状況に合わせて妥当な数学的モデルを選んで、nが大きいときにのみ通用する議論を使わないようにすればよいだけの話です。

尤度はn→∞の場合にのみ「もっともらしさ」の正しい指標になることにも当然配慮する。
#統計 n→∞とした場合にのみ「もっともらしさ」の正しい指標になる尤度について、有限のnにおける特別な重要性を「尤度原理」のような専門用語を作って主張したり、そのような合理性に欠けたやり方を「まともなもの」だとみなして紹介することは、控えるべきだと私は思います。
#統計 私のように正直な気持ちとして「くだらない」と思ったことを「くだらない」と公言すると角が立つので、教科書を書く人は基本になることを正確に説明することを心掛ければ十分だと思います。

* 有限のnで尤度は決して「もっともらしさ」ではないこと。

* 定義が全然違う量の近似的な一致。
#統計 訂正

❌nを大きくしたときの近似的は

⭕️nを大きくしたときの近似的一致は

正規分布近似はほとんど空気を吸うごとく使えるようになっておくと便利です。コンピュータでグラフをプロットして確認した方が経験値が楽に増えます。
#統計 重要な補足

モデルを固定すればn→∞で尤度は「もっともらしさ」の正しい指標になります。

しかし、サンプルサイズnを大きくしたお陰で詳細な構造が見えて来そうだと考えて、モデルの側をパラメータの多いより複雑なものに変える、というようなことをすると、そうはなりません。
#統計 このスレッドのトップ近くの私の発言を見直すと、いかにも「とがったことを言ってやろう」という気概に満ち溢れているのですが、途中から、単に杜撰な説明を指摘したり、具体的な計算例を見せたり、その視覚化の資料を提供したりで、雰囲気が全く変わってしまっていますね。
#統計 さすがに、「確率分布を特徴づけるパラメータ」という言い方が頻出する分野について語ろうとしているのに、【確率変数が持つ分布を特徴付ける値を、その期待値～という】(p.31)と説明しちゃうのはまずい。

これ一ヶ所だけが雑なだけなら見逃しても良いが、ほとんど稠密に説明が雑でひどい。
#統計 p.83には【分布族が対象を十全にモデル化】していなくても【ある弱い前提さえおけば、ベイズ流の更新プロセスは最終的に真理へと到達しうる】と書いてある！(おそらくEarman, 1992を不適切に引用している)

もう「ベイズ主義」とか言ってもいいから、こういうのは勘弁して欲しいです。 Image
#統計 未知の分布に従う独立試行で生成された無限サイズのデータY_1, Y_2, Y_3, …が得られれば、未知の分布が未知でなくなる、という話であればベイズ統計とは無関係な話になります。

統計モデルも無関係。
#統計 ベイズ統計は数学的に難しいので色々雑になるのは仕方がないかもしれないが、

p.17の図1.1【「Major axis」と表示されているのが回帰直線】‼️

p.139に【最尤法の他】に【最小二乗法】があるかのように書いてある‼️

pp.142-143では、回帰の誤差項εの平均がμ‼️ ImageImageImage
#統計 AICで推測されるモデル間の予測の良さがどういうものかについての説明も相当におかしい。

問題：汎化誤差という用語の定義について学び、それがどのように予測の良し悪しと関係しているか説明せよ。

この問題に答えることができないうちは【AICの哲学的含意】について語るべきではなかった。
#統計 実際には、AICと予測の良し悪しの相対的な比較のための正しい指標である汎化誤差は違っていて、平均からの揺らぎは逆方向になるので、AICを使ったモデル選択によって、大外ししているひどい予測を与えるモデルの側を選択してしまうリスクもある。

こういうリスクを覆い隠す哲学談義は有害。
#統計 関連
#統計 この本のAICに関する説明を読んで感心してしまった人は次の問題に正しく回答できるだけの理解が伴っているかを確認した方がよい。

問題：自分で設定したデータの生成法則と統計モデルについてAICの簡単な計算例を挙げ、そうやって計算したAICの値と予測の良し悪しとの関係について説明せよ。
#統計 理論の詳細を理解していなくても、簡単な場合について具体的に計算例を示しつつ計算結果の解釈について他人にきちんと説明できれば、実用的には十分な理解度に達している場合が多いと思う。

1つも計算例を挙げて説明できなければ何も理解していないと判定される。
一般に本を読んだ結果を自分が理解しているかを確認するための方法として、「その本に書かれていない例を自分で作って説明できるか？」と自分に問うことは鉄板の定跡だと思います。

単なる印象を受け入れただけでは理解したことにならない。
#統計 特に渡辺澄夫著『ベイズ統計の理論と方法』の読者のために「主観確率」「ベイズ主義」「意思決定論」的なベイズ統計の解釈について以下のリンク先で解説しておきました。

何が問題なのかを正確に理解したい人は読んで下さい。

#統計

①未知の分布に関する推測や予測のみが統計学の内容である

と考えるのは__誤り__。しかし、

②未知の分布に関する推測や予測を完全に捨て去ると統計学の名に値しなくなる

と考えることは穏当。

穏当な主張である②を①だと誤解して触れ回る行為は悪質！

#統計 「主観確率」「ベイズ主義」「意思決定論」的なベイズ統計の解釈では、最初から、未知の分布に関する推測や予測を扱えないことは明らかなんですね。

そういう明らかな欠点を持つ不自由な解釈から出発するのは非常に愚かな行為だと思う。

一歩下がって別の地点から出発した方がよいです。
#統計 「主観確率」「ベイズ主義」「意思決定論」的なベイズ統計の解釈について統計学初心者に説明する場合には、「この解釈のもとでのベイズ統計では未知の分布の推測や予測は扱えないので統計学の名に値しません。そのことを十分にご了承お願いします」と但し書きを付けないとダメ。
#統計 「主観確率」「ベイズ主義」「意思決定論」における主観的な期待リスク最小化は数学的にそれなりに面白い話ではあると思うので、解説してくれる人達が継続的に現われることが望ましいです。

しかし、正直に語るべきことを語らないのは非常にまずいです。
#統計 だから、『統計学を哲学する』においても、「主観確率」の「ベイズ主義」でのベイズ統計の解釈について述べるときに、「未知の法則の推測や予測が重要なデータサイエンスには適さないベイズ統計の解釈であることに読者は注意して下さい」という但し書きが付いていれば問題なかった思っています。
#統計 実際問題として、私自身が「主観確率」「ベイズ主義」「意思決定論」の解釈に基くベイズ統計についてインターネット上に解説を公開しているくらいなので、そういう解説をする行為自体を私が非難するはずがない。
#統計 解説を書くときには、「未知の法則の推測や予測を扱わずに、主観内での期待リスクを最小化するだけ」のような重大なことはできるだけ最初に述べておくことが大事です。

明らかに重大な欠点を隠して、ずっと後でそれに触れるのはよくないと思います。最初からダメなものはダメと正直に言うべき。
#統計 既出の話題。『統計学を哲学する』では

* 確率モデル=データを生成していると想定している確率分布

* 統計モデル=確率分布族

というような用語法を採用していて、読者はこの2つを厳密に区別することを強いられます。

私ならこういう用語法を一般向け書籍では採用しません。
#統計 まだ指摘していなかったこと。

【尤度関数が実際のデータ生成プロセスと似ても似つかなかったら～】

の「尤度関数」という用語の使い方も変。

尤度関数はモデルのパラメータの関数であり、データ生成プロセスと比較できるようなものではありません。

この本は細部が稠密にずさん。 Image
#統計 非常に当たり前の話だと思うのですが、『統計学を哲学する』の読者でその「AICの哲学的含意」に感心してしまった人が、AICの計算例を1つも示すことができないならば、AICについて全く何も理解できていないくせに感心してしまったということになります。

そういうのは論外。
#統計 AICの計算例を1つ以上解説できることが、大学レベルの数学をほとんど要求せずに済むレベルの要求であることは、このスレッド中で私自身が示したベルヌーイ分布モデルの場合のAICの計算例を見れば分かります。

成功失敗の確率の取り扱いと対数の計算などができれば十分。
#統計 ベルヌーイ分布モデルの場合の「n回中k回成功」というデータから得られる予測分布のAICの計算結果は

AIC = -2(k log(k/n) + (n-k)log(1-k/n)) + 2

です。この式を見れば本当に高校レベルの数学で理解可能なことがわかるはず。
#統計 続き。未知の真の成功確率をqと書くとき、上のAICから真の分布のAICを引いた結果は、p=k/nとおくと

AIC - AIC₀ = -2n(p log(p/q) + (1-p)log((1-p)/(1-p))) + 2

で、推測したいKL情報量の2n倍は

2n KL = 2n(q log(q/p) + (1-q)log((1-q)/(1-p))

wolframalpha.com/input/?i=plot%… Image
#統計 AICを使ってモデル選択をするということは、添付画像の赤線(KL情報量の2n倍=真の予測誤差の指標で未知)を青線(本質的にAIC)で近似できていると思って、もっともらしいモデルを選ぶことになります。

それらは逆相関していることに注意！ Image
#統計 1つ前の添付画像の p を k/n で置き換えて、kを離散的に動かして、さらに横軸を確率に比例するようにスケールすると、既出の添付画像上段のグラフになります。

こういうのは全部自分で計算とプロットをやり直すと理解が進みます。

nbviewer.jupyter.org/gist/genkuroki… Image
#統計 AICの計算例を1つも示すことができないくらいAICについて本当に何も理解していないくせに、信頼性に欠けたAICの解説に付属している「AICの哲学的含意」には感心してしまうような読者は軽薄過ぎる論外な読者だと私は思います。

このスレッドにはそういう人を減らす意図があります。理解は大事。
#統計 仮に私が、「理解が大事」と唱えながら、高級な数学を知らないと絶対に理解不可能な事柄への理解を一般人にも要求しているなら、「ちょっとそれはやめて！」と私を非難して然るべきです。

しかし、私は高校で習う数学で理解可能でかつ、WolframAlphaでグラフも描けることを示しています‼️😊
#統計 本当はAICについて見事に何も理解していないくせに、信頼性に欠けた「AICの哲学的含意」には感心してしまうような人にならずに済むためには、高校で教えているような数学をきちんと理解していて、WolframAlphaのような道具を使いこなせることが、どれだけ大事かも分かって欲しいです。
#統計 少し上の方に書いた式の訂正

❌AIC - AIC₀ = -2n(p log(p/q) + (1-p)log((1-p)/(1-p))) + 2

⭕️AIC - AIC₀ = -2n(p log(p/q) + (1-p)log((1-p)/(1-q))) + 2

右側のpをqに訂正。自明な誤り。これはKL情報量の2n倍は

2n KL = 2n(q log(q/p) + (1-q)log((1-q)/(1-p))

と比較されるべき量。
#統計 1つ前のツイートに書いた公式を「2点集合上の場合」とみなしたとき、その公式は「有限集合上の場合」にそのまま一般化されます。それによってパラメータが増えた場合の例も簡単に作れる。
#統計 入門的レベルの解説でよく見る「主観確率」「ベイズ主義」の「合理的」な「意思決定論」でのベイズ統計の解釈については以下のリンク先を参照。

「主観的期待リスク最小化」によるべいず的な推定や予測の特徴付けの話。未知の法則の推測の問題は扱わない。
#統計

統計学の応用では常に未知の法則の推測は無視できない。

それなのに出発点として、未知の法則の推測を扱えない「主観確率」の「ベイズ主義」の立場から出発する。

後でそれだと困ることを示唆する。

『統計学を哲学する』が採用した方針はこれ。感心できない。

典型的なマッチポンプ。
#統計 特に「データサイエンス」とか言いたいのであれば(私は「データサイエンス」という用語を宣伝目的に使うことも軽薄だと思う)、未知の法則の推測を扱えないことが最初から明らかな出発点を捨てて、以下のリンク先の考え方を出発点に据えればよい。

watanabe-www.math.dis.titech.ac.jp/users/swatanab… Image
#統計 主観外にある未知の法則の推測を無視している「主観確率」「ベイズ主義」の枠組みから出発せずに、赤池弘次さん的な「数学で推測が当たる道を作る」といういかにも「データサイエンス」と相性が良さそうな考え方を出発点にすると、既存の主義を扱う哲学の話をできなくなるという不都合がある(笑)
#統計 既存の〇〇主義を扱う哲学の話をし難くなるという理由で、データサイエンス的には無意味な未知の法則の推測の問題を無視する枠組みから出発して、それでは足りないことを示唆しながら、その枠組みを捨て切らないスタイルで本を書いて、宣伝文で「データサイエンス」を持ち出すのはみっともない。
#統計 主に〇〇主義を扱う既存の哲学っぽい話題の側に合わせるために、複数の著名な研究者たちから「それもうダメだから」とはっきり言われているスタイルの「主観確率」の「ベイズ主義」から出発することには慎重であるべきでした。
#統計 私が本当にしたかったのはすぐ上のツイートのような「尖った話」なのですが、『統計学を哲学する』の著者は期待値の概念さえまともに説明できないようなレベルであったことが判明して、目標が「この本から受ける知的な被害を軽減すること」になってしまった。
#統計 あと、「主観確率」「ベイズ主義」のベイズ統計の解釈は「意思決定論」を経由して「主観的な(=実質的にモデル内限定での)期待リスク最小化」のスタイルで定式化され、普及しています。

そのような「統計学におけるベイズ主義」と一般的な「プラグマティズム」を併置するのはまずいです。
#統計 既存の〇〇主義の話に合わせるために出発点を選ぶのではなく、統計学が育んだ素晴らしい概念について素直にかつ地道な理解を積み重ねることによって、自分自身の新しい哲学を展開できていれば素晴らしかったと思います。

『統計学を哲学する』はそれとは正反対のことをやり通してしまった。😭
#統計 上で私がやって見せたように、高校生でも計算できる場合のAICをプロットすると、実践的には未知のままになる真の予測誤差とAICがきれいに逆相関することが一目でわかります。

実はこれは非常に一般的に証明できることです。 ImageImage
#統計 データが運悪く偏ってしまったせいで、データから作った予測分布の真の予測誤差(これは未知のままになる)が大きくなると、AICは相対的に小さくなり、予測誤差が大きくなった側のモデルが選択され易くなりというようなことが起こります。(これは本質的にオーバーフィッティングの問題)続く
#統計 続く。その効果がパラメータ数によるペナルティを超えると、AICによるモデル選択に失敗し、未知のままである真の予測誤差が非常に大きくなった側のモデルを選択してしまいます。

真の予測誤差は未知のままなので、こういうリスクがあることをユーザーは十分に認識しておく必要がある。続く
#統計 続く。こういうリスクの存在は、高校生でも計算できる場合のAICを適切にかつ地道にプロットすれば分かるわけです。

こういう地道な計算も考慮に入れて「AICの哲学的含意」について語っていれば素晴らしかった。

実際には全く逆のことをやっている。
#統計 データが運悪く偏っていると、統計的な推測は基本的にデータへのフィッティングで行われ、AICや交差検証を使っても偏ったデータに適合可能な複雑で間違っていて大外れの予測を出す側のモデルを選択することを防げないのです。

データの取得が重要なことはこのことからも分かります。
#統計 社会的なリスクについてAICを使ったモデル選択を行う場合に注意するべきことも、高校生でも計算できるAICのプロットから分かります。

AICによるモデル選択が失敗するのは、データが運悪く偏っている場合で、そのとき予測分布は大外ししたものになります。続く
#統計 続き。そういう大外ししている予測分布を現実の政策決定で利用すると、実際に予測を大外しして酷い目に遭うことを繰り返して初めてモデル選択に失敗していたことに気付く訳です。

専門家の意見をよく聞いて「プランB」も準備してリスクを下げることが重要だと私は思います。
#統計 AICに限らず、統計的な推測で何かを選択することは、常にギャンブルになります。

麻雀でどの牌を捨てるかを決めるときに確率計算や統計的推測を活かすには当然なのですが、AICなどの利用はそれに近い意味で合理的です。

しかし、どのようなリスクがあるかを承知で使わないとダメ。
#統計 このスレッドの以下のリンク先以後の部分では、尤度の概念について詳しく説明した。

ポイント：尤度はモデルを固定してデータ(サンプル)のサイズnを無限大に飛ばせば「もっともらしさ」の正しい指標になるが、有限のnではそうではない。そのようなものを「原理」に据えること自体がおかしい。
#統計 続き。以下のリンク先に続く部分では、nが大きくすれば

* 固定された回数のn回試してk回成功した場合のP値
* ちょうどk回成功するまでn回の試行が必要だった場合のP値
* n回中k回成功のベイズ統計の事後分布におけるP値の類似物

がすべて(近似的に)一致することも紹介されています。続く
#統計 続き。nが小さい場合にはそれらは一致しない。

尤度はn→∞の場合にのみ正確な結果を与える指標なので、尤度のみに依存するベイズ統計版は正確性の点では劣るとも考えられる(尤度原理は根拠のない妄言)。

残りの2つのうち実際にやったことのモデル化として正確な方を選ぶべきだろう。続く
#統計 続き。実際には「試行回数nを固定、成功はk回」でも「ちょうどk回成功するまでの試行回数はn」のどちらも不適切な場合もあるだろう。例えば「〇年〇月から〇年〇月までに予算の範囲で調査できた事例はnでそのうちk回成功」の場合には、どちらにも当てはまらない。別のモデルで計算するべき。
#統計 おそらく「尤度原理」(←くだらない話)に関係する誤解を防ぐためには、仮説検定に関する標準的な見解について知っておく必要があります。

重要なポイントは、仮説検定でP値が有意水準を下回ったときに棄却されるのは、1つの仮説ではなく、前提にしたすべての事柄のどれかであることです。続く
#統計 P値や仮説検定についての標準的な見解については

biometrics.gr.jp/news/all/ASA.p…
『統計的有意性と P 値に関する ASA 声明』

を引用すれば良いでしょう。そこでも、

【P値の計算の背後にある仮定を疑う、あるいは反対する】

ということも忘れてはいけないことが繰り返し紹介されています。 Image
#統計 例えば、「母平均は0である」という仮説について、正規分布モデルを前提とするt分布を用いて求めたP値が有意水準を下回った場合には、「母平均は0である」という仮説だけを疑うのではなく、正規分布モデルの妥当性も疑う必要があるし、無作為抽出の仮定も疑う必要があるという、当たり前の話。
#統計 「ちょうどk回成功するまでの試行回数はn」に合致している負の二項分布モデルで計算した「成功確率は0.5である」という仮説のP値が有意水準を下回った場合には、「成功確率は0.5である」という仮説を疑うだけではなく、二項分布モデルの妥当性も疑う必要がある。

これも当たり前の話でしょう。
#統計 『統計的有意性と P 値に関する ASA 声明』にある標準的な見解では、「n回中k回成功」の (n, k) という数値と「成功確率は0.5である」という仮説だけからP値の値が決まるのではなく、P値は様々な前提のもとで計算されるので、その前提のすべてを疑いにかけることが強調されているわけです。
#統計 「n回中k回成功」の (n, k) という数値の組だけを報告するだけでは、そのデータをどのように得たかが曖昧になるので、データの数値を報告するときにはそのデータをどのようにして得たかに関する詳細も含めて報告するべきであることも、当然のことでしょう。
#統計 成功確率をθと書く。「n回中k回成功」というデータの二項分布モデル(試行回数nを固定)での尤度函数は

L(θ) = binom(n, k) θᵏ (1-θ)ⁿ⁻ᵏ

で、負の二項分布モデル(ちょうどk回成功するまで試行)の尤度函数は

M(θ) = binom(n-1, k-1) θᵏ (1-θ)ⁿ⁻ᵏ

でこれらは〜続く
#統計 続き～、パラメータθによらない定数倍の違いを除いて一致するので、θについて任意の事前分布を与えたときの、ベイズ統計の事後分布は一致します。

これは元のモデル達が全然違っていることから、一瞬ギョッとするのですが、～続く
#統計 続き～、尤度函数はn→∞の場合にのみ「もっともらしさ」の正しい指標になるので、nが小さな場合に一致して欲しくない場合が一致してしまうということが起こっても仕方がないとも考えられます。

nを十分に大きくすると、どれも近似的に同じになることはすでに触れた通りです。
#統計 尤度がどのような指標であるかについては

1980年の赤池弘次さんによる尤度概念の解説が面白く読めるのでおすすめです。

ismrepo.ism.ac.jp/index.php?acti…
統計的推論のパラダイムの変遷について

jstage.jst.go.jp/article/butsur…
エントロピーとモデルの尤度
#統計 データY_1,Y_2,…が未知の分布q(y)のi.i.d.で生成されているとき、モデルの分布p(y)の対数尤度の-1/n倍

-(log p(Y_1) + … + log(Y_n))/n

は、大数の法則より、n→∞でモデルp(y)の汎化誤差

-∫q(y) log p(y) dy

に収束します。汎化誤差は「もっともらしさ」の正しい指標。
#統計 理論的なn→∞の極限操作は完璧にフィクション。

nをどれだけ大きくすれば、n→∞の理想的な状況がよく近似されるかについては、ケース・バイ・ケース。
#統計 以上のような前提のもとで、『統計学を哲学する』を見ると、添付画像にように書いてある。

「データ」という用語が例えば「n回中k回成功」の場合の (n, k) という数値の組のみの情報を表し、(n, k) という数値がどのように得られたかはデータではないということになっています。続く Image
#統計 さらに、その意味での「データ」が違っていても、尤度は同じになるかもしれず、「データ」→尤度で情報が損失するのに、【だとすれば～そのモデルについて推論しうるすべてのことは～尤度に要約されなければいけない】と書いてある。

何が【だとすれば】なのか不明。ひどくずさんな議論。 Image
#統計 サイズnのサンプルの尤度(の対数の-1/n倍)はn→∞の極限を取れば、ランダムに生成される無限サイズのサンプル Y_1, Y_2, … がモデルp(y)の無数のyにおける値の情報をひろってくれます。

しかし、有限サイズのサンプルの尤度においてはモデルp(y)内の重要な情報が大幅に失われる可能性がある。
#統計 尤度を信頼し切ることができるのは、サンプルサイズnを無限大に飛ばした場合だけなのに、どうして尤度に必要な情報が集約されると信じることができるのかが不思議。

尤度原理の信者は単に尤度の概念を正しく理解できるだけの素養がないダメな人扱いが妥当でしょう。
#統計 個人的には、真っ当な考え方をしたければ、その手の基本概念を理解してなさそうな人たちの意見をきちんと疑いの目を持って見つめなければいけないと思います。

「昔の名のある立派な人達がそう言っていた」の類のことを一切根拠にせずに、強い心を持って頑張り抜かないとダメ。
#統計 自分が「こいつはアホだ」と思っても自分の側が間違っていることもあるでしょう。

自分の側がアホである可能性を気にするなら、アホであることを指摘してもらい易いように、旗幟鮮明に自分の意見をクリアに述べた方がお得。

世の中には親切な人が沢山いて色々教えてくれます。
#統計 統計学入門の教科書に昔から伝統的に書いてあるずさんな記述を真面目に相手をする価値があるものだと認めて、一般向けに受けそうな「哲学する」本を書かれちゃうと、昔からあるずさんな考え方への強烈な応援になってしまうと思う。

そういうのはやめて欲しいと思います。
#統計 「尤度原理はクズ扱いが妥当」と断言している私がベイズ統計を大好きであることは私に過去の発言を見れば明らか。

「ベイズ主義者なら尤度原理は譲れない所でしょう」のようなことを言う人もいるかもしれませんが、「ベイズ主義者」でなくても、ベイズ統計が素晴らしいことを理解できます。
#統計 尤度の話の追加

モデルp(y|θ)がパラメータθを含んでいるときも、対数尤度函数の-1/n倍

L_n(θ) = -(log p(Y_1|θ) + … + log(Y_n|θ))/n

は、大数の法則より、n→∞で汎化誤差函数

G(θ) = -∫q(y) log p(y|θ) dy

に収束する。続く
#統計 汎化誤差函数G(θ)を最小化できれば、モデルp(y|θ)の範囲内で可能な真の分布q(y)の最良近似を作れる。

しかし、汎化誤差函数はn→∞での極限でしか分からない。

その代わりに、対数尤度函数の-1/n倍のL_n(θ)の最小化(これは尤度函数の最大化と同じ)を使うのが所謂「最尤法」です。

続く
#統計 「尤度はもっともらしさなので尤度を最大化する」のでは__ない！__

「尤度はもっともらしさではなく、モデルのデータへの適合度に過ぎないが、データのサイズn→∞の極限でなら、もっともらしさの正しい指標になる。有限のnでも尤度を最大化しちゃえ！」とするのが最尤法(ちょっと乱暴)。
#統計 最尤法は、n→∞の極限でのみ正しい「尤度」という名の指標を最大化しているだけなので、有限のサンプルサイズではオーバーフィッティングでひどい結果になることが珍しくありません。

実は、その問題を解決するための1つの道は自然にベイズ統計に繋がっているのです。続く
#統計 最尤法によるオーバーフィッティングはモデルのパラメータを多くすると容易に起こります。対処法として

対処法1. モデルのパラメータ数を減らしてみる。

対処法2. モデルのパラメータ数は減らさずに、事前分布によってパラメータが自由に動けなくする。正則化の手法を使う。

などがある。続く
#統計 「Ridge正則化」「LASSO正則化」という用語を聞いたことのある人は多いはず。それらは、それぞれ正規分布、Laplace分布の事前分布を採用した場合のMAP法(事後確率最大化法)と一致します。

事前分布は最尤法におけるオーバーフィッティングの問題を緩和するために役に立ちます。続く
#統計 大昔の仕事にJames-Stein推定という話があって、非常に単純な正規分布モデルでオーバーフィッティングが起こり易い状況を考えると、データから適切に事前分布を作ってMAP法の形式で利用すると、最尤法よりも平均二乗誤差を小さくできることを比較的容易に証明できます。続く
#統計 要するに、尤度自体が不完全な指標に過ぎないので、最尤法がオーバーフィッティングを起こし易いという欠点をもっていることは最初から明らかであり、尤度以外の何かを使ってもっとうまくやることを考えるべきで、その1つが事前分布の利用なのです。
#統計 大昔の仕事であるJames-Stein推定(以下に私による解説のリンクをはっておく)まで戻って、さらに尤度は有限のサンプルサイズでは不完全な指標に過ぎないことも理解していれば、事前分布の合理的な利用に疑義を感じる暇は最初から無くなります。
#統計 事前分布を用いるMAP法までたどりつけば、MAP法で尤度函数の情報をフルに利用していない点をうまく修正すれば、通常のベイズ統計の枠組みに自然に到達してしまいます。

現在のデータサイエンスで使われている標準的な考え方は以上のようなものだと思います。
#統計 事前分布に関するまともな解説を読みたければ、Ridge正則化やLASSO正則化が事前分布を使ったMAP法の特殊な場合とみなせることについても、きちんと触れているものを読むべきでしょう。

「事前分布は事前の主観的確信の度合いを表す」という考え方を主に書いている人は勉強不足なダメな人達。
#統計 統計学のユーザーは自分の仕事の勝ち目を増やすために統計学を使っています。

「主観確率」の「ベイズ主義」で解釈されたベイズ統計では、主観の表現であるモデル内における期待リスクを最小化するだけで、主観の外側で自分のモデルがどのように勝ち目を増やしてくれるかについて一切扱わない。
#統計 だから、自分の仕事の勝ち目を増やすために統計学を使っている人は、よっぽどのバカでもない限り、「主観確率」の「ベイズ主義」のベイズ統計を使うはずがないのです。

こういう明らかなことを無視して本を書くと、『統計学を哲学する』のような本になるわけです。
#統計 対処法①のパラメータ数を減らすでも、対処法②の正則化の方法(事前分布を使うMAP法)にしても、

* モデルにバイアスがかかることによる害
* オーバーフィッティングによる害

の間でバランスを取ることになります。両方同時には改善できない。これが所謂「バイアス・バリアンス・トレードオフ」
#統計 大体においてこの手の話は「トレードオフ」の話になりがちだと思います。

「トレードオフのバランスを取る」という説明とは別の説明の仕方がされていたら、一度は疑ってみた方がよいかも。
#統計 添付画像は『統計学を哲学する』でも触れている

stat.columbia.edu/~gelman/resear…

より。ほぼ私と同じようなことを言っています。

添付画像の部分をきちんと引用して最初から「ベイズ主義」に拘らない方針にすれば、偽物ではないデータサイエンスの話をできていた可能性がある。 Image
#統計 また別の尤度の話

【データ】を重視するの立場では、【そのモデルについて推論しうるすべてのことは～尤度に要約されなければいけない】という考え方がどんなに馬鹿げているかについて。

同一の統計モデルにおいて、異なるデータに同一の尤度函数が対応する場合を簡単に挙げられます。続く Image
#統計 例えば、正規分布モデルの尤度函数は、サイズnのサンプルの平均と分散だけで決まります。正規分布モデルではデータを尤度函数で要約した途端に、データが持っていた平均と分散以外の情報は消えて無くなる。

データ重視の立場では、モデルの尤度函数ですべてが要約されるとは決してならない。
#統計 統計モデルを尤度函数の形式でのみ使う手法には、最尤法、MAP法、ベイズ法がありますが、それらの手法内ではデータの持っていた豊富な情報を尤度函数に要約する形式で分析を行なっていることにはなりますが、統計モデルを尤度函数以外の形で使ってはいけないなんて話はどこからも出て来ません。
#統計 繰り返し強調しているように、尤度はそんなに立派な指標ではなく、オーバーフィッティングの元凶になる不完全な指標にすぎません。

そういう不完全なものに「原理」という言葉をくっつけて、特権的な重要性があるかのように見せた人達は、人類社会に負の貢献をしていたと言ってよいでしょう。
#統計 データY_1,…,Y_nに関するモデルp(y|θ)の尤度函数は

L(θ) = p(Y_1|θ)…p(Y_n|θ)

で、モデルp(y|θ)のy=Y_1,…,Y_nにおける値しか反映されていない。だから、統計モデルの要約としても尤度函数はひどく不完全なものであることは明らか。

こういう当たり前の考え方を平気で蔑ろにする奴等がいる
#統計 仮説検定では統計モデルを「そのモデル内で生じる数値がデータ以上に偏る確率」の形で使うので、「そのモデル内でデータと同じ数値が生じる確率(密度)」=「尤度」以外の情報も使っています。

「尤度以外の情報を使うな」というような相手をする価値がない考え方をまとも扱いしちゃダメ。
#統計 数学のような難しい道具を使う分野が新たにできあがる過程で、開拓者たちが(数学が難しいことが原因で)不適切な考え方も同時に広めてしまうことはいくらでもあり得ると思います。

開拓者達への尊敬心を失わないままで、不適切な考え方をきちんと否定して後世に伝えるのは大事なこと。
#統計 たまに、よく分かってなさそうな人が「哲学を使えば、科学者が思いもよらないことを前提にしていたことが明らかになる」のようなことを言っているのを見ることがあるのですが、そういう人は「思い上がった勘違い君の哲学ファン」に過ぎないです。

よくもまあそういうことを言えるものだ。
#統計 科学は専門外の人が玄人に対してそう簡単に何か言えるような世界ではないです。

言えるようになるためには、専門家にも一目置かれる程度の素養を身に付けるしかないです。

例えば、回帰直線とmajor axisを混同したり、期待値についてまともな説明をできない人には無理な世界があります。
#統計 『統計学を哲学する』の問題はむしろ著者の側が余計な思い込みを入れまくって、思い込み抜きに語れる手堅い知識(特に数学を使って得られる知識)を逃してしまっているという問題があります。

そこは謙虚に「自分は何もわかっていなかった」と言った方がよいと思います。
#統計

①ベイズ統計に「主観確率」「ベイズ主義」「内在主義」などの余計なものをくっつける。
↓
②後でそれでは困ると言い出す。
↓
③今度はベイズ統計に「外材主義」「プラグマティズム」などの余計なものをくっつける。

マッチポンプ。

⓪分布を特徴付ける値をその期待値と呼んだりする(笑) ImageImage
#統計 添付画像

1. 『統計学を哲学する』より。Major axesを回帰直線だと主張😅

2. Galton 1886 galton.org/bib/JournalIte… から、私が引用。

3. 私によるその模造品

#Julia言語 によるソースコード↓
gist.github.com/genkuroki/ff0c…

loci of {vertical, horizontal} tangential pointsがの方が回帰直線 ImageImageImage
#統計 タイポ訂正

❌外材主義→⭕️外在主義
#統計 データを尤度函数で要約してしまうと、データからどれだけの情報が失われるかについての視覚化で有名なのが

ja.wikipedia.org/wiki/%E3%82%A2…
アンスコムの例 Anscombe's quartet

モデル

y = a + bx + ε, ε～Normal(0,σ²)

の添付画像のデータに関する尤度函数は全部(ほぼ)同じになります。 Image
#統計 尤度函数が同じになればベイズ統計を使っても結果は同じになります。添付画像はAnscombe's quartetのベイズ回帰の予測分布のヒートマップによるプロットです(#Julia言語 のTuring.jlを使った)。

nbviewer.jupyter.org/gist/genkuroki… Image
#統計 統計学入門において強調されている大事なことの一つが、データを一部の代表値で要約してしまうことの危険性の強調です。

Anscombeの例が有名なように、統計学の世界ではその強調は「空気の一部」になっているとさえ言えると思います。
#統計 例えば、薄青のドットのデータのプロットを省略して、ヒートマップのベイズ回帰の結果だけを示すと、すべて同じになるので、データを不適切なモデルで回帰したことがわからなくなってしまいます。 Image
#統計 添付動画は

autodesk.com/research/publi…
Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing

より。この記事では同じ要約統計量を持つ異なるデータを作る方法が解説されています。
#統計 添付動画は

autodesk.com/research/publi…
Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing

より。

box-plot (箱ひげ図)にすると区別がつかなくなる異なるデータを示してくれています。

箱ひげ図は怖い。
#統計 補足: リンク先の例では、平面上のサンプルの平均と分散共分散行列を同じに保っている。多変量正規分布モデルの尤度はサンプルの平均と分散共分散行列だけで決まるので、動画中のデータに対する尤度函数は全部同じになる。

データとモデルの尤度函数による要約はこういう類のものになります。
#統計 データを不適切にプロットしたり、不適切に要約すると、どれだけ大変なことになるかを、印象的に伝える「芸」は世界の統計学ファンの間では鉄板定番のネタだと思います。

「尤度函数」とか言われると難しくて分からなくなる人はまずこういう具体的な話から入ると良いと思います。
#統計 こういう具体的な話題を楽しんで来ているところに、「〇〇主義」「〇〇原理」の話にするために、最初から不適切であることが明らかな(しかし20世紀の暗黒時代には偉い人が何故か大真面目に語っていたこと)考え方から出発して、マッチポンプ型に議論を進める本が出版されて話題になってしまった。
#統計 一般に指数型分布族のモデルでは尤度函数を決めるデータの要約統計量達がシンプルになります。

正規分布モデルなら、データの平均と分散だけで尤度函数が決まる。

ガンマ分布モデルなら、データの平均と対数平均だけで尤度函数が決まる。

などなど
#統計 box plotに代わる様々なグラフの描き方については、以下のリンク先のスレッドが面白いです。
#統計 文脈がよくわかりませんが、『統計学を哲学する』のように【そのモデルについて推論しうるすべてのことは～尤度に要約されなければいけない】(笑)と説明している本に関係した文脈で、「AICの導出に尤度原理を使っている」と言う人がいたら、自信を持っておバカさん扱いしないとまずいです。 Image
#統計 【尤度原理～とは仮説やパラメータの推論に関するすべての情報は観測されたデータに対する尤度関数のなかに含まれているとする主張である】(p.123)の意味での、尤度原理はあまりにも馬鹿げた主張なので実践的でまともな統計学の話題には一切関係しないと最初から判断できないと困ると思う。
#統計 【尤度原理～とは仮説やパラメータの推論に関するすべての情報は観測されたデータに対する尤度関数のなかに含まれているとする主張である】(p.123)の意味での尤度原理がAICの導出に使われるかのようなことを言ってしまうと、普通はバカ扱いされてしまうものだと思います。
#統計 【尤度原理】=【仮説やパラメータの推論に関するすべての情報は観測されたデータに対する尤度関数のなかに含まれているとする主張】(p.123)という極端な考え方は普通なら最初から馬鹿げたものとみなされます。

馬鹿げていることが明らかな設定を採用することから議論を始めるマッチポンプ。
#統計 1つ前のツイートの意味での【尤度原理】のように、馬鹿げていることが明らかな設定を真面目に相手をする価値があるとみなした本を書いて販売することは、多くの人達のそういう極端で馬鹿げた考え方への抵抗力を下げることになります。人間は「権威」に結構弱い。

これが滅茶苦茶怖い。
#統計 購入した本に関する話題で知り合いがその本の意味での【尤度原理】について語っているのを見た人は、その本の意味での極端すぎて馬鹿げている【尤度原理】を馬鹿げているとみなせなくなる。さらにそういう経路で20世紀の統計学史について知ると、そういう傾向は固定されてしまうでしょう。
#統計 しかもそういう本が、統計学における基本概念を誤解し、不適切に解説したりしていると、その害は非常に大きくなる可能性があります。

【確率変数が持つ分布を特徴付ける値を、その期待値～という】(p.31)はひどすぎ。

「確率分布を特徴付けるパラメータ」という言い方は統計学では頻出。 ImageImage
#統計 データの分散共分散行列から計算される楕円の長軸と回帰直線が異なることは、統計学入門の段階でよく注意されることです。初心者が誤解しがちなので、解説側は警告しておきたくなるわけです。

『統計学を哲学する』p.17ではもろに楕円の長軸を回帰直線扱いしています。 Image
#統計 言葉の使い方(もしくは議論の仕方)が恐ろしく粗雑な点も気になります。

例えば、【尤度関数】と確率分布族の区別さえ曖昧に見える。もしかして馬鹿げていることが明らかな【尤度原理】を当然の前提にしているのか？いずれにせよ、ダメです。続く Image
#統計 よくあるi.i.d.の統計学の文脈では、パラメータθ(パラメータは期待値とは異なるものであることに注意！(笑))を持つ確率密度函数p(y|θ)のデータY_1,…,Y_nに関する尤度函数L(θ)の定義は

L(θ)=p(Y_1|θ)…p(Y_n|θ)

です。尤度函数はパラメータθの函数になる。続く
#統計 尤度函数は【実際のデータの生成プロセス】と比較できるものではありません。それと比較するべきものは、パラメータ付きの確率分布p(y|θ)の方です。

下の方の青下線部分では、【尤度関数】を【実際のデータの生成プロセス】と比較するべきもの扱い。これはひどい。 Image
#統計 これが一ヶ所だけなら筆が滑っただけともみなせるのですが、実際にはそうではない。

p.61【確率分布／確率種】
p.83【確率種／分布族】【確率種／尤度関数】【確率種／尤度関数】

とある。【確率分布】や【分布族】と【尤度関数】は全然違うものなので注意深く区別しないと確実に誤解します。 ImageImage
#統計 【尤度原理】のような馬鹿げた考え方を暗黙の前提にしているのかもしれませんが、未知の確率法則を推測するためのモデルとして用意した確率分布や確率分布族と、データに依存して決まる尤度や尤度函数は全然違うものです。

統計学初心者はおそらくその辺でも混乱しがちだと思う。
#統計 『統計学を哲学する』のずさんなスタイルは、統計学初心者が初心者にありがちな混乱を抱えたまま頑張って書かれた本だと推測すると色々辻褄が合うように思えます。

何が回帰直線であるかについての誤解や、期待値に関するデタラメな説明の仕方はまさにこの推測をサポートするものだと言えます。
#統計 初心者にとってこういうスタイルはありがちなのかなという印象は、回帰モデルの説明の仕方を見ても強化されます。

【y=β₁x₁+ε, ε～N(μ₁,σ₁²)】
【誤差項εが平均μ】‼️

というスタイルを採用している。悪いけどこれには結構受けました🤣　普通は、残差項εは平均0とします。 Image
#統計 以上で繰り返し紹介しているネタは氷山の一角に過ぎず、ぺーじをめくるたびに次々に「これはつらい」と思わざるを得ない記述がぽんぽん出て来ます。

議論の俎上に上げる以前の問題を抱えている。

この本を読んで褒めている人達はこの本を読んでいてつらくはなかったのでしょうか？
#統計 もしかして、出版スケジュールがタイト過ぎたということなのでしょうか？

もうちょっと慎重に訂正と推敲を重ねていれば、以上のようなことを言われずに済む本に仕上がったのでは？

馬鹿げた考え方を出発点にするマッチポンプ型スタイルを廃するには構成自体を変える必要がありそうですが。
#統計 #超算数 以下の2つは非常によく似ています。

* 算数教育の伝統に従って、かけ算には順序が決まっているとし、算数は数学と違うと言い張る。

* 前世紀の統計学の伝統に従って、ベイズ統計は主観確率のベイズ主義を採用する統計学であるとし、ベイズ統計と頻度主義は本質的に異なると言い張る。
#統計 #超算数 伝統的にずさんな考え方がされて来たという事実に思いが及ばずに、伝統的に言われて来たことに批判的になり切れず、伝統的に言われて来たずさんな考え方を自身の考え方の出発点に採用してしまうという誤謬。
#統計 ごめんなさい。リンクをはるのに失敗していた。

尤度について理解したい人が読むと楽しめる赤池弘次さんによる1980年の論説は以下で読めます。

ismrepo.ism.ac.jp/index.php?acti…
統計的推論のパラダイムの変遷について

jstage.jst.go.jp/article/butsur…
エントロピーとモデルの尤度

添付画像は後者より😅 Image
#統計 論説の読み方のヒント

Kullback-Leibler情報量入門では「より一般的なdivergenceの特別な場合」というスタイルの不鮮明な解説を読むよりも、赤池弘次さんの論説

jstage.jst.go.jp/article/butsur…
エントロピーとモデルの尤度

のp.610の右半分のスタイルで理解しておくのが良いと思います。続く
#統計　続き。そこで赤池さんは

(サイズNでの確率) = exp(N×S + o(N))

のスタイルの確率の漸近挙動を扱っており、統計力学におけるエントロピーとの類似が明瞭になっています(Sの部分)。この形の漸近挙動を数学者は「大偏差原理」と呼ぶことがある(大雑把な説明注意！)

漸近挙動の記述は大事。
#統計 もう1つの論説

ismrepo.ism.ac.jp/index.php?acti…
統計的推論のパラダイムの変遷について
赤池弘次 (1980)

の少なくとも第3～5節は(ベイズ統計外での)尤度の使い方に関する話だとみなせます。
#統計 第3節では、パラメータθを持つモデルの確率密度函数f(x|θ)の未知の分布g(x)のi.i.d.で生成されたデータX_1,…,X_nに関する対数尤度の1/n倍

L_n(θ) = (log f(X_1|θ) + … + f(X_n|θ))/n

は大数の法則より、平均対数尤度

E[log f(X|θ)] = ∫g(x) log f(x|θ) dx

に収束するという話。この～続く
#統計 ～平均対数尤度の

E[log f(X|θ)] = ∫g(x) log f(x|θ) dx

が「モデル f(x|θ) が未知の分布 g(x) をどれだけよく捉えているか」(大きい方がよい)を意味する正しい指標になっている理由が、もう1つの論説『エントロピーとモデルの尤度』(1980)で解説されているわけです。続く
#統計 尤度は、モデル f(x|θ) のデータX_1,…,X_nへのフィッティングの良さ(適合度)を意味し、モデル f(x|θ) の未知である真の分布 g(x) への適合度ではないのですが、n→∞の極限では、尤度の対数の1/n倍は「モデル f(x|θ) の未知である真の分布 g(x) への適合度」の正しい指標に収束する。
#統計 尤度の概念を正しく使うためには、1つ前のツイートで説明した数学的事実は必須の予備知識になるのですが、最尤法の開発普及者であるFisherさん自身は気付いていなかったらしいというのが赤池弘次さんの見立てなわけです。
#統計 ismrepo.ism.ac.jp/index.php?acti… におけるその次の第4節「カイ二乗検定」の節は本質的に最尤法に関する Wilks' theorem の話とみなせます。

数理統計学ではよく知られている結果なのですが、知らない人は検索して勉強しておくとよいです↓

google.com/search?q=Wilks…
#統計 Wilks' theoremは

* 最尤法における最大対数尤度と「仮説検定」の関係を与える定理

ともみなせるのですが、

* 「AIC」と「仮説検定」の関係を与える定理

ともみなせます。非常に基本的な定理であり、尤度の正しい使い方を知りたい人にとって必須の教養になります。
#統計 Wilksの定理は、

M₁: d₁次元のパラメータ空間Θ₁を持つモデルf(x|θ) (θ∈Θ₁)

と

M₀: それのパラメータ空間をd₀次元の部分空間Θ₀に制限して得られるモデル f(x|θ) (θ∈Θ₀)

の比較に関する結果です。
#統計 仮説検定の文脈では、パラメータ空間が大きなモデルM₁は「対立仮説」のモデル化とみなされ、パラメータ空間がその部分空間のモデルM₀は「帰無仮説」のモデル化とみなされる。

仮説検定は、帰無仮説のモデルM₀と対立仮説のモデルM₁のどちらを選択するかという問題の特別な場合になる。
#統計 例えば、ベルヌイ分布モデルにおいて、パラメータ空間をΘ₀={p₀} (1点空間)に制限した側が「成功確率はp₀である」という帰無仮説のモデル化になり、パラメータ空間をΘ₁=[0,1] (区間)にしたものが(両側検定の)対立仮説のモデル化になります。

他の多くの仮説検定がこのパターンにはまります。
#統計 データX_1,…,X_nに関する最大尤度は、パラメータ空間の大きな対立仮説のモデル化M₁の方が、パラメータ空間が部分空間になっている帰無仮説のモデル化M₀以上になります。

尤度最大化の計算時に探すパラメータの範囲が広い方が必ず大きくなる。当たり前の話。続く
#統計 nが大きなときに、パラメータ空間が大きな対立仮説のモデルM₁の最大対数尤度がパラメータ空間がその部分空間の帰無仮説のモデルM₀の最大対数尤度よりも、確率的にどれだけ大きくなるかを記述しているのが、Wilks' theoremです。

確率的にどれくらい大きくなるかがわかる！
#統計 単に大きくなるだけなら自明なのですが、適当な仮定のもとで、nが大きなときに、確率的にどのように大きくなるかまで分かるというのが、Wilks' theoremの非自明な結果です。

証明は対数尤度の差に大数の法則と中心極限定理を適用すれば得られます。
#統計

Wilks' theorem:

　(対立仮説のモデルM₁の最大対数尤度) - (帰無仮説のモデルM₀の最大対数尤度) ≧ 0

の2倍は、nが大きなときに、自由度が

　d₁ - d₀ = (パラメータ空間の次元の差)

のχ²分布に近似的に従う！

「自由度」と「χ²分布」が出て来た！
#統計 χ²検定と言えば「自由度」という用語の意味不明さが悪名高いのですが、個人的な意見では、χ²検定における「自由度」の概念を正しく理解するためには、Wilks' theoremの知識が必須です。

Wilks' theoremの予備知識を持たない人が「自由度の意味わからん」となるのは正しく分からなくなっている！
#統計 数学は下からの地道な積み重ねが基本なので、Wilks' theoremの予備知識がないくせに、χ²検定における「自由度」の概念についてわかったつもりになっている人はひどく勘違いしている可能性が高く、「自由度、意味わからん！」と正直に叫んでいる人の側の理解度および理解に迫る態度が優れている。
#統計 対立仮説のモデル化M₁の相対的に大きなパラメータ空間の次元をd₁と書き、帰無仮説のモデル化M₀の部分空間になっているパラメータ空間の次元をd₀と書くとき、その状況におけるχ²検定で使うχ²分布の自由度は d₁ - d₀ になります。これはどう見ても本質的にWilks' theoremそのものです。
#統計 もとの赤池さんの論説の第4節「カイ2乗検定」は全部で16行しかないのですが、以上のような予備知識が必要なので結構大変ですね。
#統計 あ、超絶重要な仮定を忘れていました！ごめんなさい。

以上は仮説検定の話なので、

(*) サンプルX_1,…,X_nは帰無仮説に含まれるあるパラメータθ₀∈Θ₀に対応するモデルの確率分布 f(x|θ₀) のi.i.d.として生成されている

と仮定していると読み直して下さい！

ごめんなさい。
#統計 以上を読めた人である程度以上コンピュータの扱いに慣れている人であれば、有限のnで数値的にどの程度Wilks' theoremによる近似がうまく行っているかを自分で確認できるはずです。

中心極限定理を数値的に確認している人は多いと思う。

同じことをWilks' theoremでもやってみるべき！
#統計 Wilks' theoremのコンピュータによる数値的確認が、中心極限定理の場合よりちょっとだけ面倒になる程度の手間でできることを示すために #Julia言語 でのサンプルコードを作って来ました。べた書きの最も素朴なやつ！

gist.github.com/genkuroki/6667…
#統計 添付画像は、サイズnのサンプルを標準正規分布 Normal() で生成して、帰無仮説のモデル化を標準正規分布(パラメータ数0)とし、対立仮説のモデル化を正規分布モデル(パラメータ数2)にした場合。

nを大きくすると、自由度2-0=2のχ²分布による近似が正確になって行く。 ImageImageImage
#統計 標準正規分布Normal(0, 1)でサンプルを生成し、帰無仮説のモデル化を分散を1に固定した正規分布モデルNormal(μ, 1)(パラメータ数1)にし、対立仮説のモデル化を正規分布モデル(パラメータ数2)にした場合。

最大尤度の比の対数の2倍の分布が、自由度2-1=1のχ²分布でよく近似されている。 ImageImage
#統計 2次元の多変量標準正規分布(平均(0,0)、分散共分散行列は単位行列)でサンプルを生成して、帰無仮説のモデル化を2次元の多変量標準正規分布モデル(パラメータ数0)とし、対立仮説のモデル化を2次元の多変量正規分布モデル(パラメータ数5)にした場合。

自由度5-0=5のχ²分布でよく近似されている。 Image
#統計 中心極限定理の数値的確認よりは少し面倒になりますが、各種プログラミング言語の確率分布のライブラリのドキュメントをよく読んでおけば、Wilks' theoremの数値的確認に本質的に難しいことはありません。

どんどん確認して、確率分布界の風景を心に刻み込んで行くと理解が捗ります。
#統計

①帰無仮説のモデル化に含まれる確率分布でサイズnのサンプル(乱数)を生成する。

②帰無仮説と対立仮説の最大尤度の対数を計算し、後者から前者を引いた値の2倍を計算して記録に残す。

③その値達のヒストグラムとχ²分布のプロットを重ねて表示。

サンプルコード↓
gist.github.com/genkuroki/6667…
#統計 帰無仮説のモデルに含まれる確率分布でデータ(サンプル)が生成されているとき、データを生成している法則のより適切なモデル化として選択したいのはパラメータ空間が相対的に小さな帰無仮説のモデル化の側であり、余計なパラメータを増やした対立仮説のモデル化の側ではありません。
#統計 しかし、データへのモデルの適合度を意味する尤度は、常にパラメータを増やした側(対立仮説のモデル化側)が大きくなります。
#統計 しかし、その大きくなり方はWilks' theoremによって近似的にわかっており、確率的にほとんど起こらないほど対立仮説側の尤度が大きくなってしまった場合には、データが帰無仮説のモデル化に含まれる分布で生成されているという想定が疑わしくなります。

仮説検定‼️
#統計 対立仮説の最大対数尤度の2倍から帰無仮説のそれを引いた値の分布が自由度dfのχ²分布でよく近似されているならば、その値がそのχ²分布で5%未満の確率でしか生じないほど大きな領域に入っていれば「有意水準5%で帰無仮説のモデルが棄却される」とできるわけです。

これが対数尤度比のχ²検定。
#統計 尤度はn→∞でモデルの真の分布への適合度の正しい指標に近付くのですが、n→∞の極限を取り切るのではなく、その途中の様子の漸近挙動を見ることによって、最尤法の応用として、非常に一般的な仮説検定を作ることができたわけです。
#統計 Wilks' theoremの応用として作られたχ²検定の内容とAICの定義

AIC = -2(最大尤度の対数) + 2(モデルのパラメータ数)

を比較すれば、「なぜか2倍されていること」も含めて、明らかに関係していることが分かります。

その話が赤池論説第5節で指摘されている「検定と推定の密接な関係」です。
#統計 統計学の通常の応用場面で我々は「どのモデルがより正しいか」が分かりません。複数のモデルを使って推定をやり直して比較することを行うのが普通。

そのときに、どのモデルの推定結果がもっともらしいかを判断することと仮説検定がほとんど同じようなことをしていることになります！
#統計 これによって、推定と検定は理論的に統一されるべきであることが示唆されるわけです。推定と検定を無理に分離するのはよろしくない。
#統計 上の方の記号より、

(対立仮説のAIC) = -2(対立仮説の最大対数尤度) + 2d₁
(帰無仮説のAIC) = -2(帰無仮説の最大対数尤度) + 2d₀

なので

(対立仮説のAIC) - (帰無仮説のAIC)
= -2(対立仮説と帰無仮説の最大対数尤度の差(0以上)) + 2(d₁-d₀)

d₁-d₀はχ²検定の自由度になるのでした。続く
#統計 AICによるモデル選択では、上の差の値が負になったときに、対立仮説のモデル化が選択されます。(モデル選択が失敗する場合！)

そうなるのは、近似的に自由度df=d₁-d₀のχ²分布に従う(対立仮説と帰無仮説の最大対数尤度の差(0以上))の2倍が、dfの2倍を超える場合である。続く
#統計 その確率は

df = 1 ⇒ 15.2%
df = 2 ⇒ 13.5%
…

で仮説検定で使われる通常の有意水準より高いです。

仮説検定ではこの確率を有意水準として先に与えており、AICによるモデル選択では複数のモデルを平等に扱うのでそうしない。 Image
#統計 AICは比較するモデルのパラメータ空間の間に包含関係がなくても使用できます。その代わり、通常の仮説検定と違って第1種に誤りの確率を通常気にせず、大きくなる場合がある。

Wilks' theoremやそれを基礎とするχ²検定はパラメータ空間に包含関係がないと使えない。

トレードオフがある。
#統計 クールに「似たような使い方をできる似たような道具だが、トレードオフがある」と考えて、自分にとって適切な道具を選べばよい。

異なる道具の間の思想の違いを強調して別物であるという思い込みを次世代の人たちに吹き込むことは有害。
#統計 私のツイログを「お墨付き」で検索すると、口癖のように「統計学はお墨付きを得るための道具ではない」と言っている。
twilog.org/genkuroki/sear…

しかし、『統計学を哲学する』の著者によれば、統計学は【「お墨付き」を与える主要な方法論】(p.7)らしい。

教育的に極めて有害に見えた。 ImageImage
#統計 『統計学を哲学する』の著者の最大の問題点は、伝統的に言われていたり、社会的に制度化されてしまっているような事柄への、健全な批判精神に欠けることかもしれないと思いました。

次世代にクズをまとめて継承させるスタイル。
#統計 余談：Wilks' theoremの「近似的に従うχ²分布の自由度は包含関係にあるパラメータ空間の次元の差になる」というシンプルな結果を使えば、r×cの分割表の独立性検定での自由度が(r-1)(c-1)になることもすぐに出ます。

nbviewer.jupyter.org/gist/genkuroki…
#統計 余談：「自由度」を包含関係にあるパラメータ空間の次元の差(所謂「余次元」(codimension))と考えると良いことについては、私以外にも言っています。
#統計 余談: 帰無仮説によってパラメータ空間が何次元下がるかがそのまま「自由度」になります。2×2の分割表での各セルの期待値(パラメータとみなす)

α β
γ δ

について、独立性の帰無仮説は

αδ/(βγ) = 1

という条件で書け、この条件でパラメータ空間の次元は1下がるので自由度は1になる。
#統計 【Earman, 1992, pp.144-149】に何が書いてあるのか？

【分布族が対象を十全にモデル化】していなくても【ある弱い前提さえおけば、ベイズ流の更新プロセスは最終的に真理へと到達しうる】(p.83)とは書かれておらず、分布族と無関係にサイズ∞のデータによる真理到達の話が書かれていると予想。 Image
#統計 【分布族が対象を十全にモデル化】していなくても【ある弱い前提さえおけば、ベイズ流の更新プロセスは最終的に真理へと到達しうる】(p.83)は極めて驚くべき主張で、分布族のモデルを使ったベイズ更新によって到達可能なのはそのモデルで実現可能な最良の結果に過ぎません。 Image
#統計 最も簡単な場合として、未知の分布q(y)の無限に長い独立試行の結果Y_1, Y_2, Y_3, … (無限サイズのサンプル)が得られれば、未知の分布q(y)が未知ではなくなります。これは【分布族】ともベイズ 統計とも無関係。

Earman, 1992, pp.144-149を確認した人がいたら解説をお願いします。 Image
#統計 言うまでもないことですが、【分布族が対象を十全にモデル化】していなくても【ある弱い前提さえおけば、ベイズ流の更新プロセスは最終的に真理へと到達しうる】(p.83)は極めて驚くべき主張の「驚くべき主張」の意味は「驚くほどデタラメで非常識な主張」という意味です。 Image
#統計 分岐スレッド
#統計

「統計学はお墨付きを得るための道具ではない」は私の口癖の1つ
twilog.org/genkuroki/sear…

添付画像の引用は『統計学を哲学する』の最初の部分にあります。この部分にこの本の杜撰な解説が生じた理由が書いてあると私は思いました。続く Image
#統計 統計学について、地道な具体例の計算例(最もシンプルな場合であれば高校数学をマスターしていれば十分に可能、AICについてやって見せた！)を積み重ねて理解を深めれば、統計学ユーザーはギャンブルをやっていることになり、統計学は決して「お墨付き」が得られる道具ではないことがわかります。
#統計 麻雀のようなゲームで確率について一切気にしない人は確実に負け組になる。

限られたリソースの範囲内で勝ち目を増やしたいという理由で確率論を統計学の形式で利用することは合理的です。

しかし、それによって実際に勝ち目を増やせるかもしれませんが、真の「お墨付き」は決して得られない。
#統計 統計学のツールが前提としている条件が実際に成立しているかもよく分からないことが多いので、ユーザーは分野固有の専門知識をフルに使ってそのような事態にも備えておかなければいけない。

私は統計学を勉強して各分野固有の専門知識の重要性をより強く確信するようになりました。
#統計 以上のようなことを私は多分繰り返し述べている。

『統計学を哲学する』の立場はそれとは対照的。そのことは添付画像に引用したpp.1-2の部分を見れば分かる。

⓪③の部分では哲学の重要性を語り、①②では統計学の【お墨付き】を与えてくれる【特権的な役割】【特権的な機能】を強調している。 Image
#統計 私であれば、適切な統計処理によって結論にお墨付きが得られるという考え方は誤りである、と言い切ってしまうところを、【良かれ悪しかれ】という言い方で統計学が【お墨付き】を得るために誤用されていることを批判せずに、なし崩し的に、哲学の重要性の根拠として採用してしまっているのだ。 Image
#統計 統計学のツールはそれが前提としている条件が成立していない場合に適用すると無力になる場合がある。

実際には色々微妙で、教科書的な前提条件が成立していなくても、実践的には問題ない精度が出ている場合もある。

その辺はケース・バイ・ケースで判断してもらうしかない。

これが私の考え。
#統計 あと、ベイズ統計のツールが使えるための前提条件の中には、「事前分布を主観的確信の度合いであると考えている」の類は含まれていないことも強調しておく必要がある。

ベイズ統計についてデタラメを教える習慣が無くなればこの注意は必要無くなるかもしれませんが、現時点では必要。
#統計 「お墨付き」が決して得られないことを正直に強調しつつ、それが非常に面白い分野であることを一所懸命説明して、道具は正しく使うべきであることを強調したい人達の立場と、『統計学を哲学する』の立場は正反対であり、『統計学を哲学する』の立場は極めて有害であると私は考えています。
#統計 【良かれ悪しかれ】という言い方で、統計学はお墨付きを得るための道具ではないと言い切らずに、統計学の【特権的な機能】を哲学の重要性の根拠としてしまっている時点で、内容が杜撰になってしまうのは私には明らかなことに思えます。

このことに、最初のページを見たときに気付くべきだった！ Image
#統計 解析学を使うときに最も大事なことは「～という条件のもとで～と～は近似的に等しくなる」という関係に注意を払い続けることです。

これは統計学でも顕著です。
#統計 定義や由来になっている思想が異なる量A,B,C,…が応用先で成立している条件のもとで近似的に等しくなることすでに数学的に証明されているならば、A,B,C,…のどれを使っても結論はほぼ同じとしなければいけません。

この原則に矛盾する主義や思想は間違っているものとして捨て去らないとダメ。
#統計 ある条件のもとで、通常の仮説検定のP値とそのベイズ統計での対応物が近似的に等しくなることを示せる。そのような場合に、仮説検定とベイズ統計の主義思想が違うと言い張っても無益。

しかし、そういう場合に仮説検定を否定してベイズ統計を使えと主張するおバカさんもいる。
#統計 ある条件のもとで、最尤法とベイズ統計の結果がほぼ等しくなることを示せる。そのような場合にも、最尤法とベイズ統計は主義思想が異なると言い張っても詮無いことです。

添付画像はベルヌイ分布モデルの最尤法(上段)とベイズ統計(下段)に関するプロット。ほぼ同じ。

nbviewer.jupyter.org/gist/genkuroki… Image
#統計 数学的に証明された結果はどんなに喚いてもひっくり返せない。

ある条件のもとで近似的に等しくなることが証明されている2つに異なるツールをその条件が成立している場合に適用するときに、主義思想が違うという理由で結論を変えるようでは、科学的な議論をするつもりがないとみなされます。
#統計 道具A,B,Cの値が異なる領域にそれらを適用するときにも、主義思想をいきなり持って来てどれを使うべきであるかの結論を出すのは非科学的です。

例えば、以下のリンク先に引用した意味での「尤度原理」をいきなり持ち出すのは反則もいいところで、真面目に相手をできる議論にはなりようがない。
#統計 尤度のような数学的に正確に定義された道具を使用する場合には、その数学的性質についてよく理解し、その道具の適用が適切であるかを、尤度という道具が有用であるための数学的条件を応用先の状況が満たしているかについて最初に確認するべきなのです。
#統計 尤度の定義は「モデル内でデータと同じ数値が生じる確率(もしくは確率密度)」です。「モデルのデータへの適合度」の適切な指標の1つとみなせる。

だから、尤度を「モデルのデータへの適合度」の指標として利用することは、尤度の適切な使用の仕方です。続く
#統計 それを超えた目的のために尤度を使用する場合には、何か特別な条件が必要になります。

例えば、「モデルがデータに適合していること」と「モデルがデータを生成した法則の妥当なモデル化になっていること」は異なるので、後者の指標(もしくはその構成要素)として使用する場合には注意が必要。
#統計 データの生成法則をi.i.d.でモデル化することが妥当な場合には、モデルの側を固定してサンプルサイズnを無限に大きくすれば尤度(の対数の1/n倍)はモデルの「もっともらしさ」の正しい指標になるが、有限のnではそうではない。

この点は尤度ユーザーが最も注意するべきことです。
#統計 さらに、データとモデルの組から尤度函数を作ったときに、データの情報とモデルの情報が大幅に失われる点にも注意が必要です。

以下のリンク先で紹介した動画は非常に印象的です。

2次元の多変量正規分布モデルの尤度函数が動画中の異なるデータについて全部等しくなります。
#統計 私の経験では、尤度の持つ数学的性質について十分に理解することは相当に大変なことで難しい。

しかし、ひとたび尤度の数学的性質を理解してしまえば、尤度をどのように使うのが適切で、どう使うと不適切であるかは、常識的な考え方で容易に明らかになります。
#統計 尤度ユーザーになるために理解しておかなければいけない尤度の数学的性質を何もないところから全部一人で理解しようとするのは大変過ぎ。数学的事柄の理解は大変。私自身も苦労している。

しかし、尤度に関する雑談が普通にされているような文化に触れることができれば圧倒的に楽になるはず。
#統計 統計学の制度的な利用の仕方とか、過去に偉い人達が何を言っていたかではなく、現時点での最良の知識に基いて一貫した考え方を作り上げようとせずに、【統計学】で【お墨付き】が得られる現状をなし崩し的に当然の前提として【哲学】の重要性の根拠にしてしまっている時点でアウト。 Image
#統計 統計学はお墨付きを得るための道具ではない。
#統計 『統計学を哲学する』についてはこのツイートが連なる長大なスレッドが参考になると思います。
#統計 『統計学を哲学する』については、実は「文献を正しく引用しているか？」という点についても疑いを持っています。

文献を確認できていないので「疑い」の段階で止まっていますが、文献と独立に変なことが書いてあるのは確かなこと。

例えば添付画像中におけるEarman, 1992, pp.144-149の引用。 Image
#統計 【大本である分布族が対象を十全にモデル化していなければならない。この要請が満たされていなかったら～どうなるのか。実はその場合でも～ベイズ流の更新プロセスは最終的に真理へと到達しうる～(Earman, 1992, pp.144-149)】

もしもEarmanさんの本にこんなデタラメが書いてあったらびっくり！ Image
#統計 分布族をモデルとして与えたときにベイズ更新で到達できるのはその分布族で実現可能な最良の結果まで。一般には真理には到達しません。

Earmanさんは分布族によるモデル化と無関係にデータサイズ無限大の理想的な状況から得られる結論について書いているだけだと私は予想しています。
#統計 【大本である分布族が対象を十全にモデル化していなければならない。この要請が満たされていなかったら～どうなるのか。実はその場合でも～ベイズ流の更新プロセスは最終的に真理へと到達しうる】(p.83)はあまりにも非常識過ぎて、どうしてこんなデタラメを書けたのかが不思議なくらいです。
#統計 対象を十全にモデル化していない分布族を使ったベイズ更新であっても【ある弱い前提さえおけば】真理に到達できるなどと、どんな魔法なんだ、と言いたくなる。

独立の個人の説なら書いた本人が馬鹿扱いされて終わりですが、他人の本を引用してそちらにそう書いてあることをにおわす。ひどすぎ。 Image
#統計 それ一ヶ所だけに狂った考え方が書いてあるだけならば、笑いながら「正気であってもデタラメを書いちゃうことがあるよね」(笑)で済ませられますが、【確率変数が持つ分布を特徴付ける値を、その期待値～という】(p.31)と書いてあるページもあるし、他にもおかしなことが書いてある。笑えない。 ImageImageImage
#統計 これも既出だが、pp.144-145の説明も相当に奇妙です。AICについて理解している人が書くとは思えない説明の仕方。

しかも【より詳しい説明は久保(2012)を参照】と書いてある。

久保さんの本に本当にこんな説明があるの？

私には信じられない。

どなたか確認をよろしくお願いします。 Image
#統計 AICに興味がある人はツイッターの検索で最近の私の解説を読んだり、赤池弘次さん自身による1980年の論説

jstage.jst.go.jp/article/butsur…
エントロピーとモデルの尤度
日本物理学会誌35巻(1980)7号

を読んでおくと良いと思います。

赤池さんは実質的にSanovの定理を使って説明しています。 ImageImage
#統計 『統計学を哲学する』については「いいじゃないか、そんなにめくじらを立てなくても！」と感じる人は多いかもしれませんが、甘く見ない方が無難。

この手の本に手を出す人の多くは、最初に素晴らしい本だと言ってしまうと、その後はその意見を決して変えない。もしくは撤回せずに黙る(笑)
#統計 この本を誉めている人達は

【確率変数が持つ分布を特徴付ける値を、その期待値～という】(p.31)

【分布族が対象を十全にモデル化していなければならない】という要請が満たされていなくても【ベイズ流の更新プロセスは最終的に真理へと到達しうる】(p.83)

などのトンデモない説明を素通し。
#統計 『統計学を哲学する』には、サイズn=1000のデータから作った予測分布の平均対数尤度はその後毎年n=1000のデータを集めて平均したものだと書いてあるように見えます(笑)

予測分布を作るときに使うデータについての平均の話とは違うことに注意。

【久保(2012)】にそういう説明が書いてあるのか？ Image
#統計 p.17の図1.1に引用されているGaltonさんによるグラフは非常の教育的。

楕円の長軸と2つの回帰直線(2つのlocus of ～ tangent points)の違いと関係が明瞭なグラフを19世紀に描いてくれています。

『統計学を哲学する』では楕円の長軸を回帰直線だと説明していてすべてが台無しになっている。😅 Image
#統計 『統計学を哲学する』に好意的な人達の特徴は

【「Major axes」～が回帰直線】p.17

【確率変数が持つ分布を特徴付ける値を、その期待値～という】(p.31)

など(他にもたくさんある)の、統計学の詳細に関わるおかしな説明があることに触れずに、「主義」に関係した話題に終始すること。
#統計 おそらく、統計学の詳細に関わることは、「主義」の話をしたい人達にとっては、小さなどうでも良いことなのでしょう。

じきに「一流の学術誌にも主観主義のベイズ主義に基く論文が掲載されていること」を「主義」の重要性の根拠として持ち出す人が出て来るでしょう。

すでに出て来ているかも😱
#統計 じきに「一流の学術誌にも主観主義のベイズ主義に基く論文が掲載されていること」を「主義」の重要性の根拠として持ち出す人が出て来るでしょう、と書いたのですが、なるほど。

KLDはKullback-Leibler divergenceですかね。

なるほど、これはひどいな。 Image
ますます、かけ算順序問題に似て来た感じ。

かけ算順序指導を主導している算数教育専門家達がおかしな考え方をしていることを指摘しているときに、算数教育専門家がかけ算順序指導を積極的に押し進めているという事実を指摘して反論したつもりになるのは非常にまずい。
#統計 数学が絡みの話題においてテクニカルな事柄についての詳細を紹介するのは主に私だけになることが多い。

「主観確率」「ベイズ主義」「意思決定論」に基くベイズ統計の解釈のよくある解説についても私自身が詳しく紹介しており、そこでは「それ自体が不合理なわけではない」とまで言っている。
#統計 私による「主観確率」「ベイズ主義」「意思決定論」に基くベイズ統計の解釈の解説については以下のリンク先を参照。

これを理解してもらった方が、何が問題なのかが明瞭になると思う。

ちなみにKLD(笑)は「主観確率」「ベイズ主義」「意思決定論」に基くベイズ統計の解釈でも使用されます。
#統計 注3で【トップジャーナルとされる学術誌を見渡せば現実的に今でもベイズ主義流の合理的“信念の度合い”に基づく意思決定論を受け継いだ論文は容易に見つけられる】ことを根拠に持ち出す態度はあきれた態度だが、添付画像の青線の内側は良いと思いました。

gamp.ameblo.jp/yusaku-ohkubo/… Image
#統計

【確率変数が持つ分布を特徴付ける値を、その期待値～という】(p.31)

【分布族が対象を十全にモデル化していなければならない】という要請が満たされていなくても【ベイズ流の更新プロセスは最終的に真理へと到達しうる】(p.83)

などのトンデモない説明の素通しの実例がまた1つ増えた。
#統計 「尤度主義」(尤度原理)に関する杜撰な議論を平気でできる人達が結構いるということの再認識も今回のこの話題で再確認できました。

search.ameba.jp/search/entry/%…
#統計 実際には「頻度主義」「ベイズ主義」「尤度主義」などの「〇〇主義」という言葉自体がひどく曖昧で、批判側にそれを明確化するか負担が生じているのだ。

そういう負担が生じることを認識すれば、「主義にもとづく統計学」が「不倒の存在」である理由もすぐに分かります(笑)
#統計 『統計学を哲学する』における【尤度原理～とは仮説やパラメータの推論に関するすべての情報は観測されたデータに対する尤度関数のなかに含まれているとする主張】(p.123)は、「尤度原理」をクリアに定義してしまったせいで、それが馬鹿げた考え方であることが明瞭になっている珍しい例(笑)
#統計 データX_1,…,X_nと推測用モデルの確率分布族p(x|θ)に対して決まるパラメータθの函数

L(θ) = p(X_1|θ)…p(X_n|θ)

を尤度函数と呼びます。尤度函数で要約してしまうと、データとモデルの情報が大幅に失われる。

例：p(x|θ)が正規分布族ならデータの平均と分散だけで尤度函数が決まってしまう。
#統計

* データの情報だけからどれだけのことを推論・推測・推定できるかについて考えること

と

* データとモデルの情報を尤度函数で要約し、尤度函数だけで可能な推論・推測・推定を行うべきであるという主義(←これは馬鹿げている)

を明瞭に区別することが重要。当たり前。
#統計 統計学のテクニカルな詳細の説明の良し悪しを無視して、主に「主義」について語ることを好む学者達の存在は、統計学の理解と普及を妨害していると私も思っています。

統計学の発展が不幸な歴史的経路をたどったせいでそうなってしまっている感じ。
#統計 しかも、そこそこ知的な人達が、統計学におけるテクニカルな詳細よりも、統計学の世界にはびこる各種の「主義」に関する考察が知的であるかのように誤解することがあって、もはやどうにもならない感じ。
#統計 少し上で「尤度原理」(←馬鹿げている)について再度話題にしたので、『統計学を哲学する』における「尤度関数」の扱いがずさんであることも再度話題にしておきたいと思う。

尤度函数は【実際のデータの生成プロセス】と比較できるものではない。尤度函数と確率分布族を混同してはいけない。 ImageImageImage
#統計 例えば、正規分布族

p(x|θ) = exp(-(x-μ)²/(2σ²))/√(2πσ²), θ=(μ,σ²)

はパラメータθについては函数でxについては確率密度函数。

データX_1,…,X_nに関するその尤度函数

L(θ) = p(X_1|θ)…p(X_n|θ)

はパラメータθの函数。

これらは全然違うものです。明瞭に区別しなければいけない。
#統計 分布族と尤度函数の概念的区別さえ曖昧に書かれている本を読んで、統計学のイロハをまともに理解できるはずがない。

それ以前の問題として、【期待値】や【回帰直線】でさえ、一般読者は間違った知識をこの本から得てしまうことになります。

普通に読むに耐える質の本を作れなかったのか？
#統計 このスレッドの話題は、「主義」に関する話題と、「ずさんな説明の仕方」に関する話題の2つなのですが、途中から後者の比重が圧倒的に重くなって来ています。

現在は、「主義」の話題を好むことが、自然に「ずさんな説明の仕方」に繋がっているのではないか、と考えるようになって来ました。
#統計 統計学のテクニカルな詳細よりも統計学における「主義」を話題にしたがる傾向が、どのように「ずさんな考え方」に繋がって行くか？続く
#統計 まず杜撰になり難い考え方。

統計学の基礎になる複雑な数学的事柄を1つひとつ丹念に理解し、応用するときには、前提条件を応用先が満たしているかを常に確認し、数学的に出て来ないはずの結論を勝手に導き出さないようにする。

これを心掛けていればずさんになるのは難しい。続く
#統計 例えば、計算したP値が5%を切ったときには、「そのP値の計算に用いた前提のもとで、データ以上の偏りが生じるモデル内確率の近似値(すなわちP値)が5%未満になった」を超える結論に決して飛びつかない。

そして、飛び付く奴がいればその行為を批判する。続く
#統計 例えば、ベイズ 統計において、問題にしている事柄の事後分布で測った確率が大きくなったとしても、その確率はその計算に用いた前提のもとでのモデル内確率に過ぎないことを思い出し、問題にしている事柄の現実の確率が高くなったとは決して解釈しない。

そして、逆の行為を批判する。続く
#統計 数学的にどのような仮定のもとで何を計算したかをブラックボックスとして扱うのではなく、中身を精査して、その構成要素の各々の現実における妥当性を慎重に確認する、確認し切れなければ、確認し切れなかったことを正直に語る、などなどをやっていれば、ずさんな考え方には相当になり難い。続く
#統計 「複雑な数学的事柄を1つひとつ丹念に理解し、前提条件を応用先が満たしているかを常に確認し、数学的に出て来ないはずの結論を勝手に導き出さないようにする」ことをできていない人達がそうしない理由のことを「主義」と呼んでいるのであれば、「主義」に関する話は必ずずさんになるでしょう。
#統計 「複雑な数学的事柄を1つひとつ丹念に理解し、前提条件を応用先が満たしているかを常に確認し、数学的に出て来ないはずの結論を勝手に導き出さないようにする」ことをしっかりできていない段階で、「主義」だの「哲学」だの語り始めるようではダメだと思います。
#統計 私は統計学も勉強するようになって数学的教養が足りていないことを実感しました。「複雑な数学的事柄を1つひとつ丹念に理解すること」は大学学部での統計学入門レベルであっても容易なことではありません。解析学に関わる数学的厳密さの程度を大幅に落としてもそのことには変わりがありません。
#統計 現実には「お墨付きを得るための道具」として統計学が「制度的」に使われており、算数教育では悪名高い「きはじ図」のごとく統計学の「道具」が使用されており、悲惨なことになっている。

そういう現状に統計学の内容の説明が杜撰な『統計学を哲学する』と題された本が投入されたわけ。
#統計 そして、私が統計学について『統計学を哲学する』にどのような説明が書いてあるかを紹介しなかったとしたら、ツイッター上における「評判の良さ」をそのまま信じて、素晴らしい本だと思い続けた人達が結構多いんじゃないか？

これが実は今回の件で一番怖かったこと。
#統計 関連スレッド

以下のリンク先のスレッドではP値や信頼区間の解説をしている。
#統計 添付画像2,3は『統計学を哲学する』の最初の部分より。

その本は、統計学の不適切な使用法である「お墨付き」の取得を正当化するために使用可能な哲学っぽい俗説を真面目な哲学の話題として扱ってしまっている極めてずさんな内容の本だと私は考えています。続く ImageImageImage
#統計 実際には、標準的な事柄のまともな説明さえできておらず、どうしてこのような質の段階で出版されてしまったかについて疑問が出るような本になってしまっています。

この本を誉めている人達がこの本を順番に丁寧に読んだとは思えない。

例えば【期待値】【回帰直線】の説明が明らかにおかしい。 ImageImage
#統計 『統計学を哲学する』については、文献を正しく引用していないのではないかという疑いも持っています。

実際には、『統計学を哲学する』の著者が書いているようなことが書かれていない文献をあたかも書かれているかのように引用している可能性がある。

どなたか確認して下さると助かります。
#統計 『統計学を哲学する』については、その中に大量に含まれているずさんな記述をきちんと訂正した後でないと、著者が本当にやりたかったことへの評価は不可能でしょう。

個人的には読者に大量の自力訂正を要求するような本が出版された時点でアウトだと思います。
#統計 個人的に数学の本によくある式の誤植や書き間違いの類は大目に見るべきだと思います。

『統計学を哲学する』の場合はそういうケアレスミスとは異なる誤り(著者の理解不足を示唆する誤り)が多いという印象があり、文献の引用も自分が理解していないことの丸投げをやっている疑いさえある。
#統計学 以下のリンク先の話題に限らず、

【いずれの手法にも一長一短があり、データ解析者は、よりよい判断をくだすために、適用する手法の特徴を十分に理解し、データの様相をよく観察せねばならない】

というアドバイスは、

　安易に「主義」の話にしてはいけないこと

を含むと思います。
#統計学 各種の「主義」と無関係に確認できる統計学における数学的道具の性質をコンピュータの助けを借りて確認することによって理解を深め、自分が現在やっている仕事において、各方法がどのような長所と短所を持っていて、どれを選ぶと良さそうかについてはよく考えてみる。私はこれが普通だと思う。
#統計学 「主義」と無関係に確認できる各道具の数学的性質を確認せずに、各方法ごとに異なる「主義」や「思想」があるというような考え方に陥るとずさんでダメな考え方になってしまう。
#統計学 関連

ギャンブル(確率が絡むゲーム)での例えは多くの場合に適切。

統計学は決して「お墨付きを得るための道具」ではない。

社会的・制度的に「お墨付きを得るための道具」として使われてしまっていることは、「お墨付きを得るための道具」として適切であることを意味しない。
#統計 既出の添付画像は『統計学を哲学する』の本文の最初の部分より。

【良かれ悪しかれ、～】の部分は正しくは「悪しかれ悪しかれ」であり、【お墨付き】へのろくでもない期待における哲学の重要性について説明することを出発点にした時点で、非常にまずい方向に進んでしまっていると思う。 Image
#統計 『統計学を哲学する』のように【分布を特徴付ける値を、その期待値～という】とか【「Major axes」～が回帰直線】とか【分布族が対象を十全にモデル化して】いない場合でも【ベイズ流の更新プロセスは最終的に真理へと到達しうる】とか書いてある本に影響された人達は今後どうなって行くのか？ ImageImageImageImage
#統計 p.83の赤線の部分は『統計学を哲学する』の中の最悪の記述の1つです。

おそらくその本の著者は、

分布族と無関係に行われるデータによる信念の更新

と

「分布族の尤度函数と事前分布の積の正規化による事後分布の構成」の意味でのベイズ更新

の区別をうまくできていない。ひどすぎ。 Image
#統計 あとその本の著者は、モデルの分布族ではなくその尤度関数について【尤度関数が実際のデータ生成プロセスとは似ても似つかなかったら】という書き方をしていることから分かるように、モデルの分布族とその尤度函数の区別もうまくできていない。 Image
#統計 なによりも興味深い事実は、『統計学を哲学する』における統計学の説明が明らかにずさんであることを完全にスルーできる人達を発見することが容易なこと。

特に統計学をよく知らない人にはまともに読めるような質の本になっていないはずなのだが、どのように読めているのかが不思議。
#統計 常日頃「権威によって何が正しいかを判断する行為」を有害だと言っているのですが、現実には、名も地位もある立派な人達が(否定的でない)言及をしている本を、多くの人は読む価値のある本だとすぐに信じてしまう傾向は相当に強いです。

まずい本を他人に勧めた人達はどう責任を取るのか？
#統計

【分布を特徴付ける値を、その期待値～という】

とか😱

【「Major axes」～が回帰直線】

とか😱

【分布族が対象を十全にモデル化して】いない場合でも【ベイズ流の更新プロセスは最終的に真理へと到達しうる】

とか😱

なぜか毎年1000人のデータを集める話を始めちゃう

とか😱 ImageImageImageImage
#統計 確率分布族と尤度の区別が曖昧というのはまずいよな。統計学のイロハを全然分かっていない疑いさえある。その疑いは【分布を特徴付ける値を、その期待値～という】とか【「Major axes」～が回帰直線】の部分と整合的。

せめて、期待値や回帰直線の説明部分を出版前に訂正できなかったのか？
#統計 学生の人が『統計学を哲学する』を読んでいるのを発見したらちょっと慌てると思う。

こんなにひどい本を知的な本とみなして読んでしまい、いや、読んだつもりになり、ずさんな説明の存在に気付かずに終わるパターンに陥る可能性がかなりある。

ずさんな説明をきちっと批判できれば良いのだが。
私のように「確実にひどい本だろう」という確信を得たからこそ本屋で購入する人もいるだろうから、そう気にすることでもないか。

初歩的な点についてずさんな説明が明らかにあることを完全スルーして感想を述べている人達の方が大問題かも。

一言くらい訂正した方が良い点を指摘できないものか？
#統計 『統計学を哲学する』における統計学の解説がひどくずさんであることについては一致した評価になるべき。

「哲学」がらみの話題はずさんな説明を丁寧に否定・訂正した後にするべき。

他人にこの本を紹介する人は期待値や回帰直線の説明の訂正くらいはしてからにしないと問題があると思う。
#統計 私が強く疑っているのは、この本を褒めている人達は

* この本における統計学の解説部分に目を通していない

または

* 目を通していても統計学について無知過ぎて違和感さえ感じなかった

または

* 単にファッションとしてこの本を読んでいる

のどれかなのではないかということ。
#統計 良書が売れているのであれば素晴らしいことだが、【分布を特徴付ける値を、その期待値~という】(p.31)とか【「Major axes」～が回帰直線】(p.17)とか、【分布族が対象を十全にモデル化して】いない場合でも【ベイズ流の更新プロセスは最終的に真理へと到達しうる】(p.83)とか書いてある。酷い。 ImageImageImage
#統計

検定に関しても、「そのP値がどういう前提における何の数値であるか」に戻り、「そのP値の値だけから出て来るはずがない結論を出していないかどうか確認する」という作業を徹底的に行う前に、「Fisher流 vs. Neyman-Pearson流」の話を始めるようだとダメな議論になることが確定している。
#統計 「そのP値がどういう前提における何の数値であるか」を即答できてかつ、「そのP値の値から出せるはずがない結論」を十分に理解する努力をする前に、検定に関する「Fisher流 vs. Neyman-Pearson流」の話を考えようとする人達は、自分がいかにもダメなことをしていることを認識する必要がある。
#統計 私の経験では、統計学の勉強において「論争があった」という言葉を見たら、ほぼ間違いなくくだらない話で、「そのP値はどういう前提のもとでの何の数値であるか」の類の基本に戻って、昔あったらしい論争を無視して、常識に基いて何が言えるかを考えないと、ほぼ確実に誤解させられてしまう。
#統計 「主義」「思想」「論争」に関わる前にやるべきでかつやれる地道な理解のステップを飛ばす方向に誘惑して来る文献は要注意。
#統計 【分布を特徴付ける値を、その期待値~という】(p.31)とか【「Major axes」～が回帰直線】(p.17)と書いてある本が「新しい統計学の教科書」になってしまうようだとさすがにまずい。

哲学について語りたい人は、統計学に関するその手の杜撰な説明の存在にも必ず触れるべきだと思います。 ImageImageImage
#統計 相互リンク

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with 黒木玄 Gen Kuroki

黒木玄 Gen Kuroki Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @genkuroki

黒木玄 Gen Kuroki Profile picture
Jun 18, 2023
#統計 念の為のコメント

1️⃣「t検定の使用が適切なためには、母集団が正規分布に従っていることが必要である」という考え方は誤り。

2️⃣「Wilcoxonの順位和検定=Mann-WhitneyのU検定であれば、無条件使用は適切である」という考え方も誤り。

以上の誤りを信じている人達をよく見る。続く
#統計

1️⃣「t検定の使用が適切なためには、母集団が正規分布に従っていることが必要である」という考え方は誤り。

これについてはツイッター上で繰り返し非常に詳しく解説して来ました。

ツイログ検索
↓
twilog.togetter.com/genkuroki/sear…
#統計

2️⃣「Wilcoxonの順位和検定=Mann-WhitneyのU検定であれば、無条件使用は適切である」という考え方も誤り。

これについてもツイッター上で繰り返し非常に詳しく解説して来ました。

ツイログ検索
↓
twilog.togetter.com/genkuroki/sear…
Read 40 tweets
黒木玄 Gen Kuroki Profile picture
Jun 17, 2023
#数楽 ℤ[√2]やℤ[√3]はEuclid整域なのでPIDでUFDになるので、ℤ[√2]やℤ[√3]係数の多項式の √2や√3が出て来る因数分解の問題も既約元の積に分解する問題として意味を持ちます。続く
#数楽 ただし、整数dに関する√dが出て来る場合には、既約元の積への分解は因子の可逆元倍と順序の違いを無視しても一意的でなくなる場合が出て来ます。

実はそういうところに面白い数学が隠れている！
#数楽 整数の平方根が出て来る因数分解もちょっと話題になっていますが、その話はとてつもなく面白い数学の話に繋がっています！

中学生であっても思いつきそうな話の中にも素晴らしい数学が隠れています！
Read 20 tweets
黒木玄 Gen Kuroki Profile picture
Jun 16, 2023
東工大出身者のような理系の人達が、上野千鶴子が自閉症の母親原因説を唱えるくらい科学的に無能でかつ優しさに欠けた人物であることぐらいは知っておいた方が、我々の社会はよくなる可能性が高まると思います。

有名かつ有力になってしまった人物はたとえク○であっても無視できなくなる。
上野千鶴子は、自閉症の原因について母子密着説を唱えていたのですが、それが誤りであることが定説になっていることを指摘された後には、定説と上野千鶴子的なトンデモ説を平等に扱うという態度を取りました。

上野千鶴子の自分が苦しめた人達への態度は真にあきれるものでした。
上野千鶴子的な活動家は科学的無知と優しさに欠けた態度の両方の力を行使していました。

そういうことを許す伝統が現代においても人々の苦しみの源泉の1つになっているわけです。
Read 6 tweets
黒木玄 Gen Kuroki Profile picture
Jun 15, 2023
私は、環論を学ぶまで、重根もしくは重解の概念を十分に理解できた感じがしてなかったです。(代数)方程式の概念も同様。

実数体上の方程式x²=0は環

A = ℝ[x]/(x²)

で表現されます。これと方程式x=0に対応する環

ℝ[x]/(x)

は異なる。環論を使えば方程式x²=0とx=0を明瞭に区別できます。
環k上の環Aで表現された方程式のk上の環Bでの解集合はk上の環準同型全体の集合

Hom_{k-ring}(A, B)

で表現されます。例えば、集合として、

Hom_{ℝ-ring}(ℝ[x,y]/(x²+y²-1), ℝ) ≅ {(x,y)∈ℝ²|x²+y²=1}.
そして、以上のような代数方程式の表現になっている環の話について前もって知っておいた方が、環論の勉強はしやすいように思えます。
Read 6 tweets
黒木玄 Gen Kuroki Profile picture
Jun 15, 2023
以下のリンク先スレッド中にも書きましたが、

* 最初に共通の定数因子を括り出すと、その後の計算が楽になる場合がある。

と教えるようにして、

* 共通の定数因子を括り出していなくても、目くじらをたてない。

という教え方にすればよいと思いました。
教科書に従って「a(3x-6y)は誤りで、3a(x-2y)が正解だ」と安易に教えてしまった中学校の数学の先生は

　数学の先生なのに
　教科書通りにおかしなことを教えて
　ごめんなさい

と言って欲しいです。数学では教科書の内容を正しいと信じてはいけない。数学はそういうものだと大学で習っているはず。
数学を教えていれば、細かい条件を言い忘れるというような失敗は日常茶飯事のはずです。

人間だから仕方がないです。

大したことではないので、よりクリアになるように訂正すればよいと思います。
Read 18 tweets
黒木玄 Gen Kuroki Profile picture
Feb 22, 2023
#統計 speakerdeck.com/taka88/pzhi-fa… のp.7からp.8への流れは、natureの記事の内容を誤解させるような、よろしくない解説の仕方だと思いました。

「差がない」という特別な帰無仮説の検定だけで勝負を決めようとすることへの批判をP値そのものへの批判とみなすことは、よく見る杜撰な考え方です。続く
#統計 実際、natureの記事 nature.com/articles/d4158… ではcompati{ble,bility}が重要キーワードになっており、P値が

データ、モデル、パラメータ値のcompatibility(相性の良さ、両立性)の指標の1つ

とみなされることを詳しく説明しています。

この部分に触れずにこの記事を引用しても無意味。続く
#統計 natureのその記事を読んでいるならば、P値のcompatibilityとしての解釈について知り、添付画像のように、ダメな考え方と正しい考え方を区別できるようになっているはずなのです。

否定するべき対象にP値そのものが含まれていないことに注目！

続く
Read 13 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Don't want to be a Premium member but still want to support us?

Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal

Or Donate anonymously using crypto!

Ethereum

0xfe58350B80634f60Fa6Dc149a72b4DFbc17D341E copy

Bitcoin

3ATGMxNzCUFzxpMCHL5sWSt4DVtS8UqXpi copy

Thank you for your support!

Follow Us!

Send Email!

:(