Thread by @nickfismat

Thread sobre topologia? Oq encontro de conteúdo p quem não entende do assunto é sempre aquelas famosas imag… — Partiu #MatThreadBR curiouscat.qa/nickfismat/pos…

Existem duas palavras chave pra entender o que estuda a Topologia: continuidade e limites, então a gente vai precisar começar falando um tanto sobre isso

A noção mais simples de continuidade que a gente tem é a ideia de "Uma função que eu consigo desenhar sem tirar o lápis do papel"

Alguns exemplos são essas aqui

Isso era a noção que o pessoal usava uns séculos atrás, e dava pra dar conta do que eles precisavam. Porém, é uma noção meio pobre, no sentido de que você não consegue fazer muito com ela

O que significa conseguir desenhar a função sem tirar o lápis do papel? O que eu consigo deduzir disso?

Pior: essa função aqui, a função de Weierstrass, é contínua? Ela é fractal: sempre que você dá zoom em algum pedaço dela, tem mais dessa estrutura complicada

Eu garanto que ninguém consegue desenhar isso aí, independentemente de tirar o lápis do papel

Então o que a gente pode tentar fazer?

Bem, vamos olhar alguns exemplos de funções e ver quais a gente quer que sejam contínuas e quais a gente quer que sejam descontínuas

Essas aqui por exemplo. As vermelhas tem uma cara genérica do que a gente espera de uma função contínua e as azuis uma cara de descontínua

Como a gente pode descrever isso matematicamente?

Bem, a gente vê que, no caso das contínuas, quando a gente varia pouco o x, o f(x) varia pouco também. Já nas descontínuas, você mexe um pouquinho o x e o f(x) dá uns pulos, coisa desse tipo (tem outros tipos exemplos, mas vamos pensar assim por simplicidade)

Legal. Que diabos quer dizer "Variar um pouquinho"?

Nos números reais é rápido de responder:

Escolhe uma precisão ε > 0. Então tem algum δ tal que se eu tiver que |x-y| < δ, então vale que |f(x)-f(y)| < ε

Se eu quiser que f(x) e f(y) estejam a no máximo uma distância ε um do outro, é suficiente que x e y estejam a no máximo uma distância δ um do outro. Se eu deixar x e y perto o suficiente, f(x) e f(y) ficam arbitrariamente perto

Tudo isso é só um jeito chique de dizer "Se variar um pouquinho um x, você varia só um pouquinho o f(x)"

Aqui a gente tá usando "perto" ou "variar um pouquinho" no sentido do valor absoluto |x|. Isso funciona nos reais, mas e se eu quiser ir além?

Bem, em nenhum momento eu preciso do |x| na definição, eu só preciso de uma noção de distância. Em linguagem chique, eu preciso de uma métrica

A gente fala que uma função d: M x M -> IR (ou seja, uma função d(x,y) que come dois elementos de M e cospe um número real) é uma métrica se ela satisfizer algumas propriedades:

i. d(x,y) ≥ 0 pra todo x e y, com d(x,y) = 0 se, e somente se, x = y
ii. d(x,y) = d(y,x)
iii. d(x,y) ≤ d(x,z) + d(z,y)

i. quer dizer que distância nunca é negativa, e a distância entre dois pontos só é zero se forem o mesmo ponto
ii. quer dizer que a distância na volta é a mesma que na ida
iii. quer dizer que se você fizer um desvio no caminho, a distância não pode diminuir

Legal. Isso dá uma noção de distância e com isso a gente consegue trabalhar melhor aquela ideia de continuidade. Antes a gente só sabia se uma função é contínua se desse pra desenhar no papel. Agora a gente sabe em qualquer espaço que eu consiga medir distância

Dá pra melhorar?

Na verdade, dá! Como a gente mede distância? Usando aquela função d. Porém, falar que d(x,y) < r é a mesma coisa que falar que x tá dentro da bola com raio r centrada em y

É um jeito um pouco mais geométrico de pensar na mesma coisa

Ou seja, estar próximo significa estar dentro dos mesmos conjuntos! E conjuntos são muito mais gerais que distâncias! Em todo espaço eu consigo falar de conjuntos, com ou sem métrica

Então a gente usa essa ideia. Seja x um ponto aí. Eu vu dizer que uma sequência de pontos y_n tá se aproximando de x (tá tendendo a x) se pra todo conjunto A que contém x, existir algum N grandão tal que y_n tá em A pra todo n > N

Isso dá uma noção de proximidade que eu consigo fazer em qualquer espaço! Não preciso mais nem de métrica!

É... mas o mundo não é tão lindo né

Um dos conjuntos que contém x é o {x}. Então usando aquela definição, pra sequência y_n estar chegando perto do x, eventualmente ela precisa ser igual a x

Isso é meio merda, né?

Tipo, a sequência 1/n nunca chega no 0, mas claramente vai ficando mais perto dele... Você tem

1, 0.5, 0.3333, 0.25, 0.2, 0.166666, ...

Nunca é igual a zero, mas tá se aproximando...

Essa ideia de conjuntos é bacana, mas exigente demais!

Ao invés de pedir todos os conjuntos, vamos ser mais tranquilos e pedir só alguns

Como a gente decide quais pedir? Bem, vamos olhar os espaços métricos (aqueles com distância) e ver quais os conjuntos que a gente tava usando neles

Turns out que a gente tava usando uma coleção de conjuntos T com as seguintes propriedades:

i. O espaço todo e o vazio tão em T
ii. Qualquer união de elementos de T tá em T
iii. Intersecação de dois elementos de T tá em T

Então a gente vai fazer o seguinte: dado um conjunto X, a gente pega um conjunto de subconjuntos de X, que a gente vai chamar de T, e pensa no parzinho (X,T)

A gente não tá mais usando distâncias, mas precisa ter esse T

O T é o que a gente chama de topologia. É uma coleção de conjuntos que te dá uma noção extremamente simples e primitiva de distância. É muito mais geral que uma métrica porque a gente não tem mais um número medindo a distância. Eu só sei dizer se os pontos tão mais ou menos perto

É tipo a ideia de um termoscópio: um termômetro sem escala. Você não consegue medir a distância, mas você sabe dizer se x ou y que tá mais perto de z (bem, nem sempre: às vezes não dá pra decidir)

Essa é a ideia geral de topologia: estudar de forma extremamente geral o que significa estar próximo, o que significa uma função ser contínua, coisas assim

Isso tem implicações bem legais. O exemplo da caneca e da rosquinha é porque você consegue deformar um no outro continuamente: sem cortar nem colar pedaços, você consegue ir amassando a caneca até se tornar uma rosquinha

Agora vamos justificar o "fismat" no meu username e transformar isso continuamente numa #FísicaThreadBR: como essas coisas são interessantes em Física?

Eu vou primeiro ser cara de pau e puxar uma #AstroThreadBr e falar de Relatividade Geral: topologia é um dos principais ingredientes de Relatividade, buracos negros e tudo que gravita!

Uma das bases de Relatividade é exatamente você ter uma noção de como mapear o espaço-tempo. Em cada regiãozinha do espaço-tempo, você ter quer um jeito de colocar coordenadas nele (uma temporal e três espaciais) pra descrever onde e quando alguma coisa acontece

Por exemplo, você quer ser capaz de dizer "A lâmpada acendeu na posição (1,2,3) aos 4 segundos". O Universo não liga pra essas coisas, a gente que enfia coordenadas em tudo, mas pra isso o espaço-tempo precisa ser modelado de um jeito compatível

A saber, Relatividade Geral considera o espaço-tempo como uma variedade topológica com algumas propriedades a mais. "Variedade topológica" já sugere que a gente tem uma topologia, então alguma noção de proximidade

O resto que falta pra ser uma variedade topológica é que, em cada pedacinho, o espaço-tempo se parece com o IR^4: a gente consegue mapear com 4 coordenadas

Talvez você não consiga mapear o espaço-tempo inteiro, mas consegue fazer em pedacinhos. É que nem mapear a Terra: você não consegue fazer um mapa plano da Terra inteira, mas consegue fazer um da África, um da Ásia, um da Europa, etc, e juntar tudo num atlas

Além disso, a gente assume que as propriedades topológicas do espaço-tempo são bonitinhas: uma sequência y_n não pode se aproximar de dois pontos ao mesmo tempo (você consegue distinguir pontos diferentes) e coisas desse tipo

Isso é pra ilustrar que Topologia aparece na parte "fácil" de Relatividade, mas não para aí! Topologia tá levando um monte de prêmio Nobel de Física nesses últimos anos!

Incluindo, mas não limitado, a metade do Prêmio Nobel de Física de 2020! O Roger Penrose ganhou metade do Nobel desse ano por ter mostrado que buracos negros são uma previsão robusta da Relatividade Geral

Hoje em dia o resultado é conhecido como Teorema de Singularidade de Penrose. A grosso modo, ele diz que a formação de buracos negros a partir de colapso gravitacional de estrelas morrendo, por exemplo, não é uma questão de sorte. Acontece pra valer

Pra mostrar isso, ele usou técnicas de Topologia Diferencial. Relatividade costuma usar muitas ideias de Geometria Diferencial, que explora os aspectos mais locais da Topologia. Porém, a topologia é uma propriedade do espaço como um todo, não só desse ou daquele pedacinho

O Penrose explorou esses aspectos e usou eles pra mostrar que os buracos negros realmente se formam. Depois o Hawking explorou as mesmas ideias rodando de trás pra frente no tempo pra mostrar que a previsão do Big Bang também é robusta (embora o Penrose não seja fã de BB xD)

Achou que eu só tinha um exemplo de Topologia ganhando Nobel de Física? ACHOU ERRADO

Nobel de 2016: Kosterlitz, Thouless, Haldane e transições de fase topológicas em Matéria Condensada

Vou ser honesto: eu não manjo de matéria condensada e não vou tentar falar sobre transição de fase de Kosterlitz-Thouless, mas eu ainda não terminei de brincar com topologia e vou sim dar as ideias gerais do que aparecem aí

Imagina que você tem um campo - uma função - definida em uma dimensão e que nas pontas ele assume valores +1 ou -1. Aqui tem alguns desenhos de como ele pode se parecer

Em termos topológicos, só tem três configurações distintas aí, porque eu posso deformar uma dessas aqui na outra continuamente. Em termos de Teoria Quântica de Campos, você consegue deformar uma na outra com uma quantidade finita de energia

Essas duas aqui não são equivalentes. Pra eu deformar uma na outra, eu precisaria levantar infinitos pontos do campo, e abrindo as contas bonitinho você descobre que isso gasta uma quantidade infinita de energia

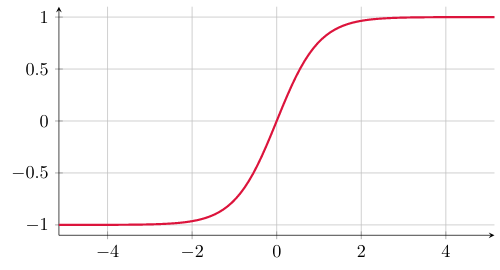
Em outras palavras, a topologia tá te impedindo de pegar uma configuração de campo e transformar na outra, porque no processo você precisaria de energia infinita. Ou seja, essas configurações são estáveis

Se você tiver um campo assim, por mais esquisito que ele pareça, ele não vai colapsar pra um valor constante

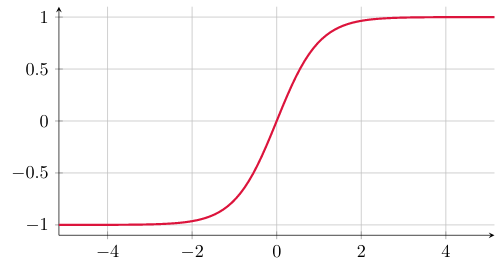
Isso funciona bem em uma dimensão espacial. Se colocar mais dimensões espaciais isso deixa de funcionar e você só tem soluções triviais (todas elas podem ser deformadas pra uma constante). Esse resultado chama Teorema de Derrick

Isso é um exemplo de um no-go theorem: um teorema dizendo que os físicos não podem fazer tal coisa. Físicos não gostam disso, então quando aparece um no-go theorem o pessoal começa a tentar driblar

E conseguiram! Esse problema de não ter soluções topologicalemente legais só existe se o campo estiver ali sozinho, mas todo mundo merece um amigo (Bob Ross style)

Adiciona um campo de gauge no meio e dá pra resolver

"Um campo de gauge" soa meio esquisito, mas não é: campos de gauge são partículas que transportam as interações principais que a gente vê no universo, como o fóton (eletromagnetismo), os bósons W e Z (interações fracas) e os glúons (interações fortes)

Pros interessados, aqui tem uma revisão sobre essas interações e sobre Grande Unificação (que por sinal, é pra onde a gente tá caminhando hehehehehe)

https://twitter.com/nickfismat/status/1341085803074740227?s=20

Na presença de um campo de gauge (como os que você tem em teorias de Grande Unificação) associado a um grupo SU(N) que quebra pra U(1), você pode usar argumentos parecidos pra chegar na existência de monopolos magnéticos

que merda isso quer dizer?

Tô falando SU(N) pra não ser tão geral quanto poderia. A grosso modo, se você tiver uma teoria que usa matrizes pra descrever as interações de gauge e uma dessas interações é o eletromagnetismo, essas questões topológicas dão origem a monopolos magnéticos

Você tem efeitos topológicos que tão fazendo aparecer um fenômeno que tem carga magnética sem ter carga elétrica. Isso encaixa super bem no Eletromagnetismo de Maxwell e explicaria porque a carga elétrica é quantizada, mas a gente nunca viu um

Mas o que você tem aqui é a topologia (que coisa, não?) usando essas ideias de deformação e coisa assim pra te dizer que você tem uma coisa que parece uma partícula com carga magnética se mexendo por aí

Isso pq a energia daquele campo estranho de antes (vermelho) é dada por uma curva parecia com essa azul: é um caroço de energia se mexendo pelo mundo!

Caroços de energia se mexendo por aí são essencialmente o que a gente entende como partículas, mas esse cara aí tem origem completamente topológica!

Mais do que isso, se você fizer as contas com carinho, você percebe que o caroço de energia na sua teoria com um campo de gauge e etc emite um campo magnético radial. É o que a gente esperaria de um monopolo

Monopolos magnéticos são uma das coisas mais fodas que eu já ouvi falar em Física, mas até hoje a gente não observou nenhum. Não é sem motivo, tho: nesse esquema topológico, que a gente chama de monopolo e 't Hooft-Polyakov, a massa dele é na ordem de 11 TeV

11 Tev são umas 100 vezes a massa do bóson de Higgs, que já foi difícil pra caramba de detectar. Você precisa de MUITA energia pra ver uma coisa assim!

Mas bem, quem sabe em breve? O pessoal tá querendo construir aceleradores de partículas ainda maiores (e se isso é uma boa ideia fica pra outro dia). Talvez daqui a alguns anos a gente veja o nosso primeiro monopolo

Agora que eu cheguei ao final, vou ser honesto e dizer que eu me empolguei pra falar de vários assuntos que tão bem na fronteira do meu conhecimento aushaushaush

Aqui vão algumas referências pros curiosos (como sempre, os acertos são deles, os erros são meus)

Teoremas de Singularidade de Penrose:

Vou deixar um vídeo de divulgação, mas textos clássicos de GR costumam falar sobre (não vou citar pq eu nunca estudei direito e não falei muito aqui)

-

Topological Field Theory e Monopolos Magnéticos:

- Zee, A. Quantum Field Theory in a Nutshell (Princeton: Princeton University Press, 2010)
- Lancaster, T. & Blundell, S. J. Quantum Field Theory for the Gifted Amateur (Oxford: Oxford University Press, 2014)

- 't Hooft, G. Magnetic Monopoles in Unified Gauge Theories. Nuclear Physics B79 (1974) 276--284

Topologia Geral:

Modéstia à parte, vou deixar minhas anotações de Topologia aqui. As referências delas são as referências originais minhas uahausaausha

- fma.if.usp.br/~nickolas/pdf/…

Bem, eu certamente me empolguei e quis brincar com assuntos de Física que estão (como eu disse) bem na fronteira do meu conhecimento (na real, são as últimas três aulas de Campos II do IFUSP, e duas delas eu ainda não assisti com calma uasaushaush)

De todo modo, fiquem à vontade pra perguntar e coisas do tipo. Como eu me animei em certo ponto é capaz que uns trechos tenham ficado mais complicados do que deveriam