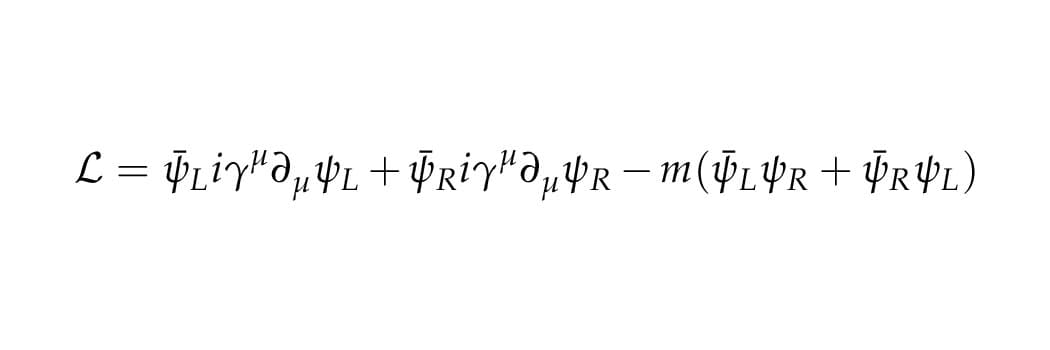Thread by @nickfismat

Se ninguém perguntou até agora,eu pergunto:
Oq diabos seria esse “mecanismo da gangorra” da última thread(m… — #FísicaThreadBR (e obrigadíssimo pelo elogio =D) curiouscat.qa/nickfismat/pos…

O tema de hoje é o mecanismo de gangorra (seesaw mechanism) pra massas de neutrinos. Eu vou voltar essa discussão mais pros lados da thread que eu fiz há uns dias sobre Teorias de Grande Unificação

https://twitter.com/nickfismat/status/1341085803074740227?s=20

Se antes de começar você quer ter uma ideia de como a gente sabe que os neutrinos tem massa, eu falei disso nessa outra thread aqui

https://twitter.com/nickfismat/status/1341604148383510529?s=20

Falar de neutrinos envolve falar de Física de Partículas, que é uma das muitas áreas da Física que mistura Mecânica Quântica e Relatividade Restrita. Então vamos começar falando um pouco de Mec Quântica Relativística

Ali pelo começo/metade do século XX, o pessoal tava tentando juntar MQ e Relatividade Restrita, duas teorias TOP do começo do século, de um jeito que fizesse algum sentido

Um dos primeiros passos desse processo foi obter a chamada Equação de Klein-Gordon, que é essa equação aqui

Esse \phi (a bolinha cortada) representa a função de onda de uma partícula: grosso modo, é um número complexo que depende da posição e do tempo e que se vc calcular o módulo ao quadrado dá a densidade de probabilidade de encontrar a partícula

Ok, vamo falar em língua de gente

Essencialmente, é uma função que te permite calcular a probabilidade de encontrar a partícula em um certo lugar e em um certo instante

A Equação de Klein-Gordon é relativística, mas a gente também tinha uma versão não-relativística: a equação de Schrödinger

Esse d/dt (com d esquisitio) e esse triângulo ao quadrado da Eq de Schrodinger tão meio escondidos dentro do d^2 que tinha na Eq de Klein-Gordon (vou chamar de EKG, já que somos íntimos)

Mas tem uma diferença problemática

Aquele d^2 da EKG tá ao quadrado, enquanto o d/dt de Schrödinger não tá

Esses d e d/dt são derivadas: eles representam a variação do que quer que elas estejam derivando com relação a alguma coisa. Na EKG, com relação ao espaço-tempo como um todo (o espaço tá no triângulo da Eq de Schrödinger). Na eq de Schrödinger, o d/dt se refere ao tempo (t)

Em Schrödinger, você deriva com relação ao tempo uma vez. Na EKG, deriva duas vezes

Isso é um problema

Quando você deriva uma vez só, pra resolver a equação você precisa fornecer uma condição inicial: como o sistema começou?

Em Schrödinger, você fornece só uma função \phi(x,0) (tempo 0) e tá feito. Dá pra resolver. A função de onda conta tudo sobre o sistema num dado tempo

Em KG, você tem duas derivadas, e por isso precisa dar duas funções. Geralmente a gente vai dar \phi(x,0) e d\phi/dt (x, 0), por exemplo. A função e o como ela tá mudando logo no começo (como se fosse, >>>a bem grosso modo<<<, a posição e a velocidade iniciais)

Isso é uma diferença brutal entre Schr&odinger e KG: em Schrödinger, a função de onda diz _tudo_, mas em KG você precisa dar a função de onda e algo a mais

Não gostei dessa história não. Vamo fazer alguma coisa diferente

Muito antes de mim, alguém bem mais esperto do que eu (não é difícil) ficou incomodado com isso e decidiu resolver. Esse era o Dirac

Ele propôs uma equação assim

Esse i é o mesmo da Eq de Schrodinger, o m é o mesmo das duas equações de antes (a massa da partícula), os d_\mu representam derivadas no espaço-tempo e esses \gamma^\mu são coeficientes que a gente precisa determinar

Essa é a forma mais geral que a equação poderia ter. Por enquanto, é só um chute tão amplo quanto possível

Então falta determinar esses coeficientes aí. Que diabos eles são?

Bem, números eles não podem ser. Se os \gamma^\mu fossem números, eles iam apontar em alguma direção no espaço-tempo, que ia ser privilegiada. Até onde a gente sabe, o Universo não privilegia nenhuma direção no espaço-tempo, então isso não pode ser

Brincando um pouco com a cara dessa equação (não vou entrar nos detalhes, mas essencialmente você quer mostrar que ela dá parecido com KG), a gente descobre que precisam ser matrizes 4x4

Brincando mais com essa equação e as matrizes 4x4, você eventualmente descobre que essa equação descreve muito bem os férmions: ela prevê que você tá estudando uma partícula que tem spin 1/2

Spin é momento angular intrínseco: dá pra pensar, a grosso modo, que é como se a partícula estivesse girando. Grosso modo pq a partícula é pontual e ponto não gira, mas ela se comporta de um jeito como se tivesse girando

Não vou dar muita ênfase no 1/2 pq ele não vai ser importante a nível de divulgação (a nível mais técnico, ele justifica toda essa discussão auhsaus), a menos do fato que 1/2 é diferente de 0

Bacana, a gente tem então a Eq de Dirac, excelente pra descrever férmions. Inclusive, é com ela mesmo que a gente estuda quarks, elétrons e cia. ltda., por exemplo

Fast forward em vários anos de Física, a gente descobriu que MQR na real é uma coisa bem esquisita e dá muito problema, eventualmente decidindo abandonar em prol do que a gente chama de Teoria Quântica de Campos. Os detalhes das diferenças ficam pra outro dia (me cobrem auhsaush)

Pra tentar vocês a me cobrar, MQR prevê o próprio fim: ela é inconsistente com as próprias previsões. TQC resolve essas inconsistências ao custo de muitas ideias novas (e interessantíssimas)

Em particular, em TQC a gente quase nunca lida com as coisas tentando resolver essa ou aquela equação. As técnicas ficam diferentes e é mais conveniente expressar a Física por meio de uma Lagrangeana

Eu adoro a ideia de Lagrangeana: é uma função que codifica toda a Física do sistema. Como as partículas se movem, como interagem e tudo mais. Quer colocar uma nova interação? Soma um termo!

A Lagrangeana que descreve a equação de Dirac é essa aqui

Esse \psi com uma barra tá relacionado ao \psi usual. É como se fosse o conjugado complexo (bem, é isso mesmo, mas tbm tem uma transposição de matriz e multiplica pela matriz \gamma^0 à direita (detalhes))

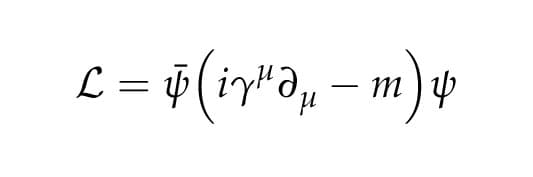
Dá pra escrever isso de um jeito mais conveniente

Lembra que eu comentei que o importante sobre spin pra gente era que 1/2 é diferente de 0? Pois é

A gente sabe que o férmion tá sempre "girando" com spin 1/2. Ele pode estar girando pra esquerda ou pra direita. A gente chama isso de helicidade

Se ele gira do mesmo jeito que os dedos da sua mão direita, onde o dedão aponta na direção que ele tá andando, a gente fala que é de mão-direita. Do contrário, mão-esquerda

Como isso depende de pra onde ele tá se mexendo, depende de referencial. Alguém que tá andando mais rápido que um férmion de mão-direita vai ver ele como sendo de mão-esquerda

Porém, a gente consegue definir um conceito parecido, chamado quiralidade, que não tem esse problema de depender de referencial, e ele coincide com a helicidade pra partículas sem massa

Tudo isso pra falar: a gente pode descrever em separado a parte do férmion que gira pra esquerda e a que gira pra direita

Aquele psi tinha 4 componentes (afinal, ele tava sendo multiplicado pelas matrizes gamma, que são 4x4). A parte esquerda vai ter 2 e a direita outras 2

Isso parece meio bobo, né? Pq alguém ia querer fazer isso?

De modo curto: porque as interações fracas (que são responsáveis por decaimentos e coisas do tipo) tratam férmions de mão-esquerda e de mão-direita de jeitos diferentes

As interações fracas gostam muito mais de férmions de mão-esquerda. Em particular, no Modelo Padrão, você tem um neutrino de mão-esquerda, mas o neutrino de mão-direita não interage com ninguém

No que tange o Modelo Padrão, ele essencialmente não existe

Dito isso, separando em esquerda (L = left) e direita (R = right), a Lagrangeana de Dirac vira

Os termos com as gammas e as derivadas descrevem como os férmions se mexem. A gente chama de termos cinéticos. O outro pedaço, que tem o m, é o termo de massa

A gente não vai mexer no termo de massa, então eu não vou ficar escrevendo ele. A gente tá interessado nesse pedaço aqui

A história não acaba aí. Eventualmente, o Majorana percebeu que a Eq de Dirac não era a única possibilidade pra descrever os férmions. Também dava pra tentar algo assim:

Hoje em dia essa aí é a Equação de Majorana. Esse \psi_c é um conjugado de carga do \psi: é trocar o férmion pelo antiférmion. Troca o elétron pelo pósitron, o quark pelo antiquark, o neutrino pelo antineutrino

Isso dá problema pra vários férmions: se o férmion tiver carga (como o elétron, os quarks, etc), o \psi e o \psi_c tem cargas elétricas diferentes, então não rola

Mas se o férmion for neutro...

Pro neutrino, essa equação pode funcionar muito bem! Comparando com a eq de Dirac, a gente vê que o termo cinético é exatamente igual, a única diferença é o termo de massa

Vale mencionar ainda que se \psi é de mão-esquerda, \psi_c é de mão-direita. Colocar o c troca a orientação

Dito isso, o termo de massa de Majorana vai ser assim

Esse C grandão é uma matriz que aparece na definição do \psi_c. Dessa vez eu escrevi o c em cima por conveniência (na real eu esqueci de conferir a consistência da notação antes de postar o tweet de antes, mas detalhes)

No caso, essa equação aí é pro neutrino de mão-direita, que não aparece no Modelo Padrão (\psi_L^c é de mão direita). Tbm dá pra escrever pro de mão-esquerda (só tirar os c dos \psi), mas o mecanismo de gangorra que eu quero mostrar não usa isso

As fórmulas tão ficando complicadas, então vamos dar uma pausa e lembrar um pouco das coisas de Grande Unificação que eu falei na outra thread

O mais importante era: dá pra enfiar o Modelo Padrão dentro de uma teoria maior baseada num tal de grupo SU(5) - que a gente discutiu bastante

Além disso, dá pra enfiar o SU(5) dentro de uma teoria maior, com o SO(10)

https://twitter.com/nickfismat/status/1341100194839089153?s=20

O que eu não contei é que quando você coloca o SU(5) dentro do SO(10), você consegue colocar todos os férmions do Modelo Padrão, mas sobra um lugar vazio pra alguém que não interage com SU(5)

E quem não interage com SU(5) e a fortiori não interage com o Modelo Padrão??

O neutrino de mão-direita!

Como em SO(10) apareceu um neutrino de mão-direita, a gente pode colocar uns termos dele no meio da Lagrangeana

É como eu tinha falado: quer colocar uma interação nova? Põe um termo a mais!

No caso, a gente quer dar massa pro neutrino. Podemos escolher entre Majorana, Dirac ou só misturar os dois =)

Como o neutrino de mão-direita não interage com ninguém, a gente consegue colocar um termo de Majorana igual o que eu escrevi agora há pouco

Esse vai dar uma massa que a gente vai denotar por M. Como ele é "transparente" pro SU(5), essa massa tem que ser por volta da energia em que o SU(5) vale. Olhando na thread de antes, isso é pelo menos umas 10¹¹ vezes a massa do bóson Z

https://twitter.com/nickfismat/status/1341101120689741824?s=20

Além disso, a gente pode usar o neutrino de mão-direita pra colocar uma massa de Dirac, m, no neutrino. O termo de Dirac quebra a simetria SU(2) x U(1). Isso é um jeito desnecessariamente complicado de falar que m tem que ser perto da massa dos quarks e léptons

Por completeza, a massa do elétron (que é um lépton), é por volta de m_e ~ 5.6 x 10⁻⁶ M_Z (ou seja, bem mais leve que o bóson Z)

O que importa é: m é leve, mas perto da massa do elétron, enquanto M é pesado pra caralho (tipo, PESADO MESMO)

Massa de Majorana pro neutrino be like:

Juntando os dois termos, a gente fica com uma expressão assim pro trecho de massa de neutrinos da Lagrangeana

Vc tem ali as massas de Dirac, m, e a de Majorana, M. O h.c. no final quer dizer "Eu sei que o que eu escrevi é um número complexo e devia ser um número real. Soma o conjugado pra resolver esse problema" (é mais fácil escrever h.c. do que o conjugado)

Dessa vez eu escrevi \nu ao invés de \psi pq a gente tá interessado só nos neutrinos mesmo

A matriz no meio descreve como são as massas dos neutrinos. Se ela fosse diagonal, o neutrino (1 0) ia ter a massa no canto superior esquerdo e o (0 1) ia ter a do canto inferior esquerdo. Porém, ela não é diagonal

Isso é mais uma vez a história da superposição. Eu discuti isso em um contexto um pouco diferente na outra thread de neutrinos

https://twitter.com/nickfismat/status/1341607054092476416?s=20

Pra conseguir ler as massas dos neutrinos, a gente precisa achar quais são as setinhas diagonais que correspondem a estados com massa definida. Os neutrinos de mão-esquerda e direita não tem massa definida. Os neutrinos de massa definida não tem mão definida

Se você fizer as contas, você vai descobrir que, como M >> m, os neutrinos com massa definida respeitam isso aqui

O primeiro estado de massa definida, \nu_1, é uma setinha diagonal que tá QUASE deitada. Na prática, é essencialmente um neutrino de mão-esquerda. A massa é da ordem de m^2/M

O segundo estado, \nu_2, é uma setinha diagonal que tá QUASE em pé. É essencialmente um neutrino de mão-direita. A massa é da ordem de M

Agora lembra que m era leve e M era pesadão? Isso quer dizer que m^2/M é MUITO leve. Extremamente leve

Assim como os neutrinos de mão-esquerda que a gente observa na natureza

Por outro lado, M era super pesado, e portanto o neutrino de mão-direita tá saindo muito pesado dessa história

Isso explicaria porque a gente não vê neutrinos de mão-direita dando sopa: eles são muito pesados, e você precisa de muita energia pra ver partículas pesadas

Em particular (hehe), os experimentos que a gente tem chegam a cerca de 100 M_Z e olhe lá. O neutrino de mão direita precisaria de pelo menos 100 000 000 000 M_Z

É. Falta um pouco

Isso é (um exemplo de) o que a gente chama de mecanismo de gangorra (seesaw mechanism): você tem um neutrino super pesadão que deixa o outro super levinho

Claro, uma coisa importante: essa explicação de pq a gente não vê o neutrino de mão-direita, pq o neutrino é tão leve e tudo mais é só uma hipótese. Isso tudo ainda é um problema aberto em Física de Partículas e o que eu tô mostrando é só um dos jeitos que você pode abordar

Outras opções são colocar só a massa de Dirac (faz M=0 naquela matriz), só a de Majorana (m=0), colocar um termo de Majorana pro neutrino de mão-esquerda (troca aquele 0 da matriz por um M_L) e por aí vai

Qual opção tá certa? Ninguém sabe. Já faz uns vinte e tantos anos que a gente sabe que os neutrinos tem massa, mas até hoje a gente não faz ideia de como são essas massas

E é aí que você entra ;D

Por fim, vou deixar aqui minhas referências principais pra essa thread. Como usual, os acertos são deles, os erros são meus

Mecânica Quântica Relativística

Essa parte na real eu fiz de cabeça, mas vou deixar uma sugestão de leitura

- Greiner, W. Relativistic Quantum Mechanics: Wave Equations (Berlin: Springer, 1995)

TQC & Física de Neutrinos

- Langacker, P. The Standard Model and Beyond (Boca Raton: Taylor & Francis, 2017)
- Zee, A. Quantum Field Theory in a Nutshell (Princeton: Princeton University Press,
2010)

~TQC eu tbm fiz de memória, mas o Zee é uma referência excelente