#Julia言語 Julia言語で10行
nbviewer.jupyter.org/gist/genkuroki…
(1/5) 二項分布モデル内の標本分布で測った95%信頼区間にモデルのパラメーター値が含まれる確率のプロット。95%以上になる。ほとんどのパラメーターで95%より真に大きい。
nbviewer.jupyter.org/gist/genkuroki…
(1/5) 二項分布モデル内の標本分布で測った95%信頼区間にモデルのパラメーター値が含まれる確率のプロット。95%以上になる。ほとんどのパラメーターで95%より真に大きい。
https://twitter.com/genkuroki/status/1371684833949192198

#Julia言語
nbviewer.jupyter.org/gist/genkuroki…
(2/5) 二項分布モデルの95%信頼区間 [CI_min, CI_max] を平面上の座標 (CI_min, CI_max) にプロット。丸の大きさはモデル内でその信頼区間が生じる確率の大きさに比例。赤の十字の左上側の領域ではパラメータの真の値が信頼区間に含まれている。
nbviewer.jupyter.org/gist/genkuroki…
(2/5) 二項分布モデルの95%信頼区間 [CI_min, CI_max] を平面上の座標 (CI_min, CI_max) にプロット。丸の大きさはモデル内でその信頼区間が生じる確率の大きさに比例。赤の十字の左上側の領域ではパラメータの真の値が信頼区間に含まれている。

#Julia言語
nbviewer.jupyter.org/gist/genkuroki…
(5/5) Kuramoto model! 初期条件も周期も異なる振動子が互いの相互作用によって「ほぼ同期」するようになる。繰り返しになるが、各枡目に配置された振動子の周期は互いに異なる。それでも同期する方向の相互作用が十分に強ければ同期するようになる。
nbviewer.jupyter.org/gist/genkuroki…
(5/5) Kuramoto model! 初期条件も周期も異なる振動子が互いの相互作用によって「ほぼ同期」するようになる。繰り返しになるが、各枡目に配置された振動子の周期は互いに異なる。それでも同期する方向の相互作用が十分に強ければ同期するようになる。

#Julia言語 続き。Kuramoto model の動画。
こういう動画も10行で作れる。
訂正:1つ前のツイートの添付画像の Printf を削除。それは余計。
using Distributions, DifferentialEquations, Plots の3つのパッケージを使った自然な10行のコードでKuramoto modelの動画を作れる!
こういう動画も10行で作れる。
訂正:1つ前のツイートの添付画像の Printf を削除。それは余計。
using Distributions, DifferentialEquations, Plots の3つのパッケージを使った自然な10行のコードでKuramoto modelの動画を作れる!
#Julia言語 あ、動画中の3-dimensional の綴りもおかしい!もとのソースコードどその結果の方
nbviewer.jupyter.org/gist/genkuroki…
は今から直しておきます。
nbviewer.jupyter.org/gist/genkuroki…
は今から直しておきます。
#Julia言語 視力の問題でこういうことになっている。こういうミスは今後増える一方になると思う。
#Julia言語 以下のリンク先のプロットは初めて作った。他の人で同様のグラフを作った人がいるかどうかは知らない。
信頼区間を平面上の点(丸)としてプロットしている。丸の大きさはモデル内標本分布で生じる確率の大きさに比例。
個人的にこれを見て少し理解が深まった。
信頼区間を平面上の点(丸)としてプロットしている。丸の大きさはモデル内標本分布で生じる確率の大きさに比例。
個人的にこれを見て少し理解が深まった。
https://twitter.com/genkuroki/status/1371793783109521410
#Julia言語
nbviewer.jupyter.org/gist/genkuroki…
(3/5) 3次元ランダムウォークの動画を作り直した。
ランダムウォーク自体は1行で作れます。
それの動画を作るコードの方がずっと長くなる。
それでも全部でぴったり10行におさまった。
nbviewer.jupyter.org/gist/genkuroki…
(3/5) 3次元ランダムウォークの動画を作り直した。
ランダムウォーク自体は1行で作れます。
それの動画を作るコードの方がずっと長くなる。
それでも全部でぴったり10行におさまった。
#Julia言語 Kuramoto model の動画を再掲。
マス目の個数は16×32=512個ある。
個数を4倍にした32×64=2048個の場合も楽勝で計算できたが、動画のサイズも増えたので、この程度にした。
ソースコード↓ (10行しかありません)
nbviewer.jupyter.org/gist/genkuroki…
マス目の個数は16×32=512個ある。
個数を4倍にした32×64=2048個の場合も楽勝で計算できたが、動画のサイズも増えたので、この程度にした。
ソースコード↓ (10行しかありません)
nbviewer.jupyter.org/gist/genkuroki…
#Julia言語 以下のリンク先は空行を除いて9行
微分方程式のソルバはシンプレクティック法の1つであるYoshida6()で、微分方程式のパラメータに幅を持たせた場合の影響を視覚化しています。
こういうのも10行必要ない。
微分方程式のソルバはシンプレクティック法の1つであるYoshida6()で、微分方程式のパラメータに幅を持たせた場合の影響を視覚化しています。
こういうのも10行必要ない。
https://twitter.com/genkuroki/status/1371652699930853377
#Julia言語 #数楽 Kuramoto model には相互作用の強さを表すパラメータKが入っていて、Kがある値K_cを超えると急激に同期が強まる(相転移が起きる)ことが知られています。
添付画像
Kuramoto model: K = 0.9K_c の場合
同期は起こらない。
添付画像
Kuramoto model: K = 0.9K_c の場合
同期は起こらない。
#Julia言語 #数楽
Kuramoto model: K = 1.3K_c の場合
「すべての2つの枡目の組み合わせ」で相互作用が起こっています。各人が残りの全員の状態に引っ張られている。
そのひっぱりの強さがある一定以上にならないと同期は起こらない。
Kuramoto model: K = 1.3K_c の場合
「すべての2つの枡目の組み合わせ」で相互作用が起こっています。各人が残りの全員の状態に引っ張られている。
そのひっぱりの強さがある一定以上にならないと同期は起こらない。
#Julia言語 以上のような計算機実験がJuliaを使えばたったの10行のコードを書くだけで可能です。
ソースコードを見れば、どのような微分方程式を考えているかや、臨界値 K_c の値がどのように決まっているかもわかる。
ソースコード↓
nbviewer.jupyter.org/gist/genkuroki…
ソースコードを見れば、どのような微分方程式を考えているかや、臨界値 K_c の値がどのように決まっているかもわかる。
ソースコード↓
nbviewer.jupyter.org/gist/genkuroki…

#Julia言語 ソースコード解説
1. パッケージの読み込み
2~3. 蔵本モデルの微分方程式の記述
dθ_i/dt = ω_i + K (1/N) Σ_j sin(θ_j - θ_i) (i=1,…,N)
θ_iはi番目の振動の角度による表現。
θ_iはmod 2πでのみ意味を持つ。
ω_iはデフォルトの角速度。iごとに違う。
Kは相互作用の強さを表す。
1. パッケージの読み込み
2~3. 蔵本モデルの微分方程式の記述
dθ_i/dt = ω_i + K (1/N) Σ_j sin(θ_j - θ_i) (i=1,…,N)
θ_iはi番目の振動の角度による表現。
θ_iはmod 2πでのみ意味を持つ。
ω_iはデフォルトの角速度。iごとに違う。
Kは相互作用の強さを表す。

#Julia言語
4. パラメータの設定
* m×nで表示
* d = ω_iのばらつき方を記述する平均0標準偏差2の正規分布
* v = ω_iの期待値
* K_c = 2/(π p(0)) (p(x)は左右対称な分布dの密度函数)。同期が始まる臨界値K_cはデフォルトの角速度ω_i達のばらつき方が大きいほど大きくなります。直観的には当然。
4. パラメータの設定
* m×nで表示
* d = ω_iのばらつき方を記述する平均0標準偏差2の正規分布
* v = ω_iの期待値
* K_c = 2/(π p(0)) (p(x)は左右対称な分布dの密度函数)。同期が始まる臨界値K_cはデフォルトの角速度ω_i達のばらつき方が大きいほど大きくなります。直観的には当然。

#Julia言語 続き
* tmax = どの時刻まで計算するか
* a = 1.3 相互作用の強さ。後で相互作用の強さKをK=aK_cと定める。
5. モデルのパラメータ
θ₀ = θ_i達の初期値をランダムに決める
tspan = (0.0, tmax)
K = aK_c
ω = ω_i達を平均vばらつき方dでランダムに決める
続く
* tmax = どの時刻まで計算するか
* a = 1.3 相互作用の強さ。後で相互作用の強さKをK=aK_cと定める。
5. モデルのパラメータ
θ₀ = θ_i達の初期値をランダムに決める
tspan = (0.0, tmax)
K = aK_c
ω = ω_i達を平均vばらつき方dでランダムに決める
続く

#Julia言語 続き
6. 微分方程式の数値解 sol を求める
7~10. sol からgif動画を作成。
JuliaのPlots.jlによるgif動画の作成はmatplotlibによるgif動画の作成よりもずっとシンプルで簡単です。
以前はmatplotlibでgif動画を作っていたのですが、Plots.jlに完全に引っ越してしまいました。
6. 微分方程式の数値解 sol を求める
7~10. sol からgif動画を作成。
JuliaのPlots.jlによるgif動画の作成はmatplotlibによるgif動画の作成よりもずっとシンプルで簡単です。
以前はmatplotlibでgif動画を作っていたのですが、Plots.jlに完全に引っ越してしまいました。

#Julia言語 モデルのコード化には、微分方程式、パラメータ、初期値などを全部書く必要があります。その分だけの行数はどうしても必要。使用するパッケージの読み込みの行も必要です。これで6行消費。
残りの4行でgif動画作成。(最後のendを1つ前の行の行末に移動すれば全部で9行に減らせる)
残りの4行でgif動画作成。(最後のendを1つ前の行の行末に移動すれば全部で9行に減らせる)

#Julia言語 ほど、パッケージの読み込みとモデルの記述だけで微分方程式の数値解が求まってしまいます。視覚化の見栄えを良くするための工夫もシンプルに書けている。圧縮して書いているのにコードの可読性はそう悪くない。
こういう使い方をするにはJuliaは最強の道具だと言ってよいと私は思う。
こういう使い方をするにはJuliaは最強の道具だと言ってよいと私は思う。

#Julia言語 DifferentialEquations.jlで求めた数値解 sol はこの場合には時刻 t のm×n行列値函数としての機能も持っていて、非常に便利です!
sol(t)はθ_i(t)達のm×n行列で、sin.(sol(t)) は sin(θ_i(t)) 達のm×n行列になります。sin.(sol(t))' はその転置になる。そのヒートマップを作画している。
sol(t)はθ_i(t)達のm×n行列で、sin.(sol(t)) は sin(θ_i(t)) 達のm×n行列になります。sin.(sol(t))' はその転置になる。そのヒートマップを作画している。

#Julia言語 私は数日前のnightly buildを使っています。
DifferentialEquations.jlを使う場合には「Julia v1.6以上推奨」ということにしておいた方が多分よいです。最初の読み込みにかかる時間がv1.5だと無駄に長くなってしまいます。
DifferentialEquations.jlを使う場合には「Julia v1.6以上推奨」ということにしておいた方が多分よいです。最初の読み込みにかかる時間がv1.5だと無駄に長くなってしまいます。
#Julia言語 Plutoノートブックも用意しました。添付画像のようなことをできます。
gist.github.com/genkuroki/a50f…
以下のリンク先と同様の方法で上のリンク先のURLをPlutoで貼り付ければ使えます。ただし、
pkg> add DifferentialEquations
も忘れずに。

gist.github.com/genkuroki/a50f…
以下のリンク先と同様の方法で上のリンク先のURLをPlutoで貼り付ければ使えます。ただし、
pkg> add DifferentialEquations
も忘れずに。
https://twitter.com/genkuroki/status/1371113291460710403
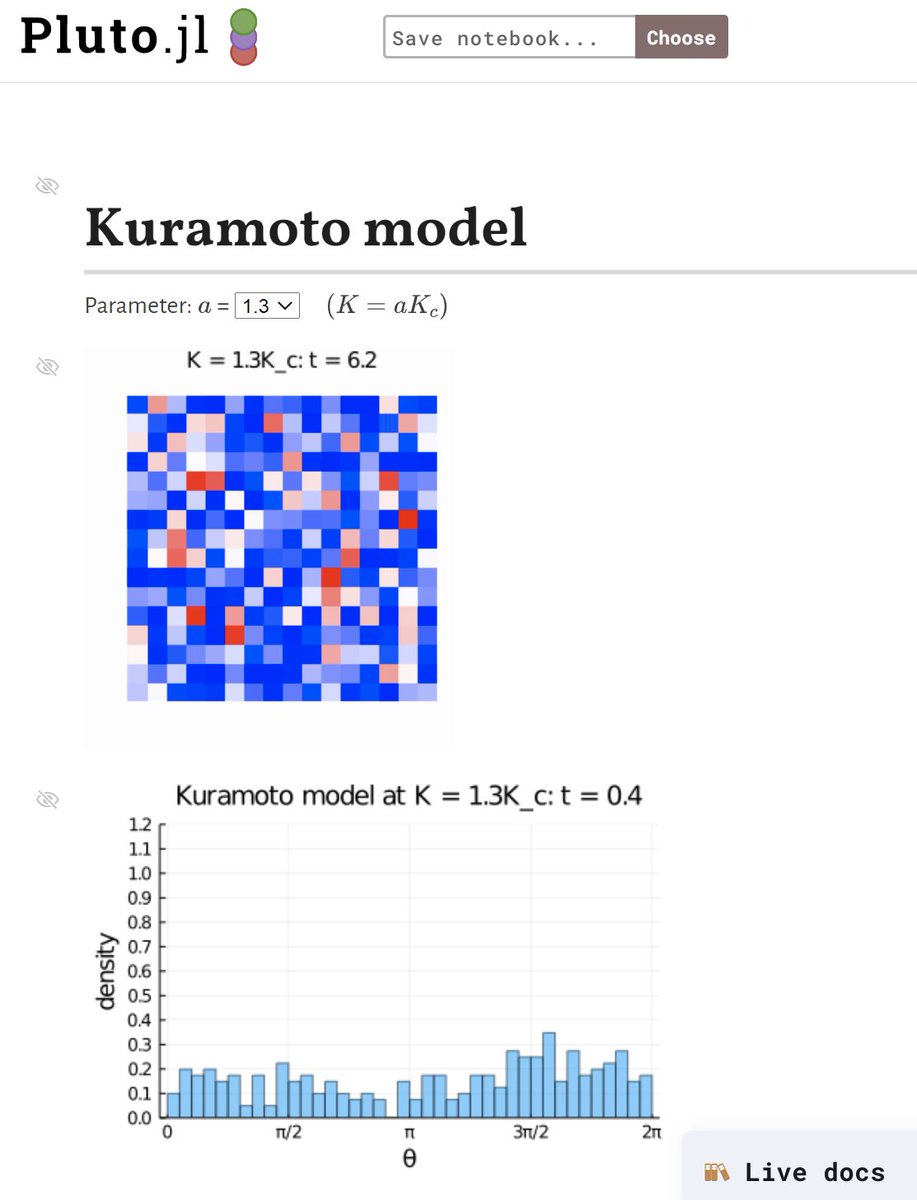
#Julia言語 #数楽
1つ前のツイートの場合(K = 2K_c)におけるθ_i達の分布の動画。
初期条件は一様分布。
各θ_iごとに相互作用無しのときのデフォルトの周期は違う。異なる周期を持つ振動子であっても、蔵本モデルではこのように同期してしまう。
1つ前のツイートの場合(K = 2K_c)におけるθ_i達の分布の動画。
初期条件は一様分布。
各θ_iごとに相互作用無しのときのデフォルトの周期は違う。異なる周期を持つ振動子であっても、蔵本モデルではこのように同期してしまう。
#Julia言語
DifferentialEquations.jl はものすごく便利。例えば数値解が「函数」の形式で得られる!(こういうインターフェースが定義されているのは本当にありがたい)
しかし、Julia v1.5以下だとusingにかかる時間が長い。Julia v1.6以上で使うことがお勧め。
nightly buildでも使えています。
DifferentialEquations.jl はものすごく便利。例えば数値解が「函数」の形式で得られる!(こういうインターフェースが定義されているのは本当にありがたい)
しかし、Julia v1.5以下だとusingにかかる時間が長い。Julia v1.6以上で使うことがお勧め。
nightly buildでも使えています。
#Julia言語 添付画像のように、v1.5.4と数日前のnightly build (v1.6以上でもほぼ同じはず)では、最初のusingにかかる時間が全然違う。
一度、v1.6以上の世界に慣れると、もうv1.5には戻れなくなります(笑)
Juliaを使い続けると大体数ヶ月ごとに「前よりも使い易くなった」と感じることができます。
一度、v1.6以上の世界に慣れると、もうv1.5には戻れなくなります(笑)
Juliaを使い続けると大体数ヶ月ごとに「前よりも使い易くなった」と感じることができます。

#Julia言語 継続的な改善を「学習」してしまうとどうなってしまうか?
①試しにnightly buildも使ってみようと思うようになる。
②nightly buildはひどく壊れていることがある。
③そのとき、「学習」の効果によって、「大きな改善が約束されていることを意味する」と感じるようになる(笑)
①試しにnightly buildも使ってみようと思うようになる。
②nightly buildはひどく壊れていることがある。
③そのとき、「学習」の効果によって、「大きな改善が約束されていることを意味する」と感じるようになる(笑)
#Julia言語 現在では(相対的に)nightly buildもかなり安定しているし、壊れているnightly buildにぶちあたっても、壊れていない段階のnightly buildに戻せば使い続けられます。
#Julia言語 はバイナリもまとめて面倒をみてくれるパッケージマネージャーが優秀なので、実験的に新しいバージョンを入れてみることへの心理的障壁が低いです。
自分専用のパッケージ集の大規模破壊の心配がほぼない。
Pythonでは何度もやらかしたことがある。
自分専用のパッケージ集の大規模破壊の心配がほぼない。
Pythonでは何度もやらかしたことがある。
#Julia言語 以下のリンク先のP値を扱うコードは書き直した。現在のバージョン
nbviewer.jupyter.org/gist/genkuroki…
ならv1.5.4でも動きます。
nightly buildでは
range(a, b; length=n)
の代わりに
range(a, b, n)
と書けるようになっています。それを上の形式に戻した。

nbviewer.jupyter.org/gist/genkuroki…
ならv1.5.4でも動きます。
nightly buildでは
range(a, b; length=n)
の代わりに
range(a, b, n)
と書けるようになっています。それを上の形式に戻した。
https://twitter.com/genkuroki/status/1371793118203322374

#Julia言語 #数楽
⪅(x, y) = x < y || x ≈ y
pval(d, k) = sum(pdf(d, j) for j in support(d) if pdf(d, j) ⪅ pdf(d, k))
は普遍的な「一次元有限離散分布dとデータkのP値を求める函数」の定義になっています。例えばdとして二項分布や超幾何分布を使える。
⪅(x, y) = x < y || x ≈ y
pval(d, k) = sum(pdf(d, j) for j in support(d) if pdf(d, j) ⪅ pdf(d, k))
は普遍的な「一次元有限離散分布dとデータkのP値を求める函数」の定義になっています。例えばdとして二項分布や超幾何分布を使える。

#Julia言語 ⪅(x, y) = x < y || x ≈ y は離散分布を浮動小数点数で扱うときにはほぼ必須の函数です。
理論的には x ≤ y という比較で十分であっても、浮動小数点数 x, y の計算では、x > y となっていても、"x ≤ y" とみなさなければいけない場合が出て来ます。
⪅ は x ⪅ y の形式で使えます。
理論的には x ≤ y という比較で十分であっても、浮動小数点数 x, y の計算では、x > y となっていても、"x ≤ y" とみなさなければいけない場合が出て来ます。
⪅ は x ⪅ y の形式で使えます。
#Julia言語
pval(d, k) = sum(pdf(d, j) for j in support(d) if pdf(d, j) ⪅ pdf(d, k))
は分布dとデータkについて「分布d内でデータk以上に生じ難いjのどれかが分布d内で生じる確率」です。
生じ難さで「偏り」を測るときの「モデル内でデータ以上の偏りが生じる確率」=P値の定義そのもの。
pval(d, k) = sum(pdf(d, j) for j in support(d) if pdf(d, j) ⪅ pdf(d, k))
は分布dとデータkについて「分布d内でデータk以上に生じ難いjのどれかが分布d内で生じる確率」です。
生じ難さで「偏り」を測るときの「モデル内でデータ以上の偏りが生じる確率」=P値の定義そのもの。
#Julia言語 「定義に戻って数学的にシンプルに考える」をできている人にとってJuliaは天国で、定義に戻ってシンプルに考えた式をそのままJulia語に直せば計算したいものが計算できてしまいます。
P値はブラックボックス扱いするべき数値ではなく、各場合ごとに自分で定義を考えるべき類のものです。
P値はブラックボックス扱いするべき数値ではなく、各場合ごとに自分で定義を考えるべき類のものです。
#Julia言語 d = Binomial(n, p) のとき、データkに関するpの信頼区間はP値がα以上になるpの集合のことです(これが定義)。データkが分布dで生成されているとき、pがその信頼区間に含まれる確率は
prob_ci_contains_p(d, α=0.05) = sum(pdf(d, k) for k in support(d) if pval(d, k) ≥ α)
prob_ci_contains_p(d, α=0.05) = sum(pdf(d, k) for k in support(d) if pval(d, k) ≥ α)
#Julia言語 P値やモデルのパラメータ値が信頼区間に含まれる確率は1行で定義された函数で計算できる!
しかも、そうした方が可読性が高くなる!
それらの函数は、英単語の意味を知っていれば、Juliaを知らなくても何を計算しているかがわかるように書ける。
これが抽象化の威力です。
しかも、そうした方が可読性が高くなる!
それらの函数は、英単語の意味を知っていれば、Juliaを知らなくても何を計算しているかがわかるように書ける。
これが抽象化の威力です。

#Julia言語 「二項分布モデルでモデルのパラメータの値が95%信頼区間に含まれる確率を計算してプロットしなさい」という練習問題を解いておくことは、信頼区間ユーザーになりたい人にとって必須だと思います。
JuliaならばP値函数の実装も自分で行ってもそれの問題を10行で解けてしまうわけです。
JuliaならばP値函数の実装も自分で行ってもそれの問題を10行で解けてしまうわけです。

#Julia言語 JuliaのDistributions.jlでは「確率分布」をJuliaの変数dに格納できます。確率分布をdの1文字で表現し、その確率密度函数もpdf(d, x)と書ける。
Distributions.jlでは「確率分布」の概念がきちんと抽象化されている。そういうことができているならJulia以外でも同様のことをできます。
Distributions.jlでは「確率分布」の概念がきちんと抽象化されている。そういうことができているならJulia以外でも同様のことをできます。
#Julia言語 添付画像中では二項分布での信頼区間を計算する函数が2行で書けています。通常の書き方をすると、
function ci(n, k, α)
CI = find_zeros(p -> pval(Binomial(n, p), k) - α, 0, 1);
k == 0 ? (0.0, CI[end]) : k == n ? (CI[1], 1.0) : (CI[1], CI[end]))
end
くそシンプル!
function ci(n, k, α)
CI = find_zeros(p -> pval(Binomial(n, p), k) - α, 0, 1);
k == 0 ? (0.0, CI[end]) : k == n ? (CI[1], 1.0) : (CI[1], CI[end]))
end
くそシンプル!
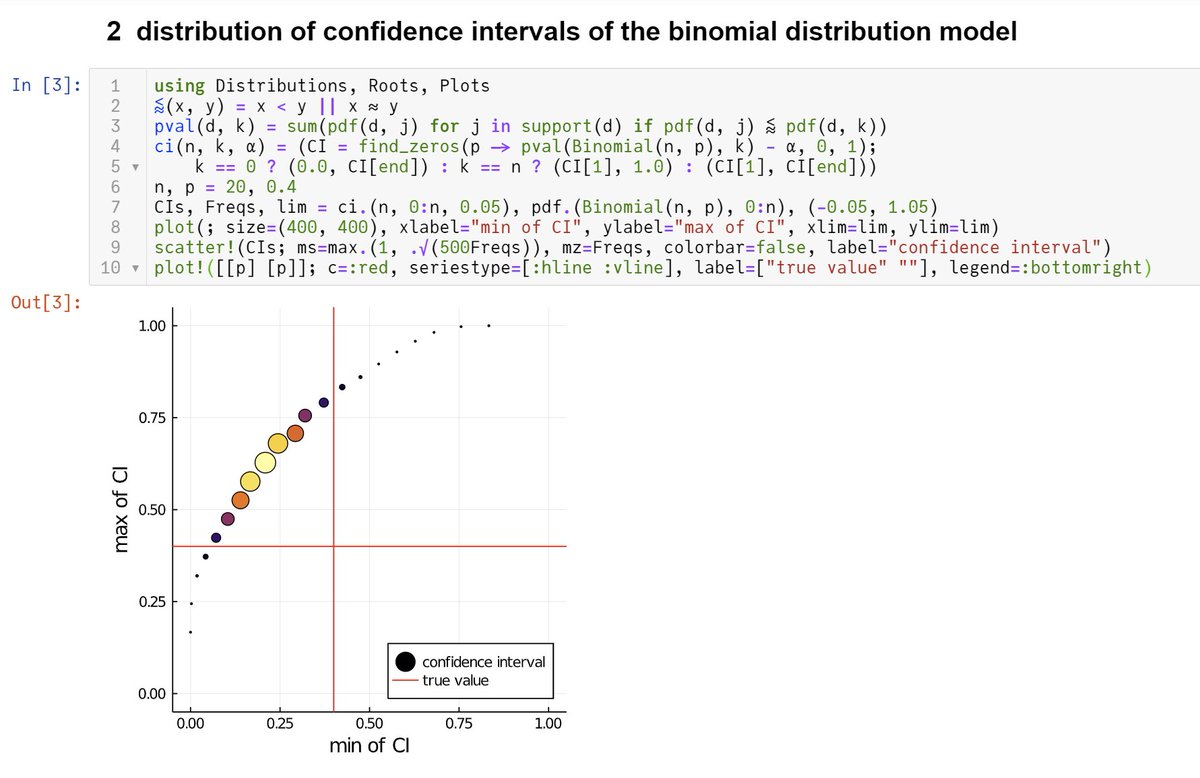
#Julia言語 find_zeros(f, a, b) は区間[a, b]内での函数fの零点の全体を配列で返してくれる函数です。
函数 f(p) = pval(Binomial(n, p), k) - α の零点は二項分布モデルのP値がαになるパラメーターpの値のことで、それらを求めることは信頼区間の計算そのものになっています。
函数 f(p) = pval(Binomial(n, p), k) - α の零点は二項分布モデルのP値がαになるパラメーターpの値のことで、それらを求めることは信頼区間の計算そのものになっています。
#Julia言語 後で数値積分ライブラリを使うことになるとしても、簡単な数値積分函数を自分で書いてみるという経験は大事。
オイラー法さえ自分で実装したことがない人が、微分方程式のソルバのライブラリを使うのは危険だと思う。
自分でP値や信頼区間を計算する函数を書く経験もあった方がよい。
オイラー法さえ自分で実装したことがない人が、微分方程式のソルバのライブラリを使うのは危険だと思う。
自分でP値や信頼区間を計算する函数を書く経験もあった方がよい。
#Julia言語 上の方で二項分布モデルのP値と信頼区間の1~2行による実装法を解説したが、2×2の分割表の独立性に関するFisher検定のP値も信頼区間も1~2行で書ける。
しかもそうやって実装した結果はRのfisher.testよりも良い性質を持っていたりする。
ソースコード↓
nbviewer.jupyter.org/gist/genkuroki…



しかもそうやって実装した結果はRのfisher.testよりも良い性質を持っていたりする。
ソースコード↓
nbviewer.jupyter.org/gist/genkuroki…




#Julia言語
Julia集合の動画も10行で作れる。
余裕のプログレスメーター付き(笑)
どこまで進んだかを表示させたい人には参考になるはず。
(Mandelbrot集合の動画も同様の方法で作れるはず)
ソースコード↓
nbviewer.jupyter.org/gist/genkuroki…
Julia集合の動画も10行で作れる。
余裕のプログレスメーター付き(笑)
どこまで進んだかを表示させたい人には参考になるはず。
(Mandelbrot集合の動画も同様の方法で作れるはず)
ソースコード↓
nbviewer.jupyter.org/gist/genkuroki…

#Julia言語 でJulia集合の動画を作成
ソースコード↓
nbviewer.jupyter.org/gist/genkuroki…
この手の作品では色の付け方が結構重要なポイントになることが多い。これはカラーマップとして:gist_earthを使っている。
この手のことも全部10行で可能。この場合には余裕でプログレスメーターも設置できた。
ソースコード↓
nbviewer.jupyter.org/gist/genkuroki…
この手の作品では色の付け方が結構重要なポイントになることが多い。これはカラーマップとして:gist_earthを使っている。
この手のことも全部10行で可能。この場合には余裕でプログレスメーターも設置できた。
#Julia言語 信頼区間函数をもっとまともなものにした。
二項分布モデルの場合
function ci(n, k, α)
CI = find_zeros(p -> pval(Binomial(n, p), k) - α, 0, 1)
isone(length(CI)) ?
CI[1] < 0.5 ? (0.0, CI[1]) : (CI[1], 1.0) : (CI[1], CI[end]))
end
nbviewer.jupyter.org/gist/genkuroki…

二項分布モデルの場合
function ci(n, k, α)
CI = find_zeros(p -> pval(Binomial(n, p), k) - α, 0, 1)
isone(length(CI)) ?
CI[1] < 0.5 ? (0.0, CI[1]) : (CI[1], 1.0) : (CI[1], CI[end]))
end
nbviewer.jupyter.org/gist/genkuroki…


#Julia言語
Julia語の
sum(f(x) for x in X if cond(x))
は数学語の
Σ_{x∈X with cond(x)} f(x)
に直訳できる。
Pythonから来た人が sum([f(x) for x in X if cond(x)]) のように余計な [ ] を追加しているのをよく見るが、[ ] は必要ないし、計算効率を落とすのでやめた方がよい。
Julia語の
sum(f(x) for x in X if cond(x))
は数学語の
Σ_{x∈X with cond(x)} f(x)
に直訳できる。
Pythonから来た人が sum([f(x) for x in X if cond(x)]) のように余計な [ ] を追加しているのをよく見るが、[ ] は必要ないし、計算効率を落とすのでやめた方がよい。
https://twitter.com/genkuroki/status/1372051934337634305

#Julia言語 こういう動画を10行で作れます。
何百行もあるコードだと解読する気になれなくても、たったの10行ならば解読する気になれるかも。実際に解読できれば、こういうことを自分で自由にできるようになる。
ソースコード↓
nbviewer.jupyter.org/gist/genkuroki…
何百行もあるコードだと解読する気になれなくても、たったの10行ならば解読する気になれるかも。実際に解読できれば、こういうことを自分で自由にできるようになる。
ソースコード↓
nbviewer.jupyter.org/gist/genkuroki…
#Julia言語 Mandelbrot set animation 作り直し
#Julia言語
10行シリーズ全ソースコード↓
nbviewer.jupyter.org/gist/genkuroki…
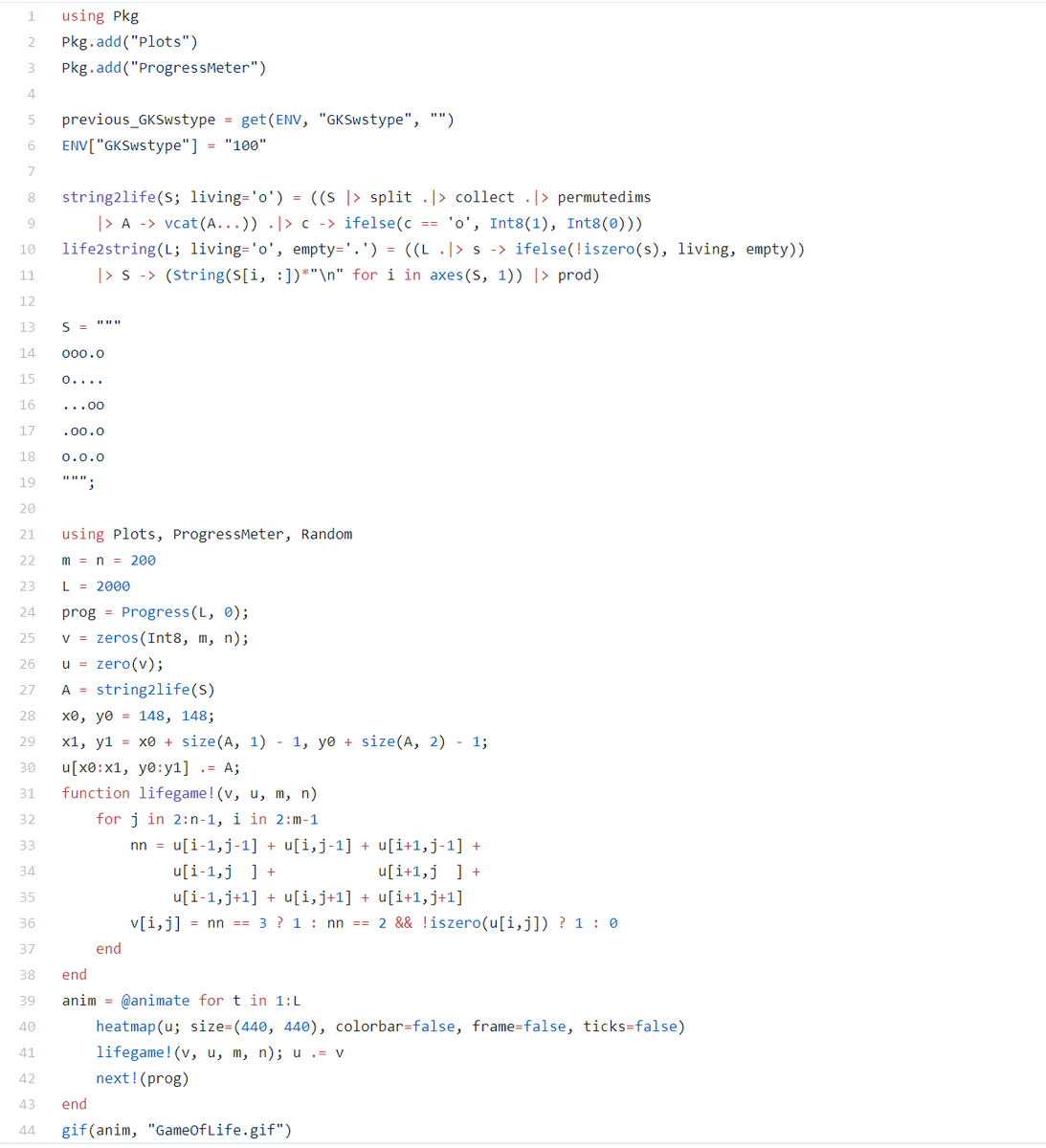
添付画像は10行ライフゲームのコード
初期条件やプログレスメーターやJuliaの文法で必要なendも含めて10行!
可読性も悪くないはず。
10行シリーズ全ソースコード↓
nbviewer.jupyter.org/gist/genkuroki…
添付画像は10行ライフゲームのコード
初期条件やプログレスメーターやJuliaの文法で必要なendも含めて10行!
可読性も悪くないはず。

#Julia言語 配列uに保持した状態を更新するコードを
for t in T
u = update(u)
end
の形式で行うと無駄なメモリアロケーションの嵐になる。
for t in T
update!(u)
end
のようにuの内容を更新するように書かないと損をする。
以下のライフゲームのコードもそうなっています。
for t in T
u = update(u)
end
の形式で行うと無駄なメモリアロケーションの嵐になる。
for t in T
update!(u)
end
のようにuの内容を更新するように書かないと損をする。
以下のライフゲームのコードもそうなっています。

#Julia言語 配列に保持した状態を時間発展させるコードはありがちなので、ライフゲームのような遊びのプログラム作成もバカにできない。10行の中に基本が詰まっている。
10行の中にプログレスメーターを入れる余裕があるとちょっとうれしい。
10行の中にプログレスメーターを入れる余裕があるとちょっとうれしい。

#Julia言語 逆温度βはサイズ→∞のときの理論的な相転移点直上の値にしてあります。
#Julia言語 10行シリーズ
1. 信頼区間が二項分布モデルのパラメータ値を含む確率
2. 同ケースでの信頼区間の分布
3. 以上のFisher検定版
4. 3次元ランダムウォーク
5. Ising2D.jl
6. 蔵本モデル
7. ジュリア集合
8. マンデルブロ集合
9. ライフゲーム
10. 2D Ising model
↓
nbviewer.jupyter.org/gist/genkuroki…
1. 信頼区間が二項分布モデルのパラメータ値を含む確率
2. 同ケースでの信頼区間の分布
3. 以上のFisher検定版
4. 3次元ランダムウォーク
5. Ising2D.jl
6. 蔵本モデル
7. ジュリア集合
8. マンデルブロ集合
9. ライフゲーム
10. 2D Ising model
↓
nbviewer.jupyter.org/gist/genkuroki…
#Julia言語 2D Ising modelのモンテカルロシミュレーションの動画を10行で作っているのって、結構すごくね?
可読性はそう悪くないし、最後の10行目はforループの終わりのendだけで、プログレスメーターまで付いている。ising2d!函数では計算速度も犠牲にしていない。
nbviewer.jupyter.org/gist/genkuroki…
可読性はそう悪くないし、最後の10行目はforループの終わりのendだけで、プログレスメーターまで付いている。ising2d!函数では計算速度も犠牲にしていない。
nbviewer.jupyter.org/gist/genkuroki…

#Julia言語 の公式バイナリは
julialang.org/downloads/
からダウンロード可能。Jupyterとの連携については
nbviewer.jupyter.org/github/genkuro…
が詳しい。
julialang.org/downloads/
からダウンロード可能。Jupyterとの連携については
nbviewer.jupyter.org/github/genkuro…
が詳しい。
#Julia言語 Jupyterとの連携が取れなくても
gist.github.com/genkuroki/9937…
のコードを julia 公式バイナリを実行して出て来たREPLに貼り付ければ2次元Isingモデルの動画を作れます。
すでに Plots.jl と ProgressMeter.jl のインストールが終わっている人は5行目以降を貼り付ける。
gist.github.com/genkuroki/9937…
のコードを julia 公式バイナリを実行して出て来たREPLに貼り付ければ2次元Isingモデルの動画を作れます。
すでに Plots.jl と ProgressMeter.jl のインストールが終わっている人は5行目以降を貼り付ける。

#Julia言語 Jupyerとの連携が取れない人であっても、ライフゲームで遊べるようなコードも公開しました。
gist.github.com/genkuroki/9e2b…
使い方は1つ前のツイートと同じ。REPLに貼り付ける。(julia GemeOfLife.jl でもよいです。)
S の定義や x0, y0 の定義などを変えれば、初期条件を変更できます。
gist.github.com/genkuroki/9e2b…
使い方は1つ前のツイートと同じ。REPLに貼り付ける。(julia GemeOfLife.jl でもよいです。)
S の定義や x0, y0 の定義などを変えれば、初期条件を変更できます。
#Julia言語 2d_Ising.jl と同じ方法を GameOfLife.jl でも使うようにすれば GameOfLife.jl 側も周期境界条件にできます。(もちろん、もっと別の境界条件も可能。)
• • •
Missing some Tweet in this thread? You can try to
force a refresh