Thread by @arnaugamez

Ok, I had some time to read the new paper on MBA deobfuscation: usenix.org/conference/use…

TL;DR Cool stuff and great contribution, but tarnished by some omissions that make it seem to have a bigger impact and general applicability than it really has, imho.

A thread 🧵

First things first. I don't consider myself an expert, but I'm quite familiar with academic literature regarding MBA (de)obfuscation. This paper constitutes great research, provides a novel proof and offers promising results.

That being said, I think it is necessary to point out some omissions, limitations and/or formal inaccuracies that might not be obvious if one is not familiar with MBA literature. I'll use excerpts from my thesis (

https://twitter.com/arnaugamez/status/1286676744607604744?s=20

) and literature to clarify some ideas.

The definition that the paper provides for an MBA expression is what literature defines as a linear MBA expressions, excluding the more general definition usually referred to as polynomial MBA expression.

Thus, from the very beginning we must know that the paper will deal with a subset of MBA expressions, and this fact is not mentioned anywhere*.

*it can be vaguely deduced from a sentence at the very end of the paper, which we will see later.

Next, it appears that it is only addressing obfuscated MBA expressions that have been constructed through MBA rewriting rules, but not through insertion of (usually affine) identities.

It is not entirely clear to me that their deobfuscation method would apply directly to obfuscated expressions that involve some insertion of (affine) identities, but there are two indicators that this won't be the case or, at least, does not appear it has been tested.

First, the fact that when addressing Tigress obfuscation in 7.4, the EncodeData method is not included in the testbed (while it is used both in Syntia and QSynth testbeds afaik).

Second, this vague mention at the end of Discussion section: "It is also possible that attackers combine MBA obfuscation with other data encoding techniques to create complex expressions with bitwise and arithmetic operations but does not meet the MBA definition in this paper"

But what are MBA expressions if not "expressions with bitwise and arithmetic operations"?
Essentially, it is saying that what has been defined as an MBA expression is indeed a restricted subset, and that some MBA obfuscation transformations would not be covered by their approach.

Let's get to the core contribution of the paper: a way to reduce n-bit expressions to 1-bit expressions. This is an application that comes from proving the converse part of a known theorem (see section 2.2.3 from my thesis for a more detailed version and proof of sufficiency).

Essentially this theorem that allows us to derive linear MBA rewriting rules on N-bits starting from a {0,1}-matrix. By proving the converse part of the theorem, the authors of the paper prove that we can actually go the other way: form n-bit to 1-bit expressions (and back).

And this is really cool. But, based on this, they state that "The two-way feature in current MBA obfuscation implies that any n-bit obfuscated MBA expression can be simplified in 1-bit space. Consequently, the MBA reduction in 1-bit space is equivalent to that in n-bit space".

However, this affirmation is not correct, or at least not entirely precise imho, even restricting our analysis to linear MBA expressions: the underlying theorem provides the mechanism to work around "some" linear MBA expressions, but not necessarily all of them.

Indeed, Eyrolle's thesis already points out that for the theorem to hold, the bitwise operations cannot contain constants other than 0 and -1.

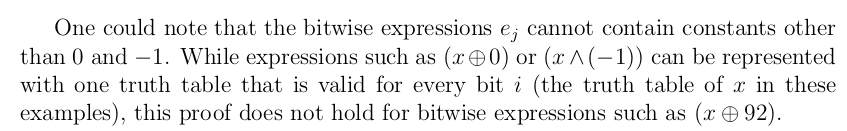
While not explained further, the reasoning behind it is pretty simple: the only way to map an n-bit constant to a 1-bit constant in a two-way manner is if the n-bit constant is either all zeroes (0) or all ones (-1).

Another thing that surprised me is no reference at all to QSynth paper from @quarkslab folks, which already introduced a kind of offline truth-table approach, in that case for a synthesis-based approach.

Moreover, the paper mentions that "The common limitation of existing deobfuscation efforts is that they treat MBA obfuscation as a black box, rather than investigate the mechanism under the hood".

Which is mostly true, except that QSynth paper already presented an algorithm for sub-AST (sub-expression) reasoning and simplification. Ok, QSynth implementation hasn't been made public afaik, but still.

Finally, a brief comment on the evaluation and results. So, why does it work so well? The first dataset seems to include basic "bit hacks" and MBA expressions from Eyrolles' thesis appendices, which are essentially rewriting rules derived using the aforementioned theorem.

The second dataset appears to be constructed by the authors using the rewriting rules approach that they described, which constitutes the MBA obfuscation approach addressed from a deobfuscation point of view in the paper.

(Take this with a grain of salt for the moment. Waiting for the datasets to be published, but that's my understanding from what is mentioned in the paper).

For the more real-world examples, my guess (and my general observation in the wild) is that *everyone* is using the *same* kind of (linear) MBA rewriting rules for MBA obfuscation because these are the ones easily available publicly and known to be easy to generate.

Don't get me wrong, I'm not trying to undervalue their research achievements, real-world applicability and performance, which is undeniable, but to provide a greater context and background so we can all appreciate and position better the contributions made.

To sum up: great research and promising practical approach to deobfuscate a (large, and even "mainstream") subset of linear MBA expressions. I missed a better / more complete contextualization and clear applicability scope delimitation.