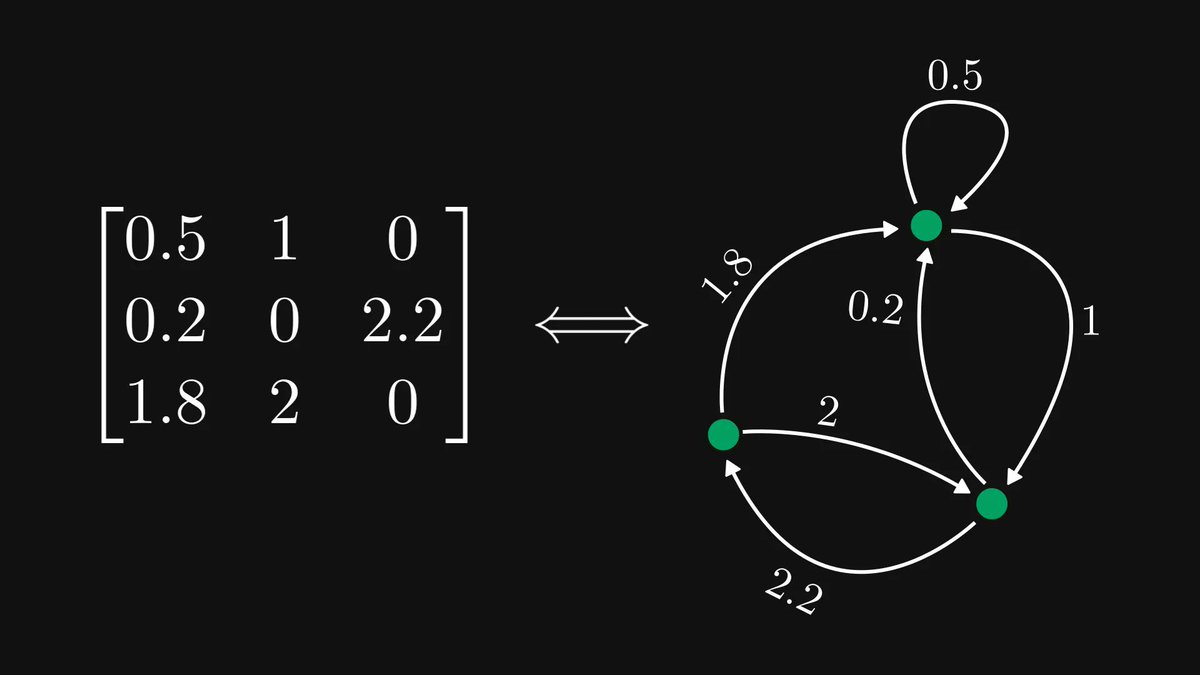
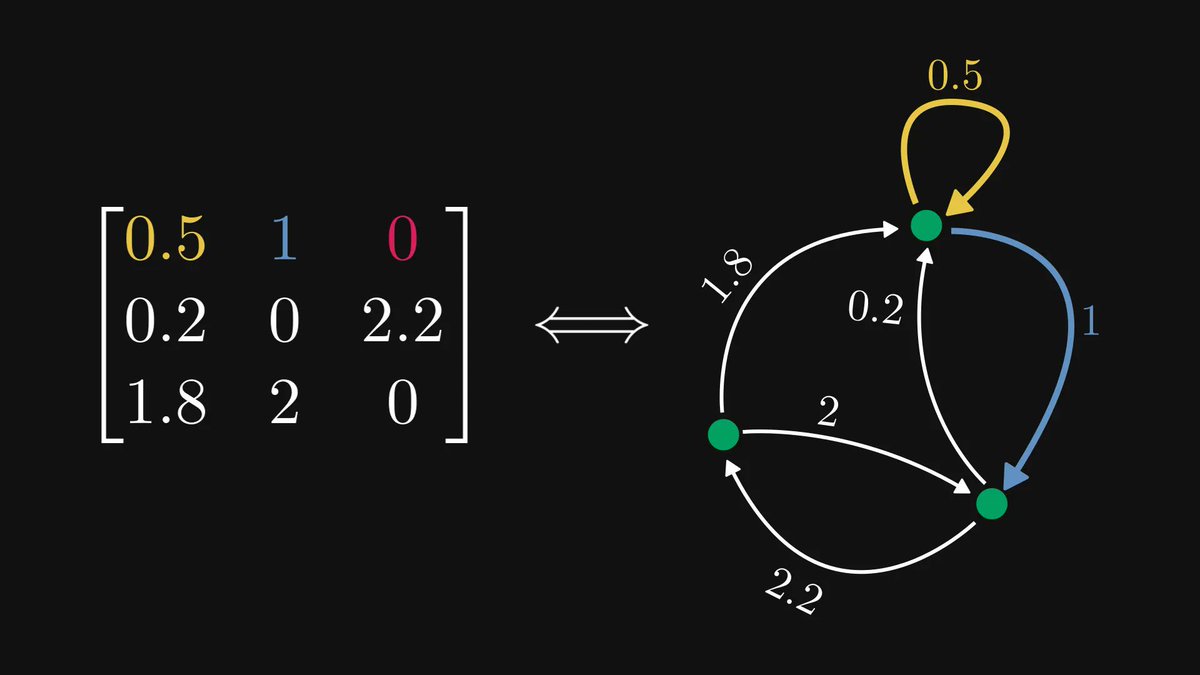
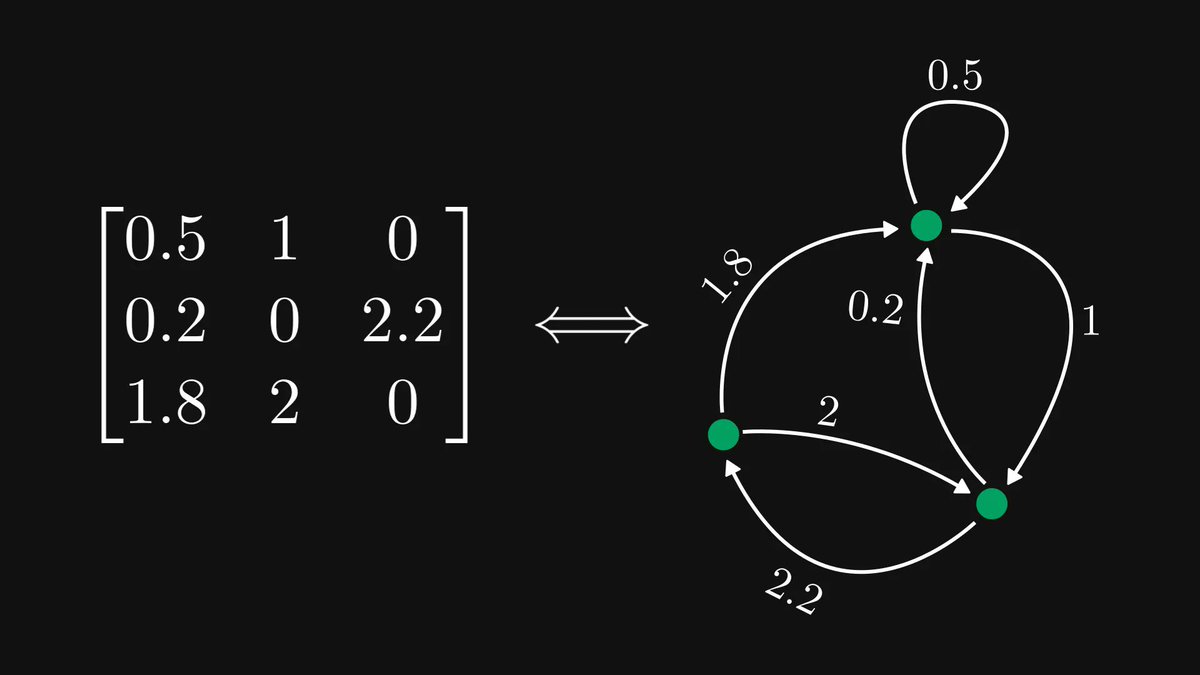
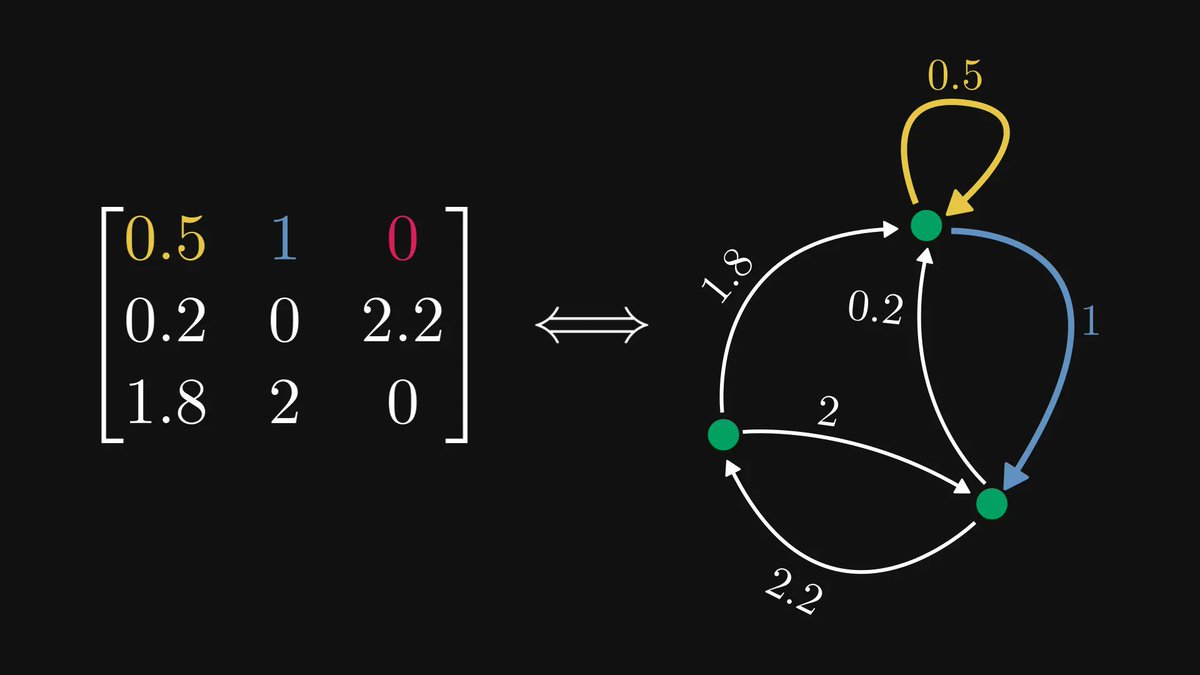
Have you ever wondered why include the logarithm in the definition of log-likelihood?
The answer is simple: logarithm makes differentiation of products easier.
Let's see why!
🧵 👇🏽
The answer is simple: logarithm makes differentiation of products easier.
Let's see why!
🧵 👇🏽
Although the derivative of a sum is the sum of derivatives, a similar property cannot be stated about the product of functions.
The derivative of a product is slightly more complicated: it is a sum of products.
The derivative of a product is slightly more complicated: it is a sum of products.
The formula gets even more complicated when we have more functions in the product.
When potentially hundreds of terms are present, like in the likelihood function, computing this is not feasible.
When potentially hundreds of terms are present, like in the likelihood function, computing this is not feasible.
This is where taking the logarithm can help us: it turns multiplication into addition!
So, instead of differentiating a product of 𝑛 functions, we have to deal with the sum!
Since the logarithm strictly increasing, it won't interfere with optimization either: the optimums are attained at the same place.
Since the logarithm strictly increasing, it won't interfere with optimization either: the optimums are attained at the same place.
If you enjoyed this explanation, consider following me and hitting a like/retweet on the first tweet of the thread!
I regularly post simple explanations of seemingly complicated concepts in machine learning, make sure you don't miss out on the next one!
I regularly post simple explanations of seemingly complicated concepts in machine learning, make sure you don't miss out on the next one!
https://twitter.com/TivadarDanka/status/1387032036402245633
• • •
Missing some Tweet in this thread? You can try to
force a refresh
