
I make math and machine learning accessible to everyone. Mathematician with an INTJ personality. Chaotic good.
31 subscribers
How to get URL link on X (Twitter) App


 First, the story:
First, the story:
 If you looked at the example above, you probably figured out the rule.
If you looked at the example above, you probably figured out the rule.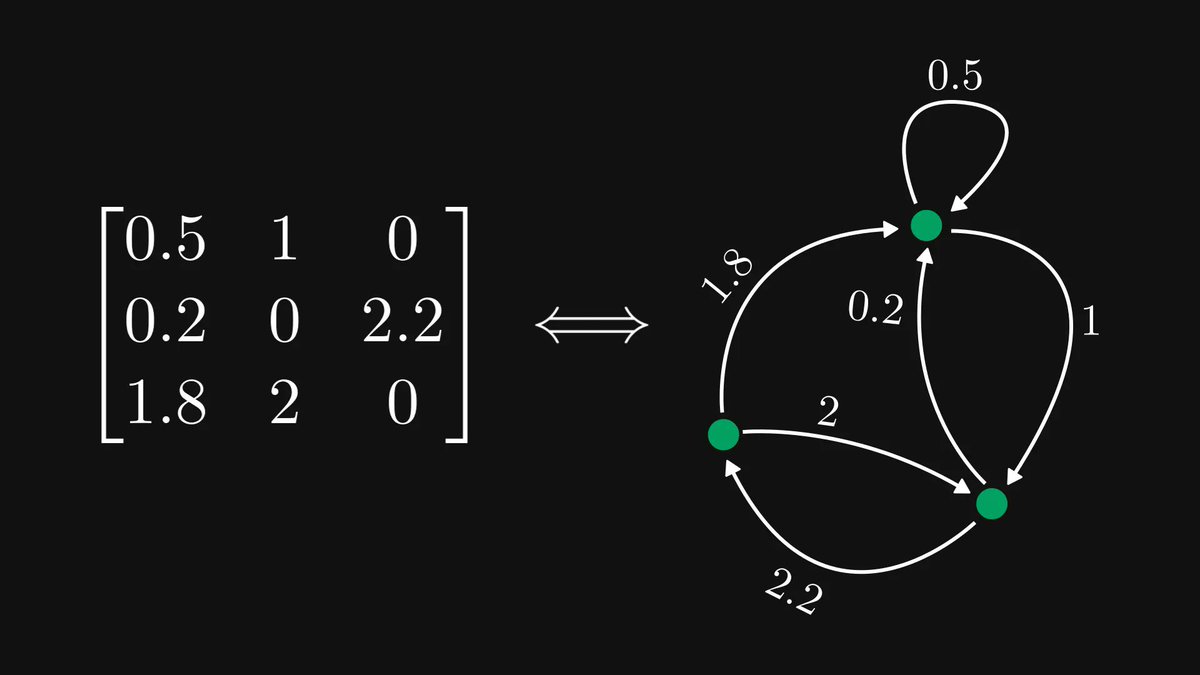
 If you looked at the example above, you probably figured out the rule.
If you looked at the example above, you probably figured out the rule.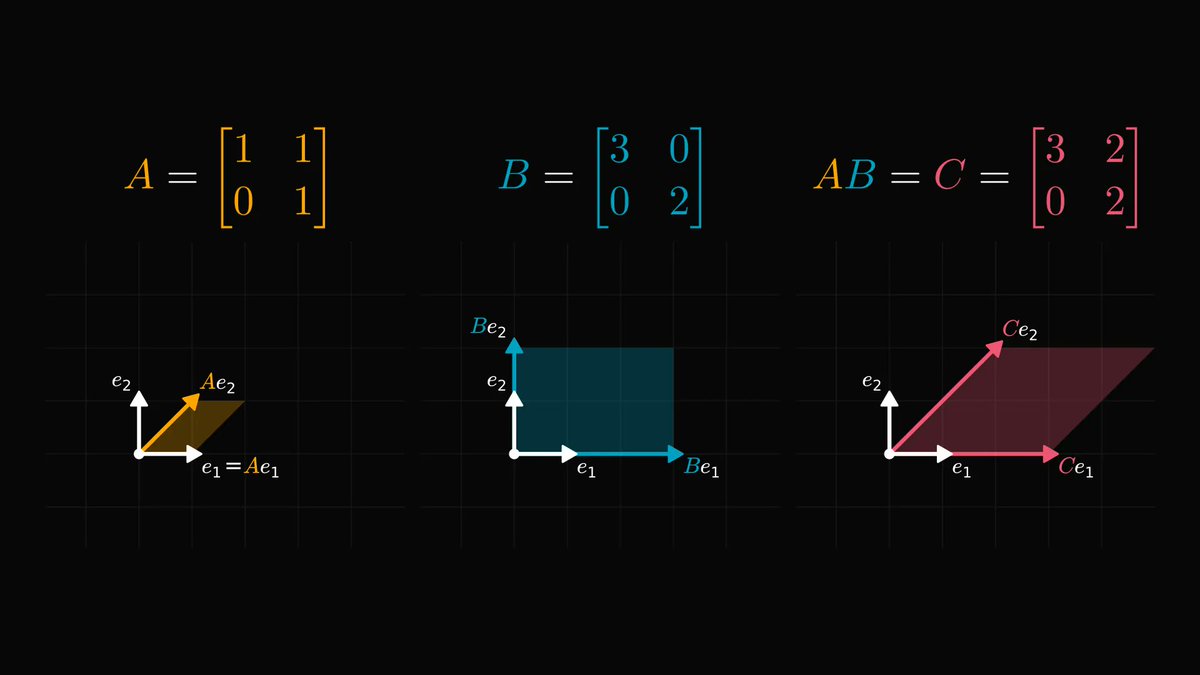
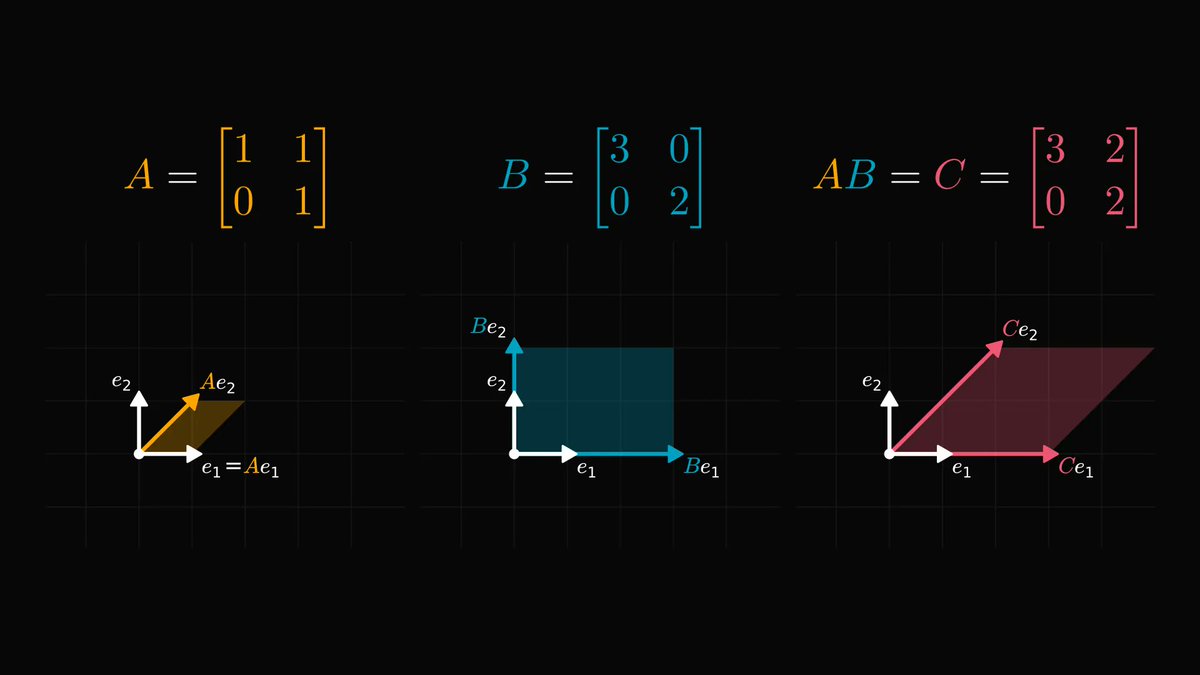 First, the raw definition.
First, the raw definition.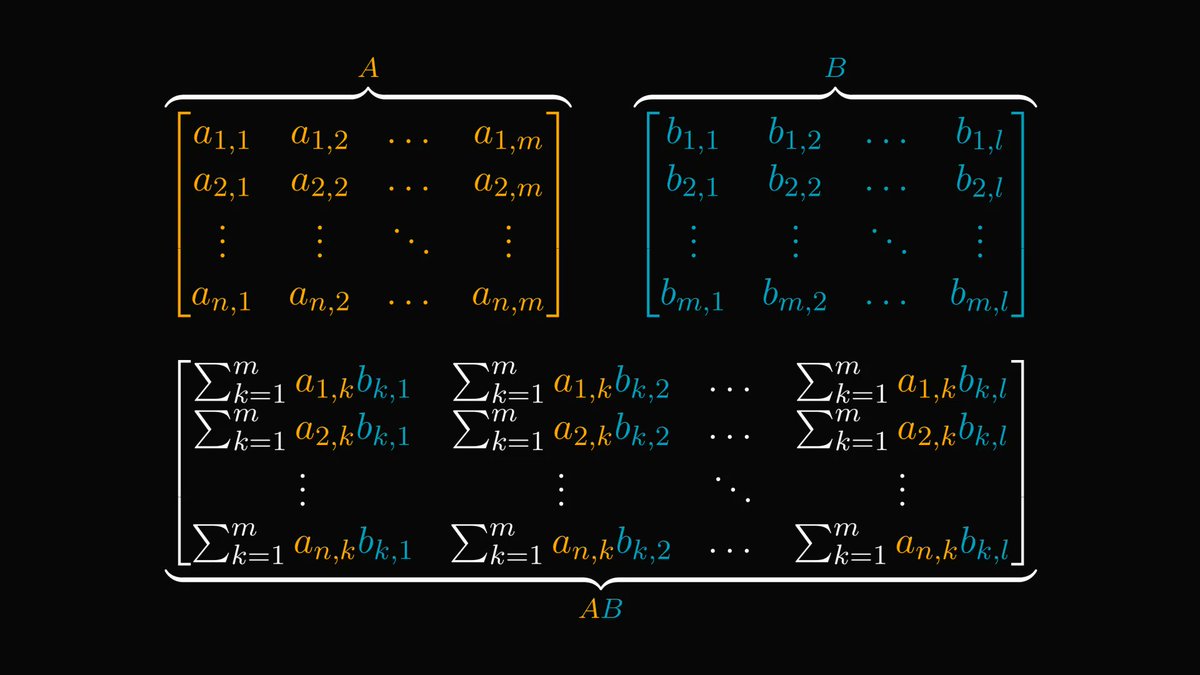

 First, let's look at what is probability.
First, let's look at what is probability.
 If you looked at the example above, you probably figured out the rule.
If you looked at the example above, you probably figured out the rule.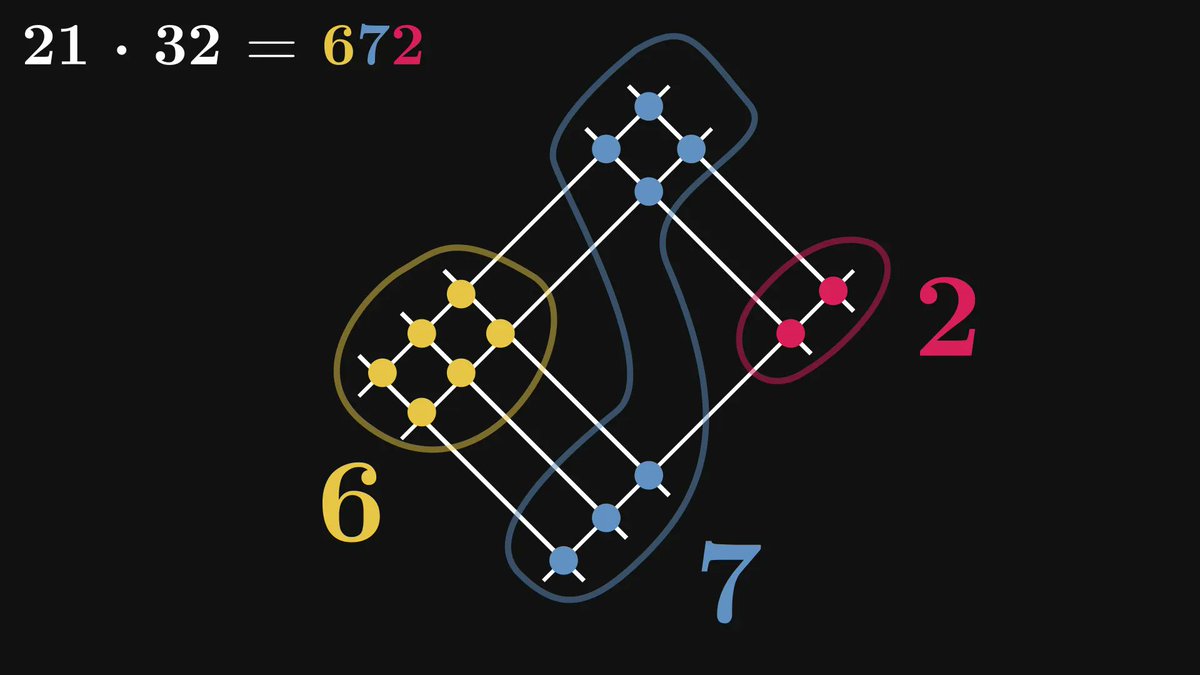
 First, the method.
First, the method.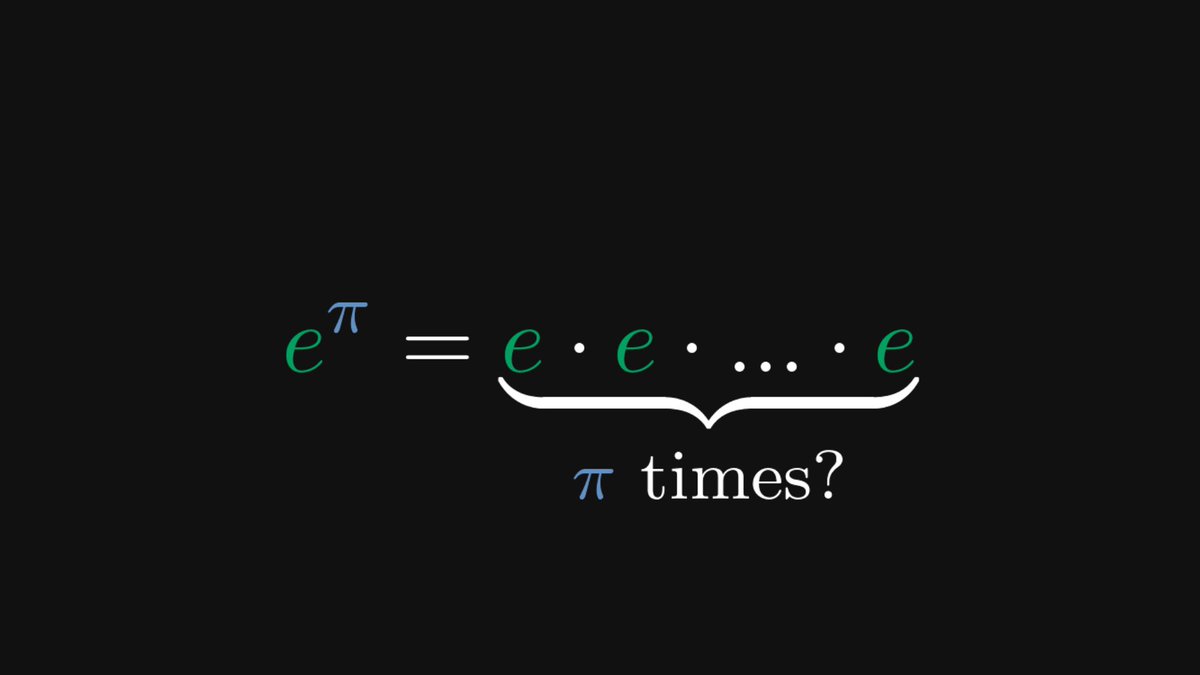
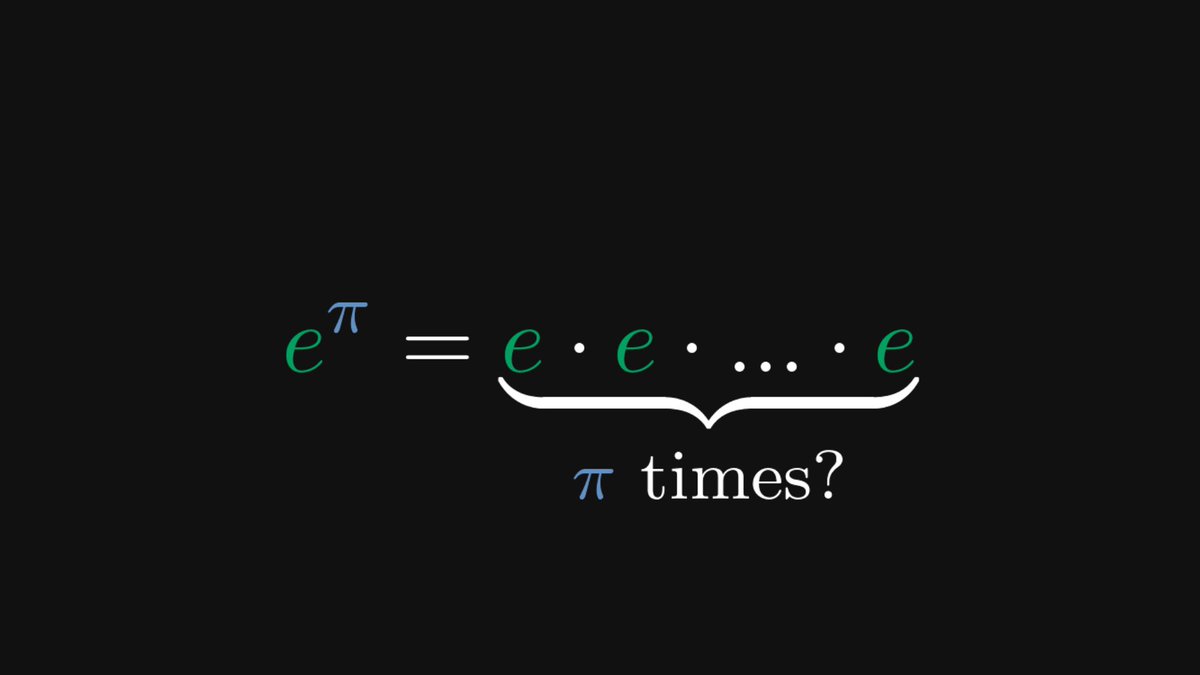 First things first: terminologies.
First things first: terminologies.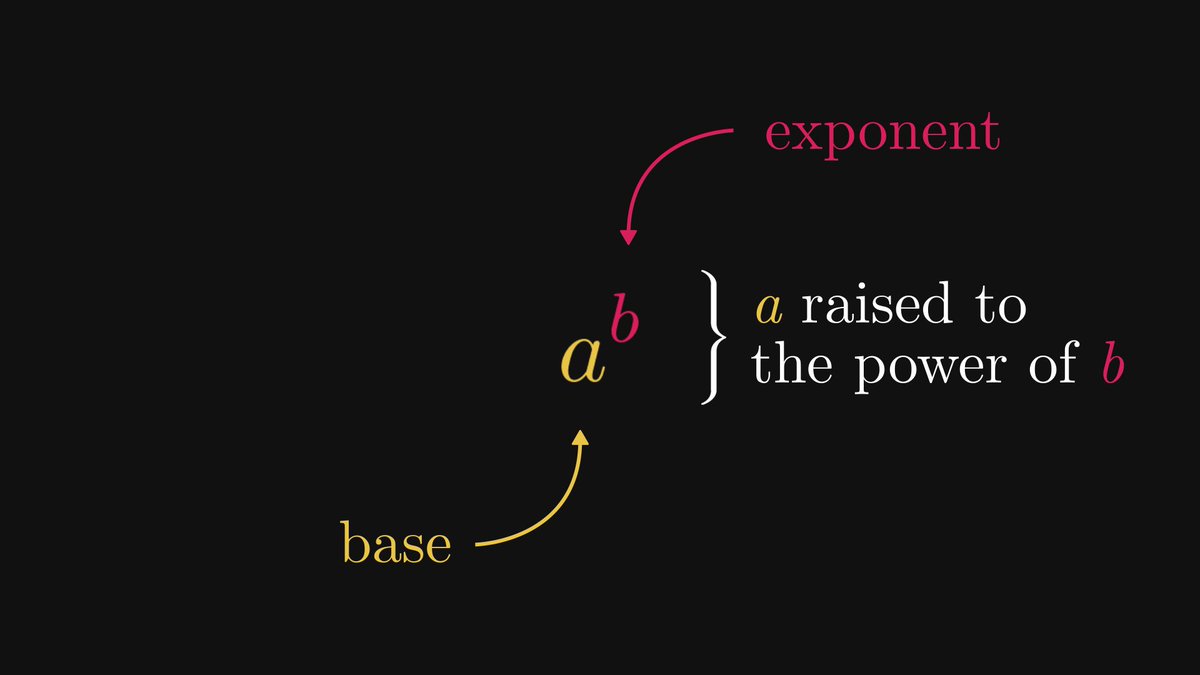
 In general, a function assigns elements of one set to another.
In general, a function assigns elements of one set to another.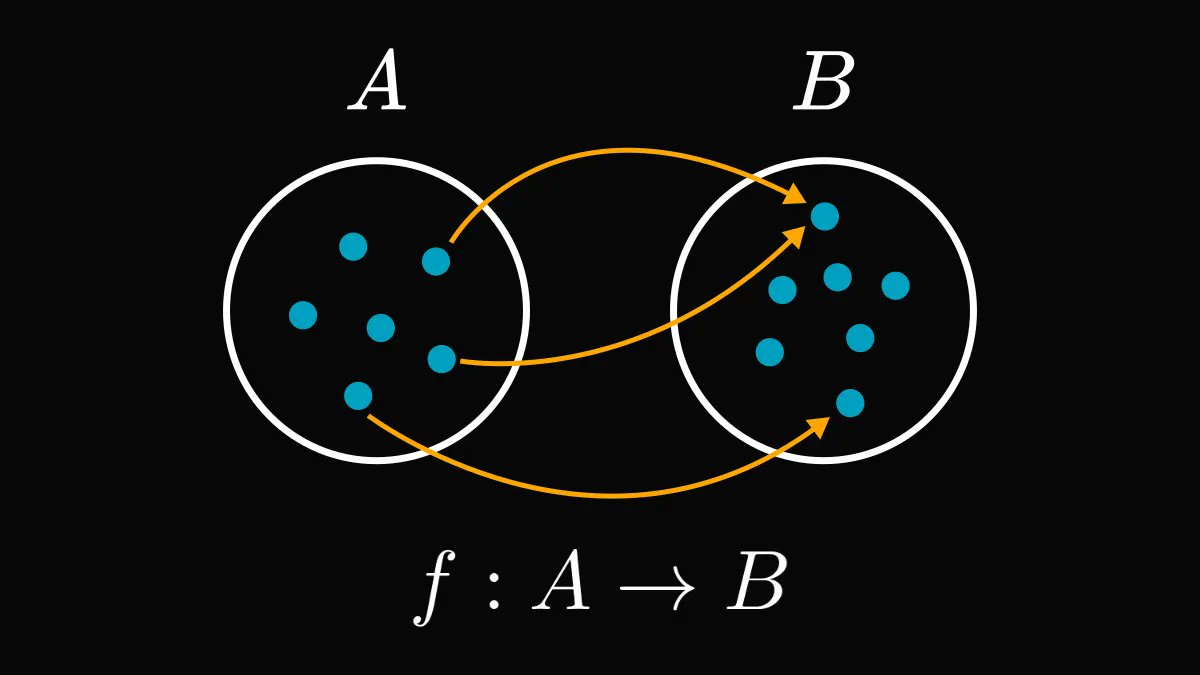
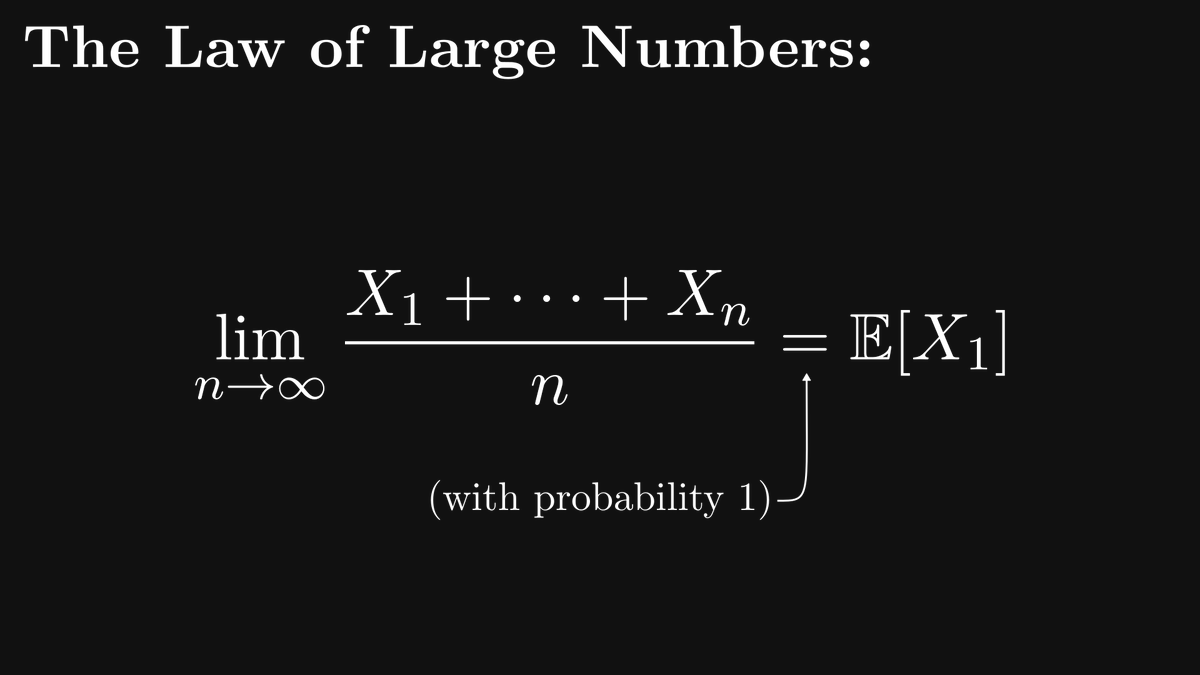
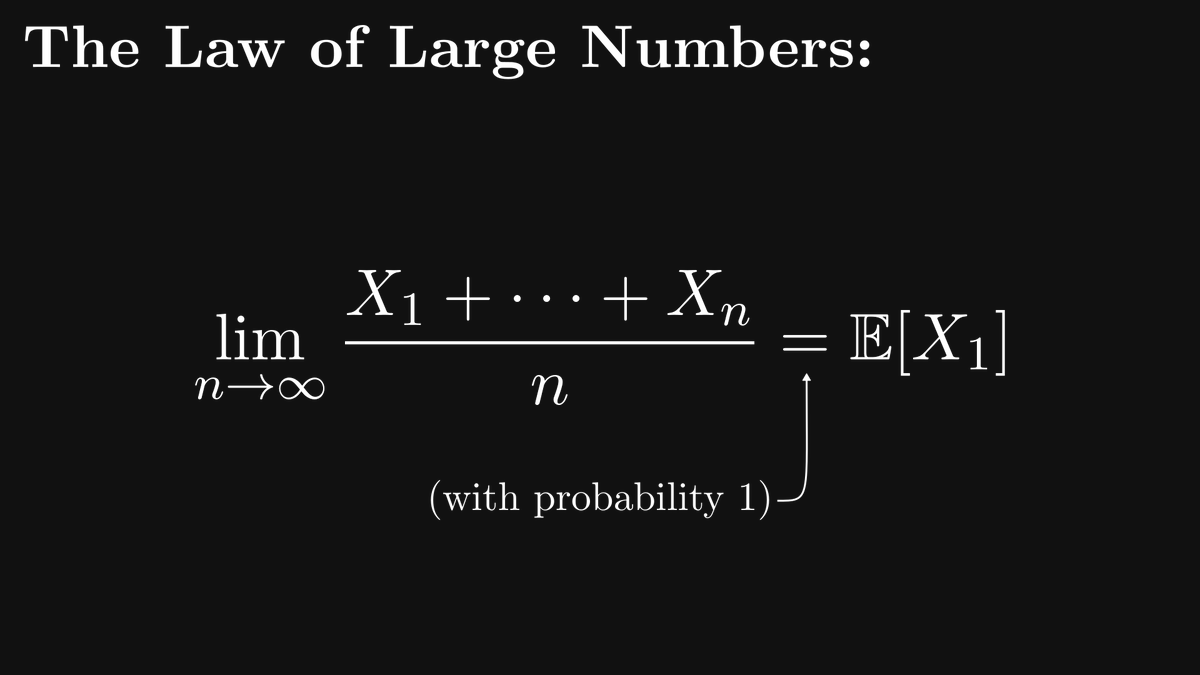 The strength of probability theory lies in its ability to translate complex random phenomena into coin tosses, dice rolls, and other simple experiments.
The strength of probability theory lies in its ability to translate complex random phenomena into coin tosses, dice rolls, and other simple experiments.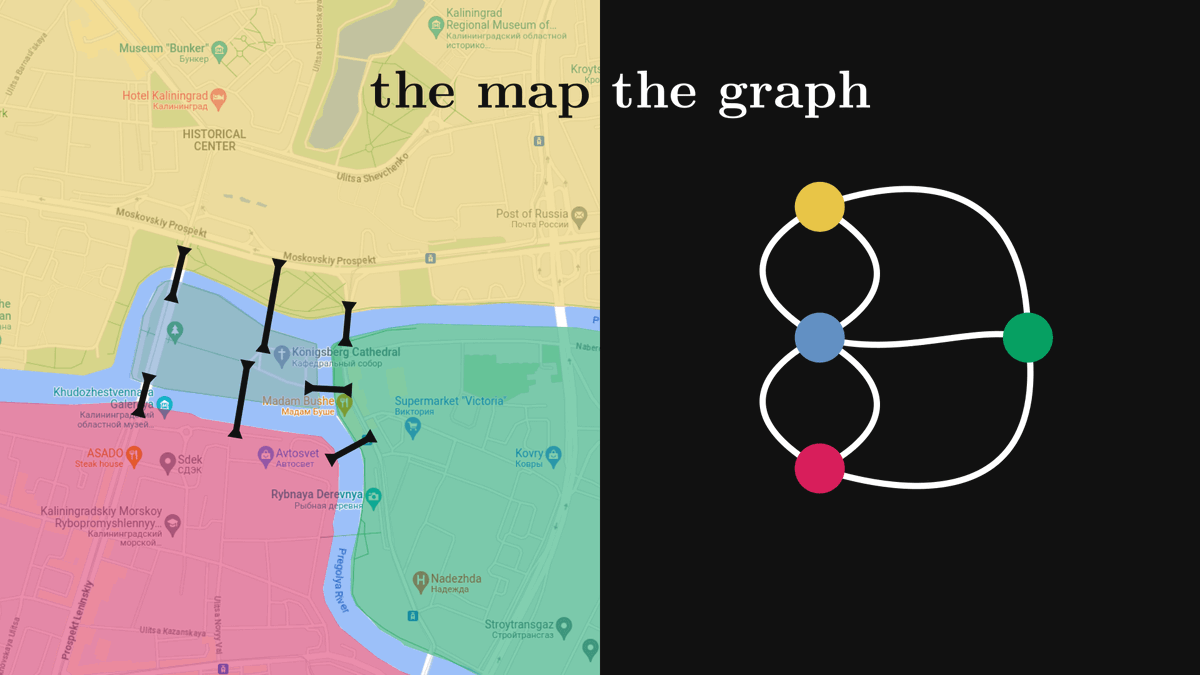
 Let's start with a story.
Let's start with a story.
 By definition, the dot product (or inner product) of two vectors is defined by the sum of coordinate products.
By definition, the dot product (or inner product) of two vectors is defined by the sum of coordinate products. 

 We are going to study three matrix factorizations:
We are going to study three matrix factorizations:
 First, the story:
First, the story:

 First, the raw definition.
First, the raw definition.

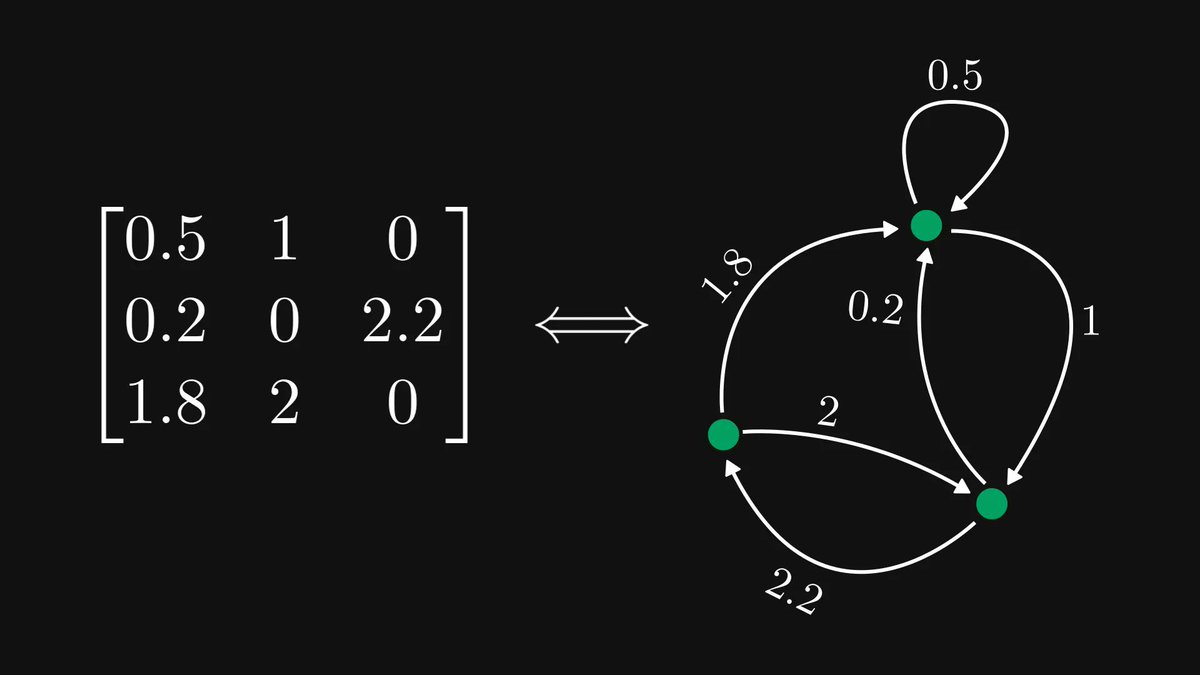
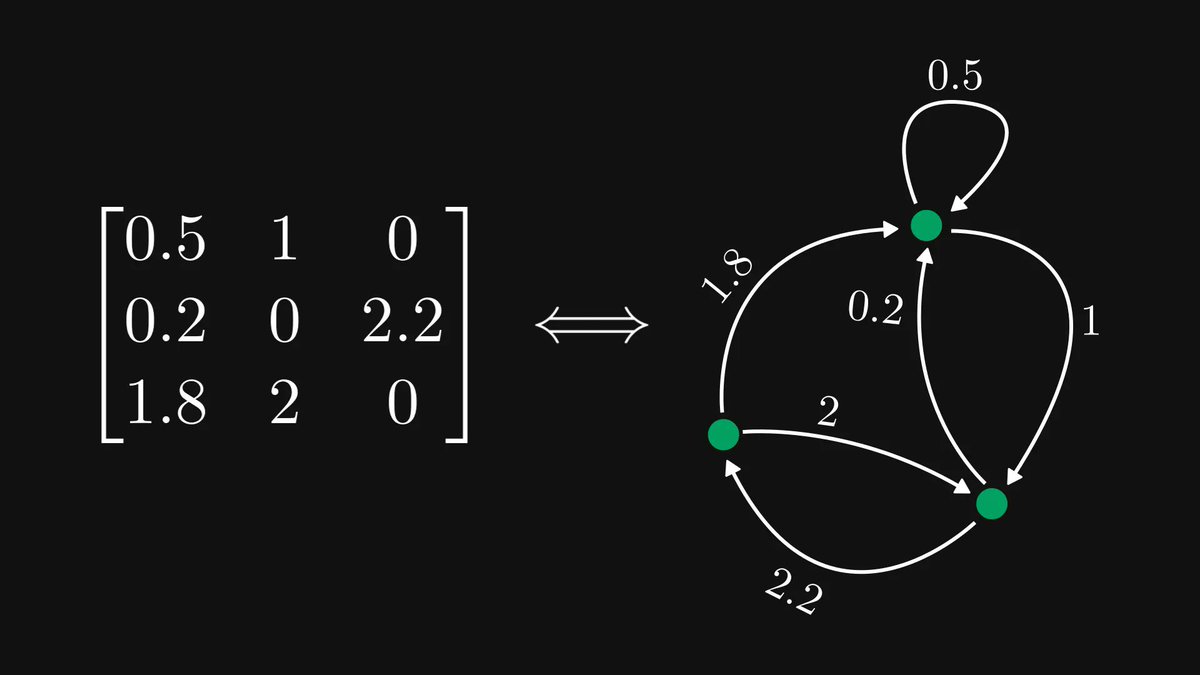
 What do the internet, your brain, the entire list of people you’ve ever met, and the city you live in have in common?
What do the internet, your brain, the entire list of people you’ve ever met, and the city you live in have in common?


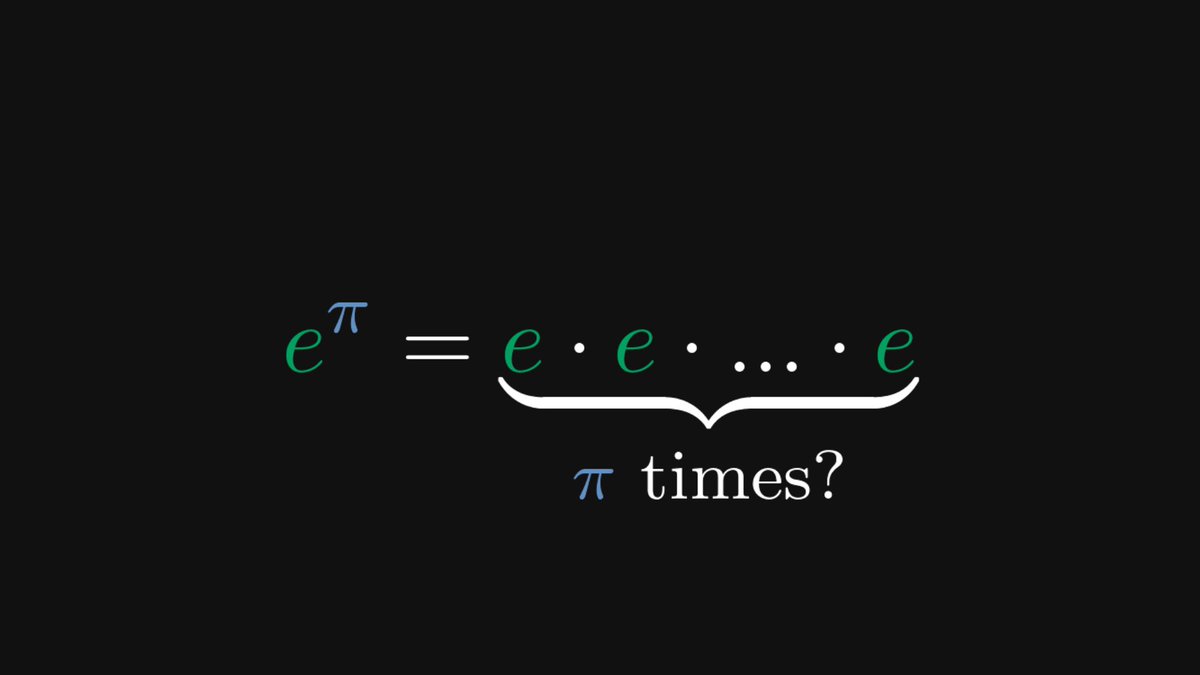
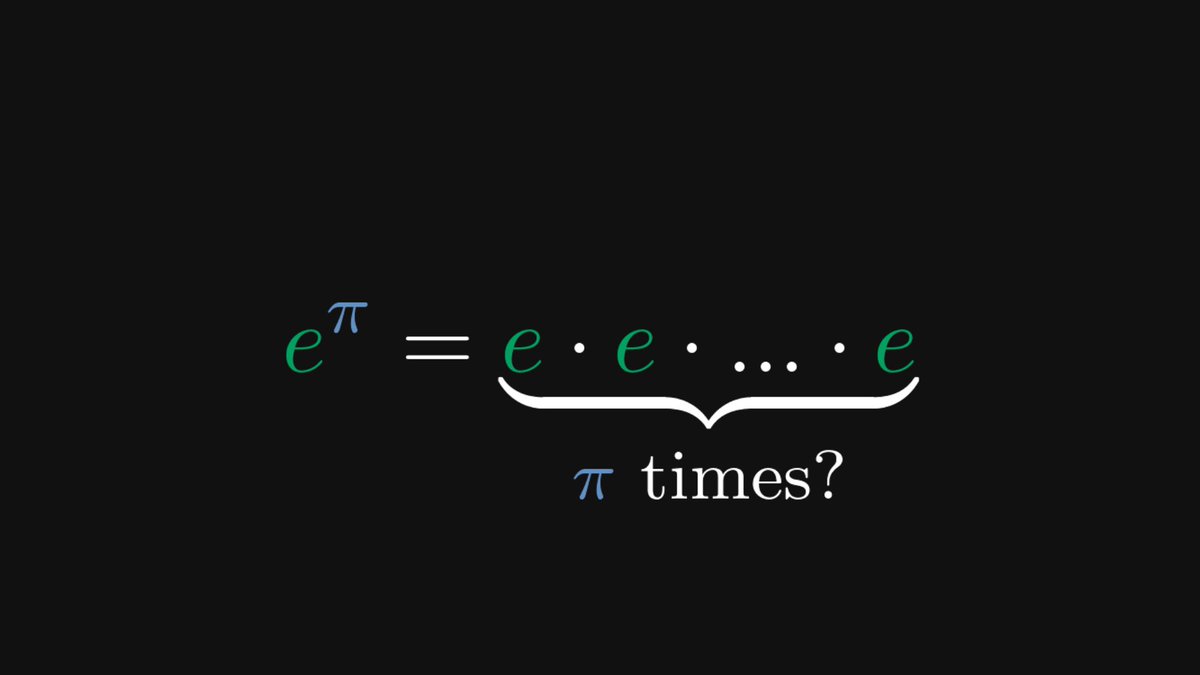 First things first: terminologies.
First things first: terminologies.

 In general, a function assigns elements of one set to another.
In general, a function assigns elements of one set to another.

 The strength of probability theory lies in its ability to translate complex random phenomena into coin tosses, dice rolls, and other simple experiments.
The strength of probability theory lies in its ability to translate complex random phenomena into coin tosses, dice rolls, and other simple experiments.
 Let's start with the basics: the inner product.
Let's start with the basics: the inner product.