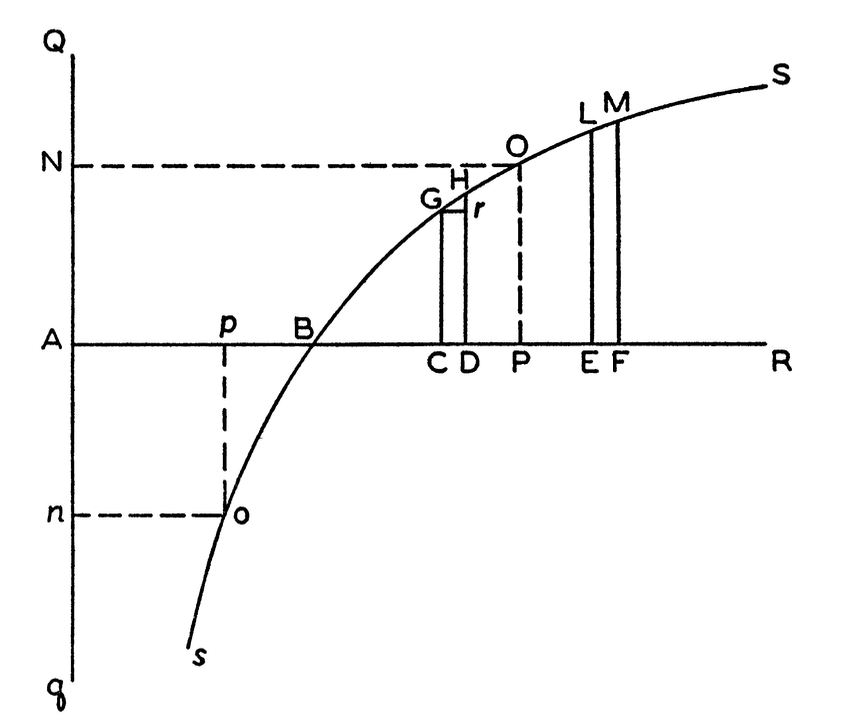
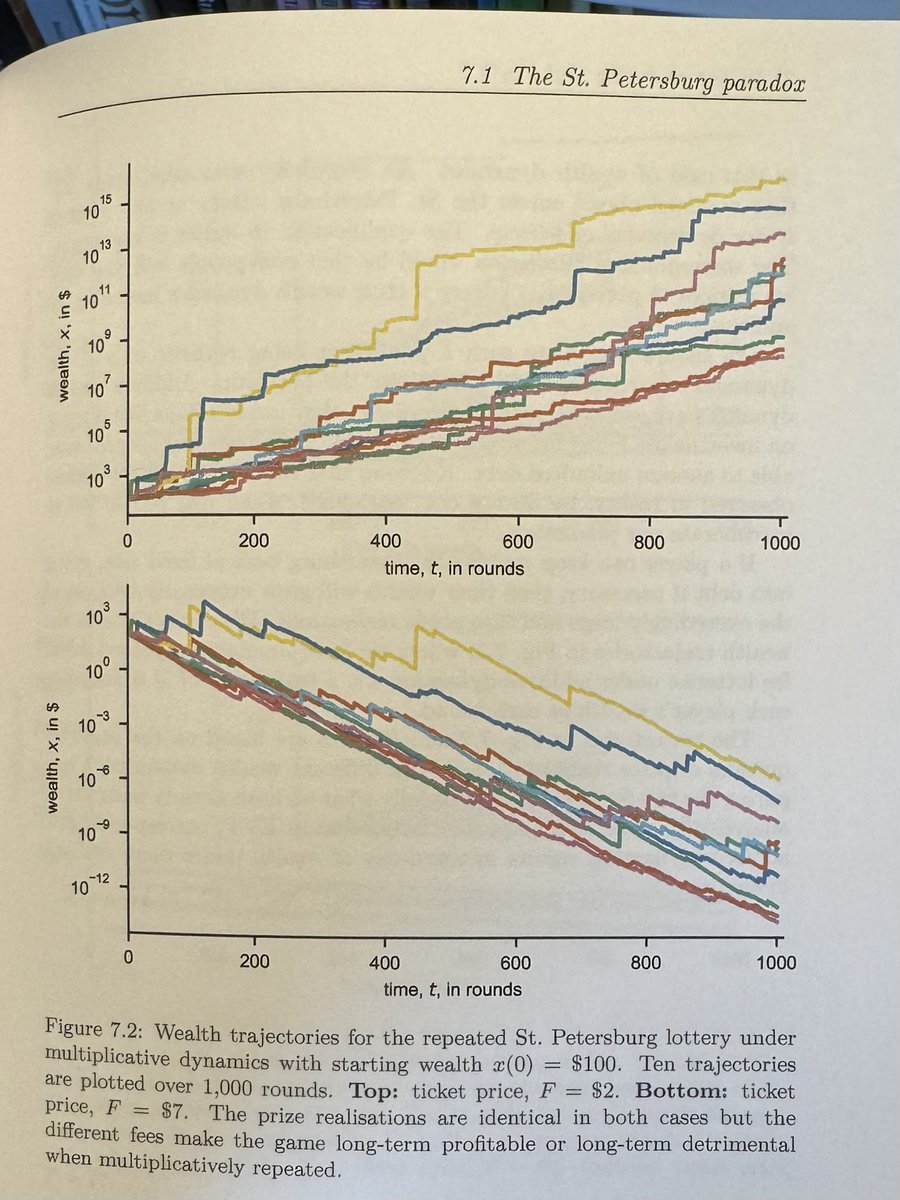
1/5
The Copenhagen experiment showed that Ergodicity Economics (EE), limited to its predicted utility functions for given dynamical settings, is a better fit to human behavior than classic expected-utility theory with a freely chosen single utility function.
The Copenhagen experiment showed that Ergodicity Economics (EE), limited to its predicted utility functions for given dynamical settings, is a better fit to human behavior than classic expected-utility theory with a freely chosen single utility function.

2/5
I don’t find this terribly interesting. Classic expected-utility theory is conceptually flawed, and science is more than data-fitting. However well or poorly it fits observations, one would have to reject expected-utility theory anyway.
I don’t find this terribly interesting. Classic expected-utility theory is conceptually flawed, and science is more than data-fitting. However well or poorly it fits observations, one would have to reject expected-utility theory anyway.
3/5
Here is what's interesting: I didn’t think EE would perform well in the Copenhagen experiment because I had bought into the narrative that the tested behavior was shaped by evolution over millions of years and cannot be re-learned on short time scales.
Here is what's interesting: I didn’t think EE would perform well in the Copenhagen experiment because I had bought into the narrative that the tested behavior was shaped by evolution over millions of years and cannot be re-learned on short time scales.
4/5
The experiment finds something else: we’re astonishingly quick at adapting to new dynamic environments. This opens the door to a whole new way of thinking about how and what we can learn. The brain is far more plastic than economic models suggest.
The experiment finds something else: we’re astonishingly quick at adapting to new dynamic environments. This opens the door to a whole new way of thinking about how and what we can learn. The brain is far more plastic than economic models suggest.

5/5
The really exciting bit: economic decision models are widely used in neuroscience. If we can improve on these models, it can have a direct effect on neuroscience.
Hence my enthusiasm for our collaboration with @DRCMR_MRI.
The really exciting bit: economic decision models are widely used in neuroscience. If we can improve on these models, it can have a direct effect on neuroscience.
Hence my enthusiasm for our collaboration with @DRCMR_MRI.
• • •
Missing some Tweet in this thread? You can try to
force a refresh