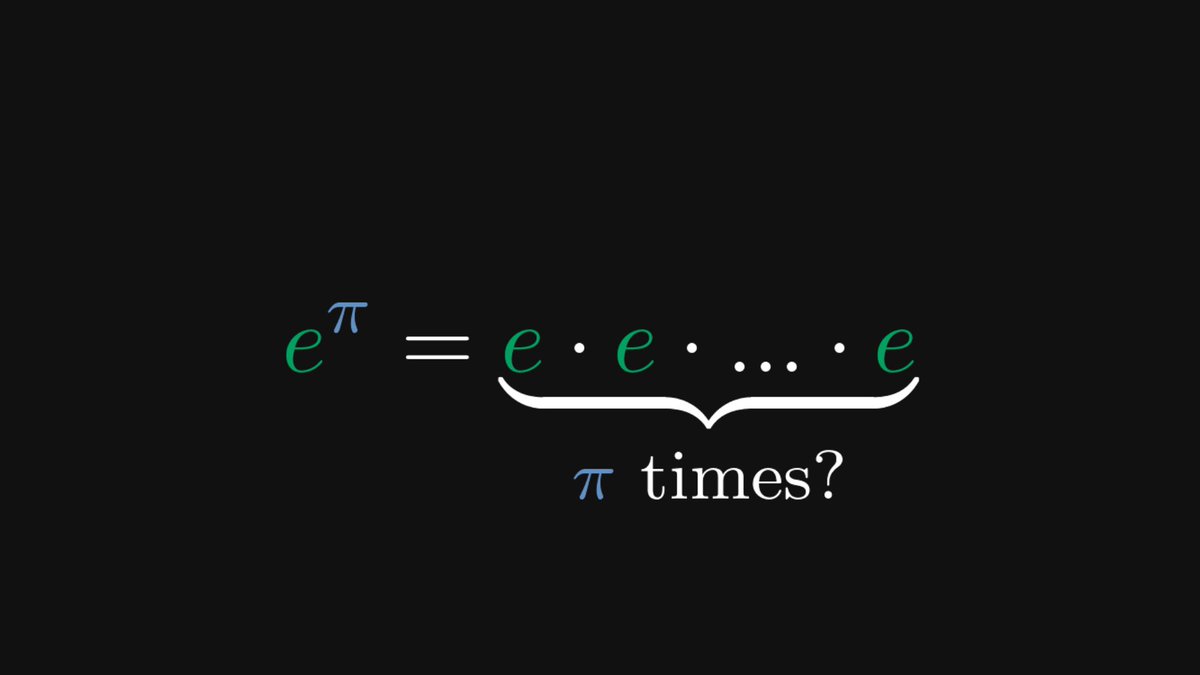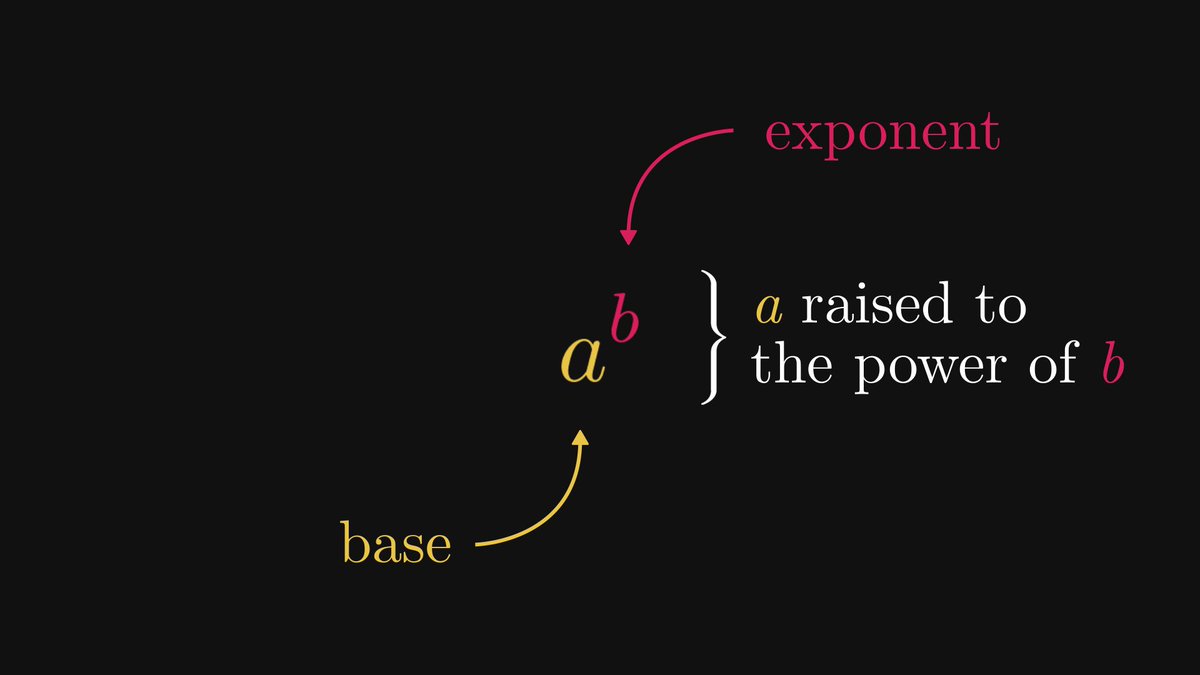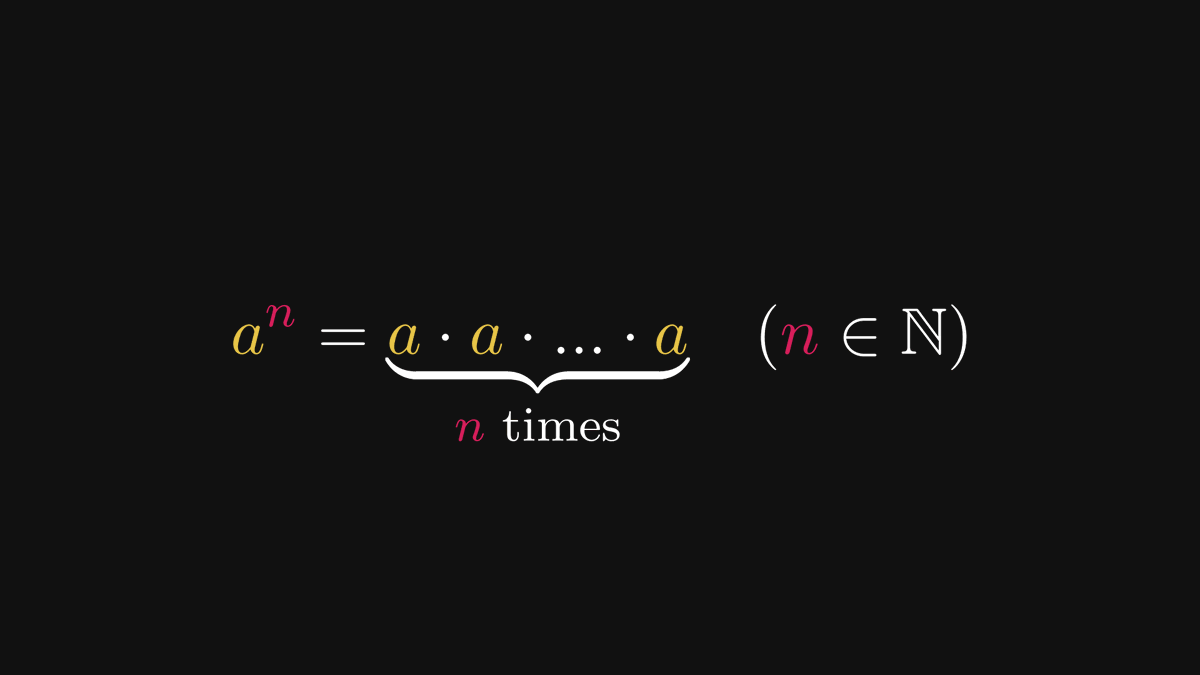There is a mathematical formula so beautiful that it is almost unbelievable.
Euler's identity combines the famous numbers 𝑒, 𝑖, π, 0, and 1 in a single constellation. At first sight, most people doubt that it is true. Surprisingly, it is.
This is why.
🧵 👇🏽
Euler's identity combines the famous numbers 𝑒, 𝑖, π, 0, and 1 in a single constellation. At first sight, most people doubt that it is true. Surprisingly, it is.
This is why.
🧵 👇🏽

Let's talk about the famous exponential function 𝑒ˣ first.
Have you ever thought about how is this calculated in practice? After all, raising an irrational number to any power is not trivial.
It turns out that the function can be written as an infinite sum!
Have you ever thought about how is this calculated in practice? After all, raising an irrational number to any power is not trivial.
It turns out that the function can be written as an infinite sum!

In fact, this can be done with many other functions.
For those that are differentiable infinitely many times, there is a recipe to find the infinite sum form. This form is called the Taylor expansion.
It does not always yield the original function, but it works for 𝑒ˣ.
For those that are differentiable infinitely many times, there is a recipe to find the infinite sum form. This form is called the Taylor expansion.
It does not always yield the original function, but it works for 𝑒ˣ.

Taylor expansions are advantageous for two reasons.
First, we can approximate functions by cutting of the sum at some N.
Second, we can simply extend functions to the complex plane with this formula!
First, we can approximate functions by cutting of the sum at some N.
Second, we can simply extend functions to the complex plane with this formula!

The exponential function is not the only one that can be written as a Taylor series.
We can also do this with the trigonometric functions sine and cosine.
(Feel free to check this by hand using the general Taylor expansion formula.)
We can also do this with the trigonometric functions sine and cosine.
(Feel free to check this by hand using the general Taylor expansion formula.)

By plugging in 𝑖𝑧 into the exponential function, we discover that the complex exponential function can be written in terms of trigonometric functions!
(We use that 𝑖² = -1.)
(We use that 𝑖² = -1.)

In the special case 𝑧 = π, we obtain the famous formula called Euler's identity.
This is how the magic happens.
This is how the magic happens.

When asked, Euler's identity often comes up among mathematicians as the most beautiful formula ever.
It is not only amazing because it connects together a bunch of famous constants, but because it establishes a connection between the exponential and trigonometric functions.
It is not only amazing because it connects together a bunch of famous constants, but because it establishes a connection between the exponential and trigonometric functions.
If you enjoyed this explanation, consider following me and hitting a like/retweet on the first tweet of the thread!
I regularly post simple explanations of mathematical concepts in machine learning, make sure you don't miss out on the next one!
I regularly post simple explanations of mathematical concepts in machine learning, make sure you don't miss out on the next one!
https://twitter.com/TivadarDanka/status/1392101188489916416
• • •
Missing some Tweet in this thread? You can try to
force a refresh