Thread by @HigherMathNotes

#MTBoS
What's your #calculus narrative? Do you have a one-sentence summary you can repeat to students throughout the course so that they absorb the main idea?

I was inspired by the attached thread to share my current best answer...

https://twitter.com/professorbrenda/status/1409572270339760131

My answer:

"Calculus makes hard problems easy with (1) approximations, (2) limits, and (3) shortcuts:

(1) approximate curvy shapes w/ straight shapes,
(2) find a limit by infinite refinement,
(3) apply general results to bypass limit calculation."

In tutoring, I call these the core principles of calculus. These get to the heart of the subject, but...

Q1: Shouldn't we mention the problems calculus tackles? Shouldn't we mention continuous change in some way?

Q2: Is the third principle on shortcuts really core to the subject?

Q3: How can we reinforce these principles?

Let's take these questions one at a time.

Q1: Shouldn't we mention the kinds of problems calculus tackles?

<A1>
Modeling continuous change should be a major emphasis. In particular, we should explain how problems about rates of change and accumulated change can be recast as geometric problems about slopes and areas.

However, characterizing calculus in terms of problems is bound to belie the enormity of its range.

If we want a single narrative, we can define calculus by its SOLUTIONS (principles (1)-(3)), not its PROBLEMS.
</A1>

Q2: Isn't calculus just about approximations & limits?

<A2>
Those arose in diverse cultures and were present in some form at least as far back as ancient Babylonia and Greece, but applications exploded after Newton and Leibniz developed systematic SHORTCUTS.

In the integral calculus, the FTC was basically known earlier. Newton and Leibniz "employed it to distill from the rich amalgam of earlier infinitesimal techniques a powerful algorithmic instrument for systematic calculation." [1]

The algorithms are the shortcuts.

In differential calculus, we can now also recognize a comprehensive algorithm for computing derivatives of standard functions, based on a system of shortcuts...

By working out the derivative as a limit for ATOMIC functions (powers, exponentials, trig functions, and their inverses), and MOLECULAR functions (sum, product, chain rule on two atoms), we have limit shortcuts for differentiating all matter in the standard universe.
</A2>

Q3. How can we reinforce these principles?

<A3>
One way to illustrate all three principles is by solving two problems from scratch on Day 1.

Ex 1. Determine slope of y=x^2 at x=3.
Ex 2. Determine area under y=x^2 from x=0 to x=3.

The order can be switched depending on taste.

Soln 1//
We only know one point on tangent line, but we need two for a slope. So, approximate by a secant.

Refining by moving 2nd point infinitely closer to x = 3 gives limit def. of dy/dx and a slope of 6.

If we do the same at x=a, we get the power rule as a general shortcut.

Soln 2//
Rectangles have the simplest area formula, so approximate with those to get Riemann sum.

Refining by increasing number of rectangles (assuming equal width) toward infinity gives limit def. of integral, and an area of 9.

The shortcut (the FTC) is based on the limit.

Note 1: If starting Calc 1 this way, it's best to avoid formal Riemann sums, but the area can be guessed with pictures or technology (if students can program, they could even write a numerical integrator). Allowing the FTC to be magic at this stage can inspire curiosity.

Note 2: Calc 2 could also be started with Ex. 1 on the slope of a parabola and Ex. 2 on the area under a parabola. In that case, these problems are a great way to review the main ideas of Calc 1, while also paving the way for applications...
</A3>

Q4: Here's a new question: I've focused on topics typically covered in Calc 1. What about Calc 2 and 3? Do the core principles unify the standard curriculum on applications of integration, on series, and on multivariable calculus?

<A4>
Yes, they do!

E.g. In Calc 2, to find the volume of a curvy shape, choose an approximating element (disk, shell...), refine the resulting approximation to get an integral, and use the FTC as a shortcut for a direct limit. This same approach can be illustrated in every example.

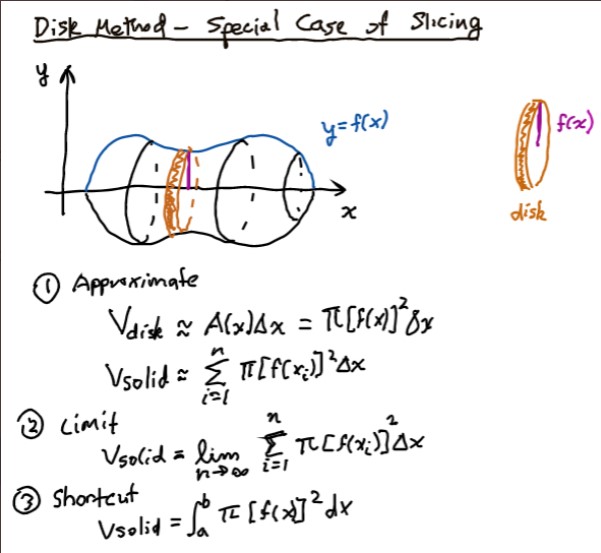
It's similar with series. Say we want a formula for sine.

(1) Can approximate by deg. 1 polynomial, but that's rigid. It can bend w/ deg. > 1.

(2) Infinite refinement leads to "infinite degree."

(3) Estimation theorems allow us to cut a series short while maintaining accuracy.

Note: Here, we aren't approximating nonlinear shapes by linear shapes in any obvious way, since for degree > 1 we have approximations that bend. So, this is a slight deviation from the details of core principle 1, but the general idea of approximation still applies.

In Calc 3, we have ample opportunity to reinforce the core principles.

E.g. How can we define the derivative and integral of a function of several variables? We can review how the principles led us to definitions for functions of a single variable, and then extend.
</A4>

CONCLUSION:
If we emphasize the core principles, students will get spaced, repeated exposure to the same ideas in a variety of new contexts.

After that, if you ask them what calculus is about, they'll have a good answer: it's about approximations, limits, and shortcuts.

Reference [1]:
The quote about how Newton and Leibniz contributed algorithms for systematic calculation is from *The Historical Development of the Calculus*, C.H. Edwards, Jr., 1979.

Reference [2]:
If you're interested to see calculus from the perspective of a math historian, check out the textbook by @viktorblasjo, which he generously offers for free from his website:

intellectualmathematics.com/calculus/

(Note: Any historical inaccuracies in this thread are my own!)

Reference [3]:

Infinity is a key aspect of principle (2) on limits. As the title suggests, Infinite Powers by @stevenstrogatz highlights a single "Infinity Principle" as the big idea, in much livelier prose than you see in this thread!

stevenstrogatz.com/books/infinite…

Reference [4]:
Above, I identified the atomic functions in a typical Calc 1 universe. For an approach that highlights the fundamental role of the exponential function and that does not shy away from special functions, see Calculus Green by @robertghrist:

youtube.com/playlist?list=…