Thread by @svlevine

Can we devise a more tractable RL problem if we give the agent examples of successful outcomes (states, not demos)? In MURAL, we show that uncertainty-aware classifiers trained with (meta) NML make RL much easier. At #ICML2021
arxiv.org/abs/2107.07184

A (short) thread:

The website has a summary: sites.google.com/view/mural-rl

If the agent gets some examples of high reward states, we can train a classifier to automatically provide shaped rewards (this is similar to methods like VICE). A standard classifier is not necessarily well shaped.

This is where the key idea in MURAL comes in: use normalized max likelihood (NML) to train a classifier that is aware of uncertainty. Label each state as either positive (success) or negative (failure), and use the ratio of likelihoods from these classifiers as reward!

This provides for exploration, since novel states will have higher uncertainty (hence reward closer to 50/50), while still shaping the reward to be larger closer to the example success states. This turns out to be a great way to do "directed" exploration.

Doing this tractably is hard, because we need two new classifiers for *every* state the agent visits, so to make this efficient, we use meta-learning (MAML) to meta-train one classifier to adapt to every label for every state very quickly, which we call meta-NML.

This ends up working very well across a wide range of manipulation, dexterous hand, and navigation tasks. To learn more about NML in deep learning, you can also check out Aurick Zhou's excellent blog post on this topic here: bairblog.github.io/2020/11/16/acn…

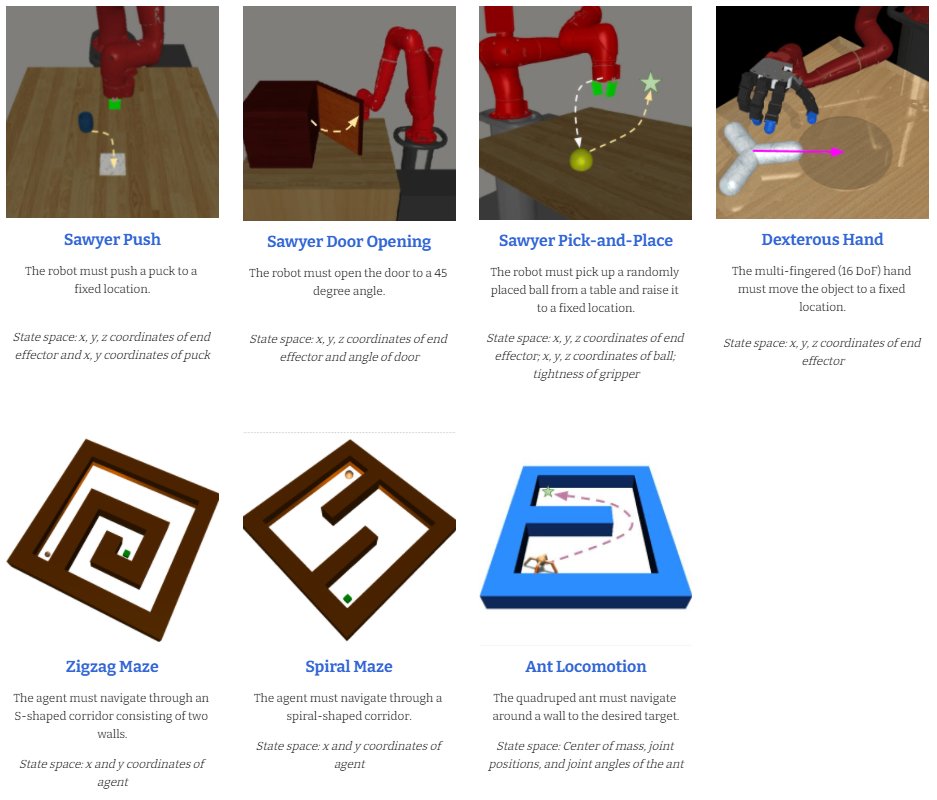
We'll present MURAL at #ICML2021.
Tue Jul 20 07:35 PM -- 07:40 PM (PDT): icml.cc/virtual/2021/s…

w/ Kevin Li, @abhishekunique, Ashwin Reddy, Vitchyr Pong, Aurick Zhou, Justin Yu