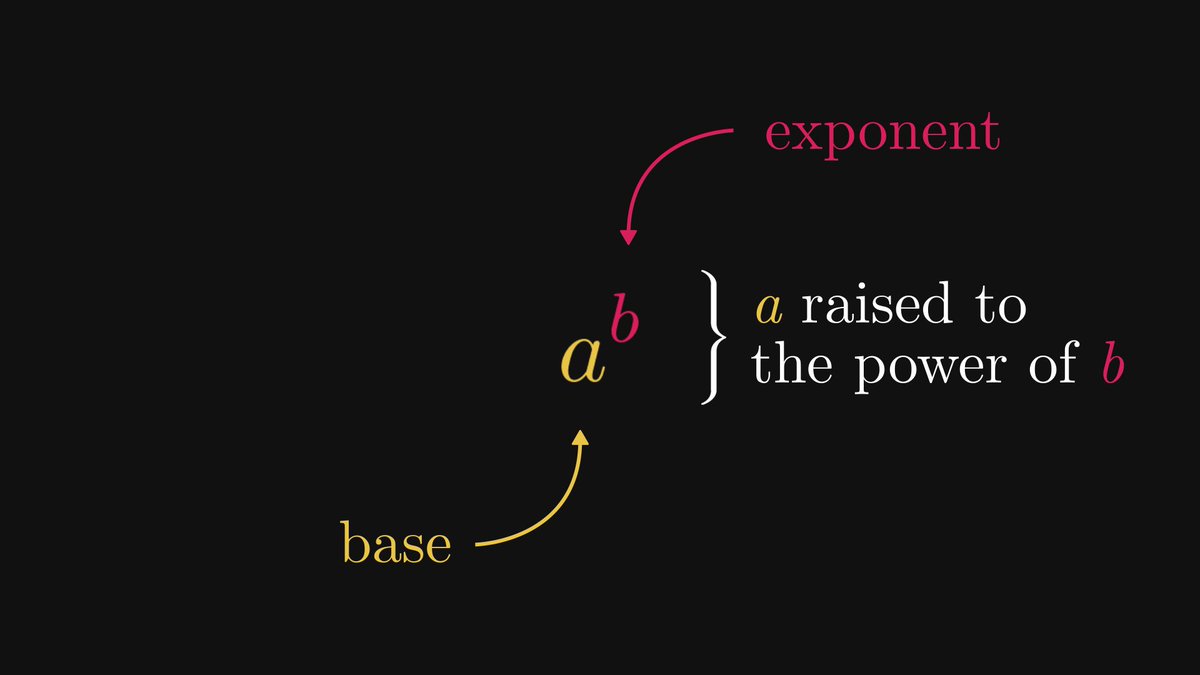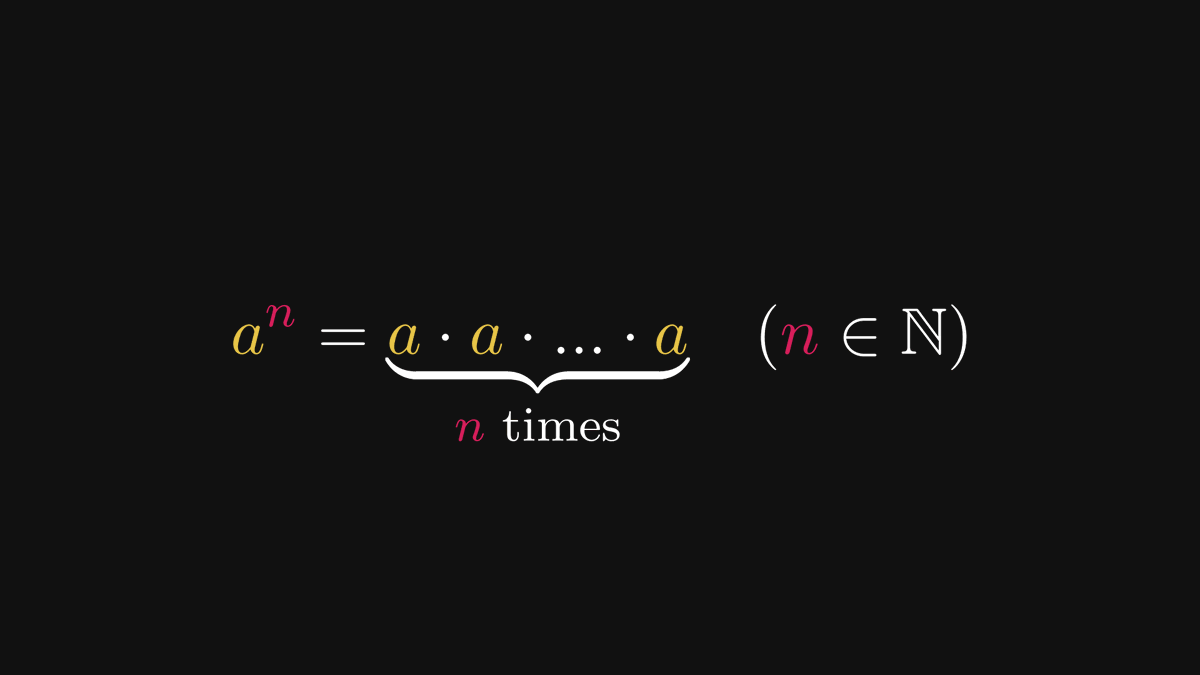There is one big reason we love the logarithm function in machine learning.
Logarithms help us reduce complexity by turning multiplication into addition. You might not know it, but they are behind a lot of things in machine learning.
Here is the entire story.
🧵 👇🏽
Logarithms help us reduce complexity by turning multiplication into addition. You might not know it, but they are behind a lot of things in machine learning.
Here is the entire story.
🧵 👇🏽

First, let's start with the definition of the logarithm.
The base 𝑎 logarithm of 𝑏 is simply the solution of the equation 𝑎ˣ = 𝑏.
Despite its simplicity, it has many useful properties that we take advantage of all the time.
The base 𝑎 logarithm of 𝑏 is simply the solution of the equation 𝑎ˣ = 𝑏.
Despite its simplicity, it has many useful properties that we take advantage of all the time.

You can think of the logarithm as the inverse of exponentiation.
Because of this, it turns multiplication into addition. Exponentiation does the opposite: it turns addition into multiplication.
(The base is often assumed to be a fixed constant. Thus, it can be omitted.)
Because of this, it turns multiplication into addition. Exponentiation does the opposite: it turns addition into multiplication.
(The base is often assumed to be a fixed constant. Thus, it can be omitted.)

Why is this useful? For calculating gradients and derivatives!
Training a neural network requires finding its gradient. However, lots of commonly used functions are written in terms of products.
As you can see, this complicates things.
Training a neural network requires finding its gradient. However, lots of commonly used functions are written in terms of products.
As you can see, this complicates things.

By taking the logarithm, we can compute the derivative as it turns products into sums.
This method is called logarithmic differentiation.
Since the logarithm is increasing, maximizing a function is the same as maximizing its logarithm. (Same with minimization.)
This method is called logarithmic differentiation.
Since the logarithm is increasing, maximizing a function is the same as maximizing its logarithm. (Same with minimization.)

One example where this is useful is the maximum likelihood estimation.
Given a set of observations and a predictive model, we can write this in the following form.
Given a set of observations and a predictive model, we can write this in the following form.

Believe it or not, this is behind the mean squared error.
Every time you use this, logarithms are working in the background.
Every time you use this, logarithms are working in the background.

If you enjoyed this thread and want to see behind the curtain of machine learning, I am writing a book for you, where we go from high school math to neural networks, one step at a time.
The early access for Mathematics of Machine Learning is out now!
tivadar.gumroad.com/l/mathematics-…
The early access for Mathematics of Machine Learning is out now!
tivadar.gumroad.com/l/mathematics-…
More applications of logarithms: transforming data for visualization. This is extremely useful in life sciences, where the scale of features is exponential.
https://twitter.com/jonathanalis1/status/1445493660737421322
And one more: numerical stability. When a computation involves very large numbers, taking the log can help avoid overflow.
https://twitter.com/kylewadegrove/status/1445472670435274753
• • •
Missing some Tweet in this thread? You can try to
force a refresh