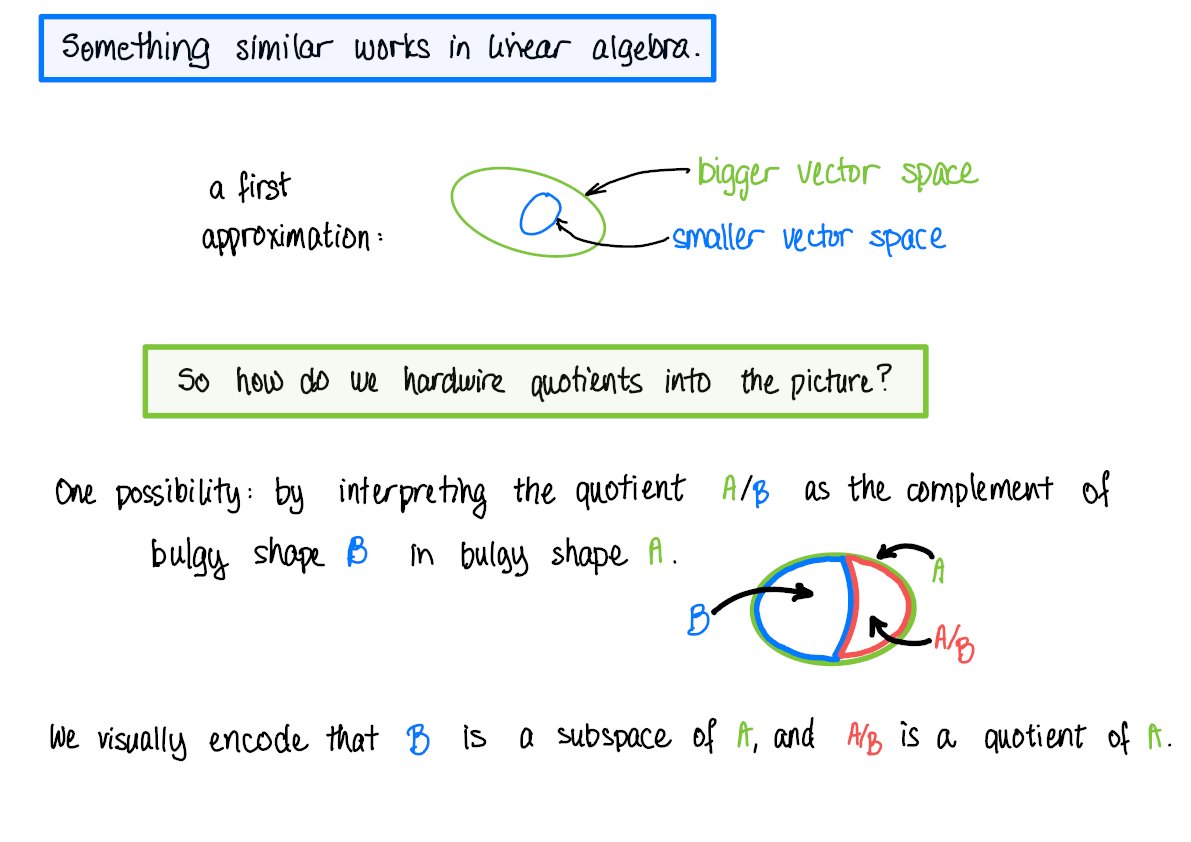
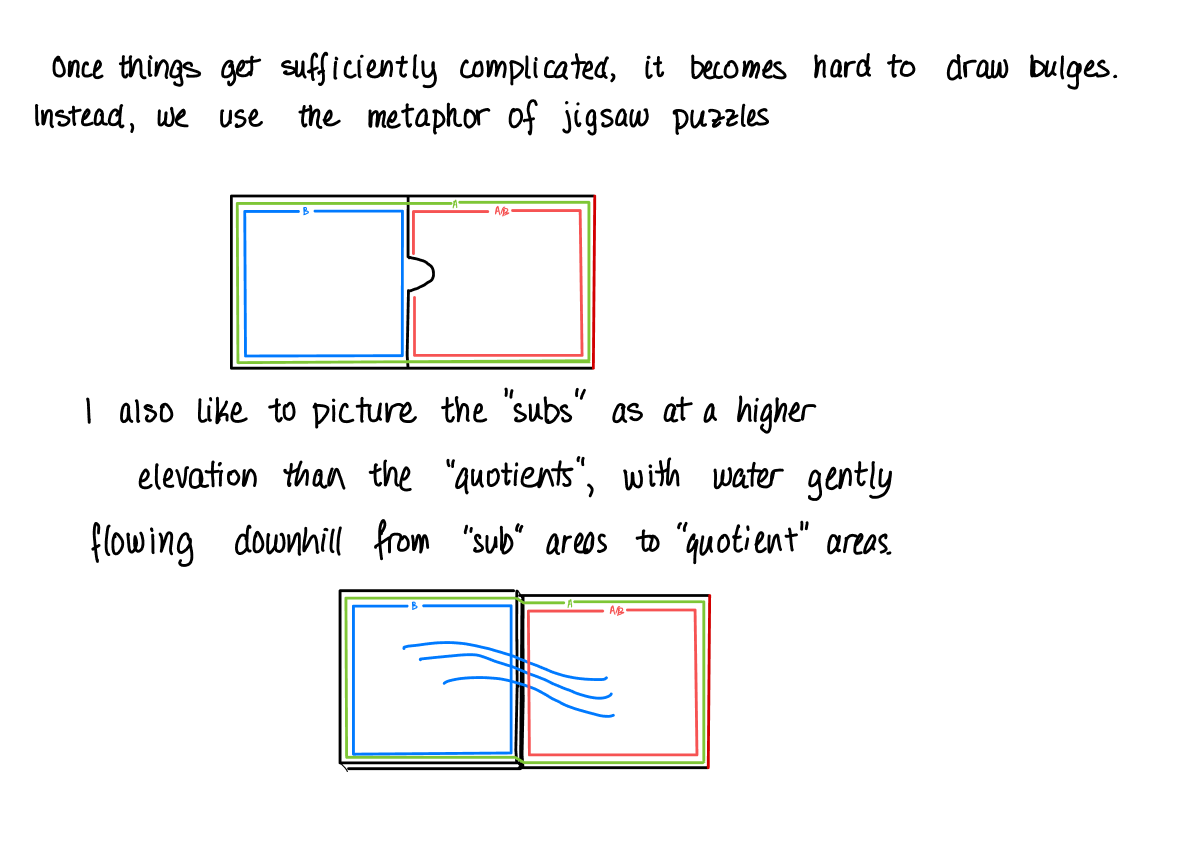
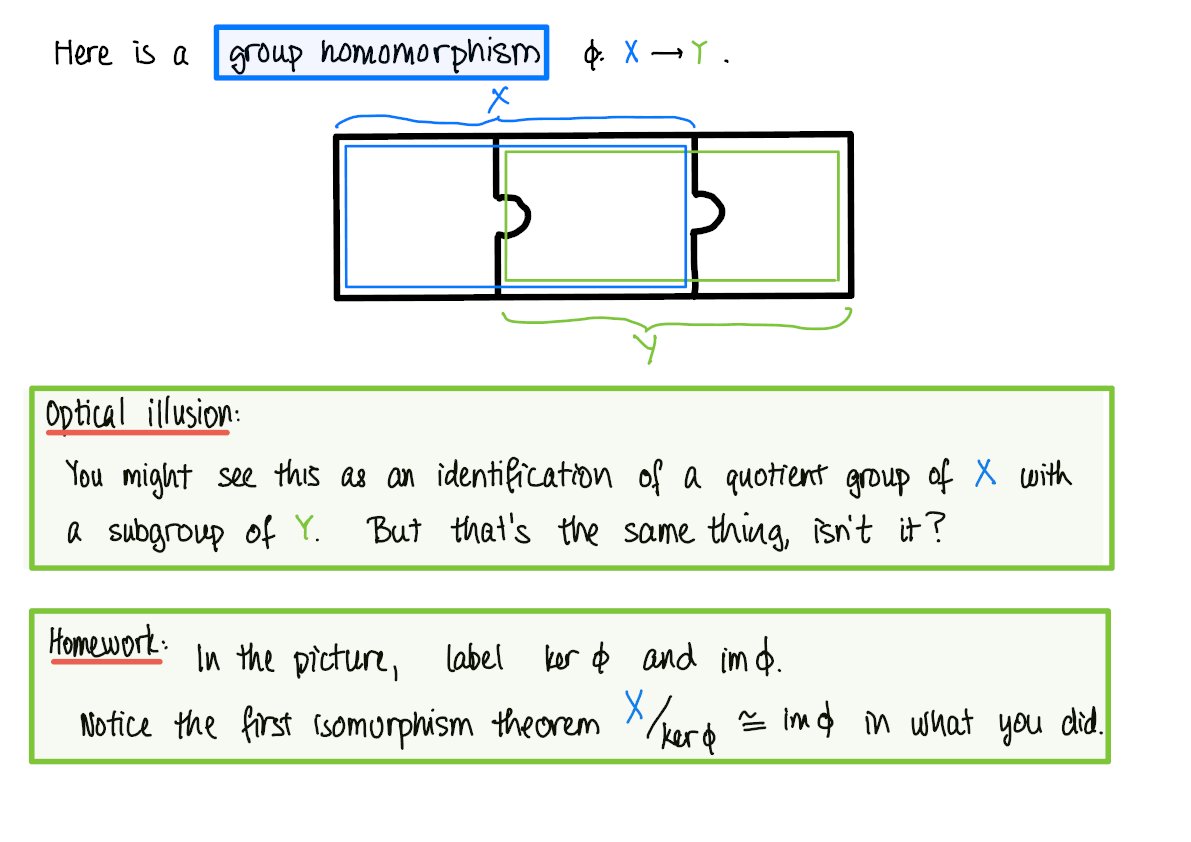
Niche/abstract topics rarely get highly illustrated explanations, much less in the form of a bedtime story.
A former prof of mine, Ravi Vakil, made this gem capturing how he thinks about exact sequences, cohomology, etc., which he kindly let me repost.
🧵
A former prof of mine, Ravi Vakil, made this gem capturing how he thinks about exact sequences, cohomology, etc., which he kindly let me repost.
🧵
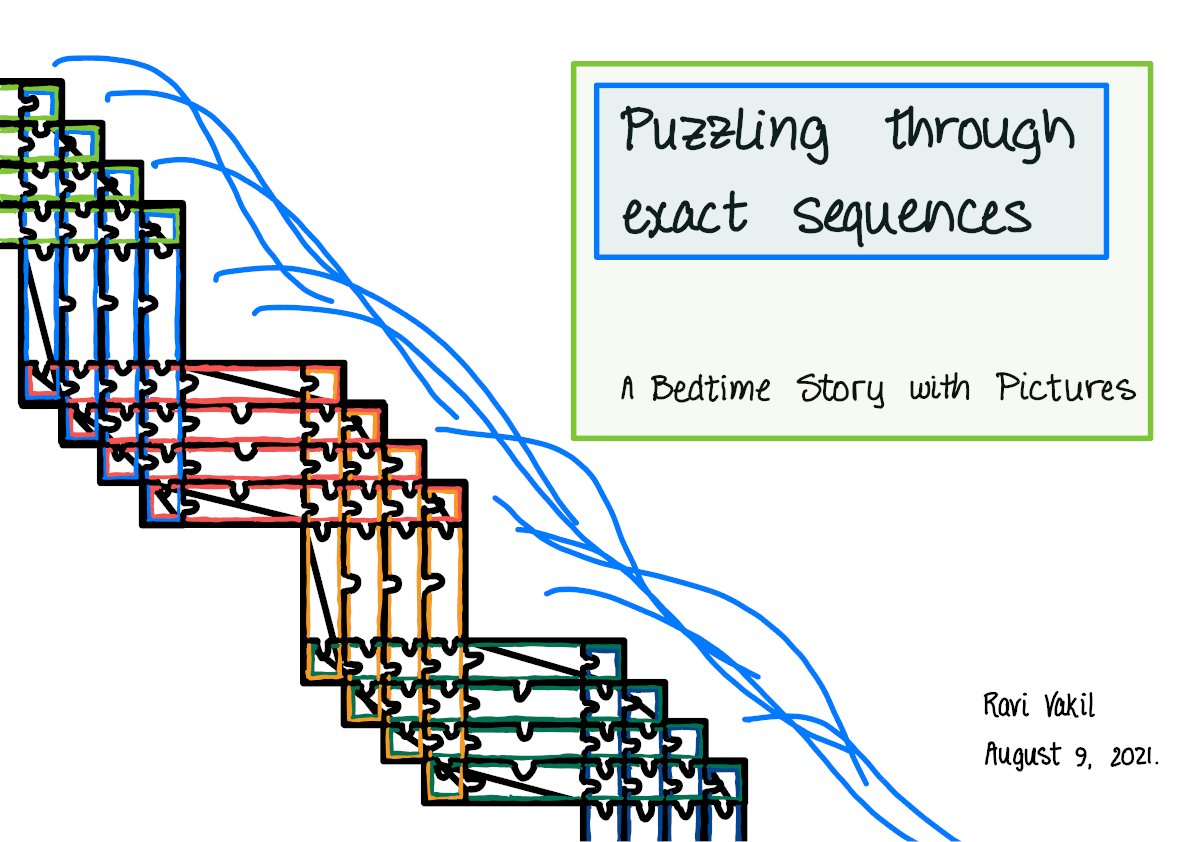
You can find the full story here: 3blue1brown.com/blog/exact-seq…
He goes on to talk about exact sequences, cohomology, and more. Admittedly, the audience is relatively niche, since it assumes you already know about those topics, but for the right person it certainly scratches an itch!
He goes on to talk about exact sequences, cohomology, and more. Admittedly, the audience is relatively niche, since it assumes you already know about those topics, but for the right person it certainly scratches an itch!
• • •
Missing some Tweet in this thread? You can try to
force a refresh