(Thread) Stochastic processes
Thought of posting a primer on stochastic processes that’ll be useful for any future posts on whether deriving Black’s formula for pricing calls/puts (my next post and should be a quick one) or discussing interpolation of vol surfaces (SVI) etc.
Thought of posting a primer on stochastic processes that’ll be useful for any future posts on whether deriving Black’s formula for pricing calls/puts (my next post and should be a quick one) or discussing interpolation of vol surfaces (SVI) etc.
This should also help understanding my VIX derivation post better.
Any let's get started.
Any underlying variable, be it a Nifty/BankNifty, USDINR, crude etc, can be represented as a stochastic process with a drift and a diffusion(random) component.
+
Any let's get started.
Any underlying variable, be it a Nifty/BankNifty, USDINR, crude etc, can be represented as a stochastic process with a drift and a diffusion(random) component.
+
Think of a stochastic process as a random variable evolving with time OR a collection of random variables that have been gathered at different times (Usually all stochastic processes, expectations are always defined under some probability measure but I’m not touching on
+
+
measures right now as it’ll complicate the topic under discussion. Will explain it in some future post).
The Weiner process or a standard Brownian motion is a fundamental unit to “drive” the diffusion component of an underlying variable.
So, what is a Weiner process? See below
+
The Weiner process or a standard Brownian motion is a fundamental unit to “drive” the diffusion component of an underlying variable.
So, what is a Weiner process? See below
+

A couple of more properties/applications of a Wiener processes in below pic.
Now that we defined a Wiener process let’s propose a typical stochastic differential equation (SDE) for a stock Index.
+
Now that we defined a Wiener process let’s propose a typical stochastic differential equation (SDE) for a stock Index.
+

Let’s work on the future/forward (these aren’t the same but let’s treat them for now without much harm) instead of spot to ignore the drift component. The SDE is in eq (1) below: 

Ito’s formula:
If we look at any function V of F_t i.e., V(F_t) and try writing a Taylor series expansion of it, and ignoring orders greater than two, we get the eq.2 below.
Here we assume V(F_t) is atleast twice-differentiable (i.e., second derivative is defined).
+
If we look at any function V of F_t i.e., V(F_t) and try writing a Taylor series expansion of it, and ignoring orders greater than two, we get the eq.2 below.
Here we assume V(F_t) is atleast twice-differentiable (i.e., second derivative is defined).
+

Difference here between standard calculus, where F is deterministic, and in this case where F is stochastic comes with how [dF_t ]^2 is treated. In standard calculus this term can be very small and often ignored. But with F_t stochastic let’s evaluate this term
+
+
.., also called "quadratic variation" of F_t also represented as 〖<F>〗_t:
From (1), see pic below.
That is the Ito’s formula for the index assumed to follow the SDE in (1)
In the next post I’ll derive the Black’s formula
(END)
From (1), see pic below.
That is the Ito’s formula for the index assumed to follow the SDE in (1)
In the next post I’ll derive the Black’s formula
(END)
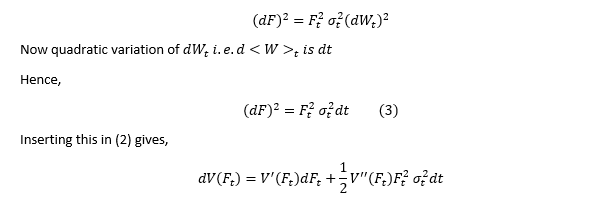
• • •
Missing some Tweet in this thread? You can try to
force a refresh




