
1/
Get a cup of coffee.
In this thread, I'll help you understand Escape Velocity -- a super interesting physics concept that can also teach us some valuable life lessons.
Get a cup of coffee.
In this thread, I'll help you understand Escape Velocity -- a super interesting physics concept that can also teach us some valuable life lessons.
2/
Let's start with 2 everyday physics facts.
Fact 1. If we toss a ball up into the air, it comes back down after a while.
Fact 2. If we put in some more effort and send the ball up faster, it still falls back down. But this time, it travels further and takes longer.
Let's start with 2 everyday physics facts.
Fact 1. If we toss a ball up into the air, it comes back down after a while.
Fact 2. If we put in some more effort and send the ball up faster, it still falls back down. But this time, it travels further and takes longer.
3/
So, here's a question:
Is it possible to toss our ball up with *such* high speed that it NEVER comes back down?
That is, our ball somehow escapes Earth's gravity and wanders off into outer space.
Kinda like @SahilBloom's (alleged) grand slam:
So, here's a question:
Is it possible to toss our ball up with *such* high speed that it NEVER comes back down?
That is, our ball somehow escapes Earth's gravity and wanders off into outer space.
Kinda like @SahilBloom's (alleged) grand slam:

4/
IF this is indeed possible, then what's the *lowest* speed we can give our ball so that it escapes Earth?
(It's reasonably evident that any speed *above* this cutoff will also work, if the goal is simply to escape Earth.)
This "cutoff speed" is called Escape Velocity.
IF this is indeed possible, then what's the *lowest* speed we can give our ball so that it escapes Earth?
(It's reasonably evident that any speed *above* this cutoff will also work, if the goal is simply to escape Earth.)
This "cutoff speed" is called Escape Velocity.
5/
Finding our ball's Escape Velocity is clearly a physics question.
And it has something to do with gravity.
So, Newton's Law of Gravitation seems like a good place to start our search.
Here is Newton's Law, applied to our example:
Finding our ball's Escape Velocity is clearly a physics question.
And it has something to do with gravity.
So, Newton's Law of Gravitation seems like a good place to start our search.
Here is Newton's Law, applied to our example:

6/
Newton's Law is an example of "Inverse Square" behavior:
The force of gravity goes down as the *square* of the ball's distance from the center of the Earth.
Double this distance, and the force of gravity becomes a fourth of what it was. Triple it, and it becomes a ninth.
Newton's Law is an example of "Inverse Square" behavior:
The force of gravity goes down as the *square* of the ball's distance from the center of the Earth.
Double this distance, and the force of gravity becomes a fourth of what it was. Triple it, and it becomes a ninth.
7/
Physics is full of such Inverse Square Laws.
For example, Coulomb's Law of Electrostatics (ie, the force with which electric charges attract and repel each other) is Inverse Square.
And so are laws that describe the intensity of light and other electromagnetic radiation.
Physics is full of such Inverse Square Laws.
For example, Coulomb's Law of Electrostatics (ie, the force with which electric charges attract and repel each other) is Inverse Square.
And so are laws that describe the intensity of light and other electromagnetic radiation.

8/
For our problem, Inverse Squared-ness has the following consequence:
As our ball goes higher and higher, Earth's gravitational pull on it gets weaker and weaker.
So, our ball's *acceleration* (ie, how much its speed changes from second to second) *decreases* on its way up.
For our problem, Inverse Squared-ness has the following consequence:
As our ball goes higher and higher, Earth's gravitational pull on it gets weaker and weaker.
So, our ball's *acceleration* (ie, how much its speed changes from second to second) *decreases* on its way up.
9/
In other words:
On the way up, our ball's speed decreases with time.
This decrease is greatest during the first second, a little smaller during the second second, and so on.
(And on the way down, it's the other way round: the ball's speed increases faster and faster.)
In other words:
On the way up, our ball's speed decreases with time.
This decrease is greatest during the first second, a little smaller during the second second, and so on.
(And on the way down, it's the other way round: the ball's speed increases faster and faster.)
10/
Newton's Law can be used to derive a system of *Differential Equations*.
Like so:
(Please don't worry if you don't get this math. I promise you won't need it to understand the rest of this thread.)
Newton's Law can be used to derive a system of *Differential Equations*.
Like so:
(Please don't worry if you don't get this math. I promise you won't need it to understand the rest of this thread.)

11/
The *power* of these Differential Equations is that we can simulate them on a computer.
That means: knowing just the initial speed we give our ball, the computer can tell us our ball's entire trajectory -- its distance, speed, acceleration, etc., throughout its flight.
The *power* of these Differential Equations is that we can simulate them on a computer.
That means: knowing just the initial speed we give our ball, the computer can tell us our ball's entire trajectory -- its distance, speed, acceleration, etc., throughout its flight.
12/
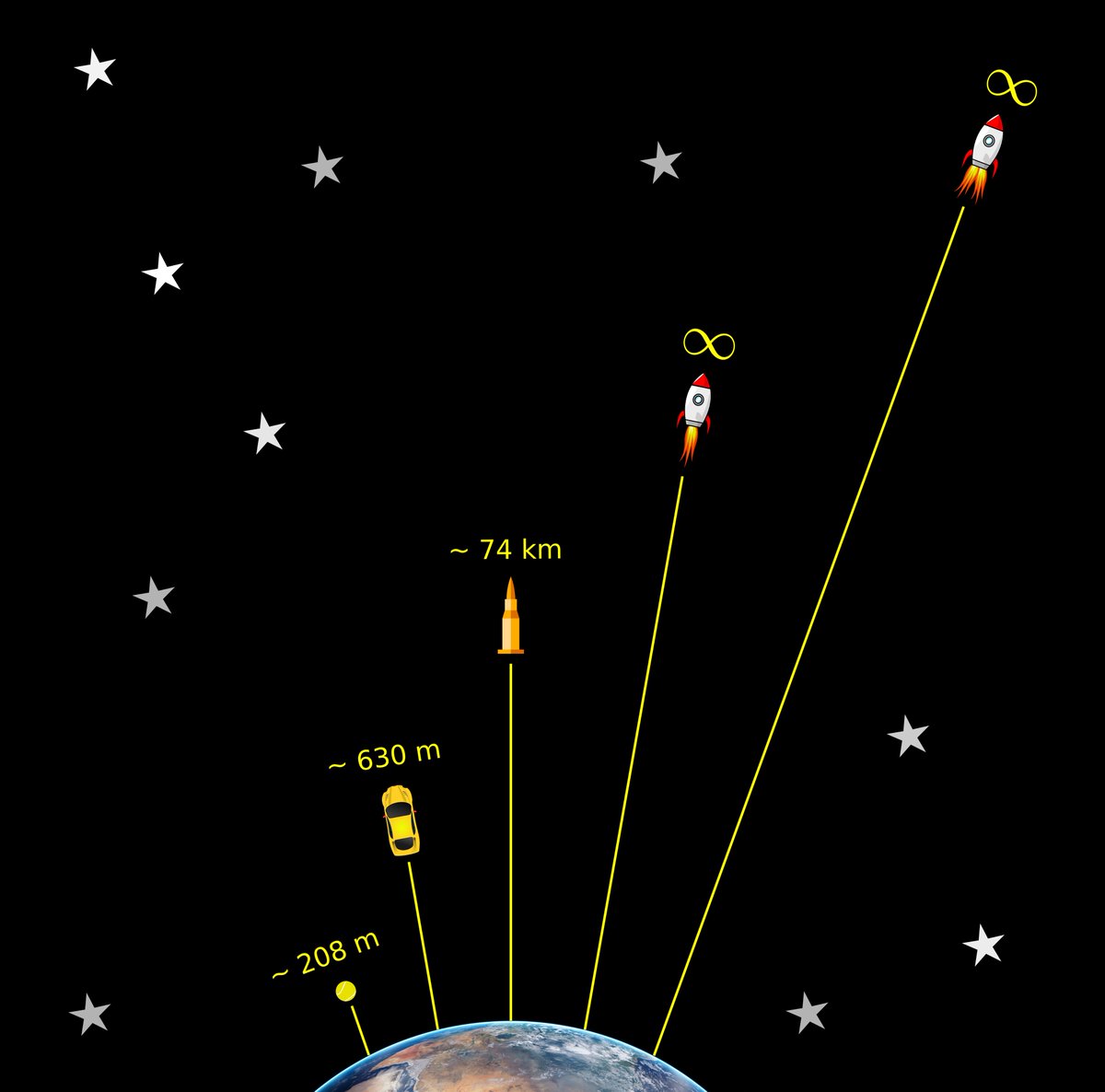
For example, @rogerfederer's fastest recorded serve was at 230 km/hr (~63.89 m/s).
If we tossed our ball at this speed straight up, the ball will rise ~208 meters and come back to Earth in ~13 seconds.
Here's its computer simulated trajectory:
For example, @rogerfederer's fastest recorded serve was at 230 km/hr (~63.89 m/s).
If we tossed our ball at this speed straight up, the ball will rise ~208 meters and come back to Earth in ~13 seconds.
Here's its computer simulated trajectory:
13/
Let's take another example.
The upcoming Tesla Roadster is expected to have a top speed of ~250 mph (~111.11 m/s).
If we tossed an object with this speed straight up, it will rise ~630 meters, and then fall back to us in ~22.7 seconds:
Let's take another example.
The upcoming Tesla Roadster is expected to have a top speed of ~250 mph (~111.11 m/s).
If we tossed an object with this speed straight up, it will rise ~630 meters, and then fall back to us in ~22.7 seconds:
14/
So, IF escape is possible, it's going to take more than ~250 mph.
So, let's try something *even* faster: a speeding bullet.
Sadly, even a really fast bullet (fired at 1,200 m/s) cannot escape Earth. It goes far (~74 kilometers), but ultimately comes crashing down.
So, IF escape is possible, it's going to take more than ~250 mph.
So, let's try something *even* faster: a speeding bullet.
Sadly, even a really fast bullet (fired at 1,200 m/s) cannot escape Earth. It goes far (~74 kilometers), but ultimately comes crashing down.
15/
These examples make us wonder: is escape even possible?
After all, no matter how fast we shoot an object up, Earth's relentless gravitational pull *will* continuously keep slowing it down.
These examples make us wonder: is escape even possible?
After all, no matter how fast we shoot an object up, Earth's relentless gravitational pull *will* continuously keep slowing it down.
16/
And if our object *keeps* slowing down, it's eventually going to lose ALL its speed, right?
And once that happens, there's no choice. Our object HAS to come crashing down. Right?
This logic would make it seem like escape is impossible.
And if our object *keeps* slowing down, it's eventually going to lose ALL its speed, right?
And once that happens, there's no choice. Our object HAS to come crashing down. Right?
This logic would make it seem like escape is impossible.
17/
But thankfully, this logic is incorrect.
Escape is possible.
And we have the Inverse Squared-ness of Newton's Law to thank for it.
IF the Earth exerted a *constant* pull -- ie, the SAME force no matter how far away the object is -- escape would indeed be impossible.
But thankfully, this logic is incorrect.
Escape is possible.
And we have the Inverse Squared-ness of Newton's Law to thank for it.
IF the Earth exerted a *constant* pull -- ie, the SAME force no matter how far away the object is -- escape would indeed be impossible.
18/
But Earth's pull is NOT constant.
It *weakens* as the object gets further away -- ie, Inverse Squared-ness.
This makes it possible to launch an object that *always* keeps slowing down but *never* comes to a complete stop.
But Earth's pull is NOT constant.
It *weakens* as the object gets further away -- ie, Inverse Squared-ness.
This makes it possible to launch an object that *always* keeps slowing down but *never* comes to a complete stop.
19/
And that's what "escape" looks like.
Our object will NEVER be entirely free of Earth's pull.
But the pull will keep weakening.
And IF our object is launched with sufficient speed, it will ALWAYS have enough energy to *overcome* Earth's pull.
And that's what "escape" looks like.
Our object will NEVER be entirely free of Earth's pull.
But the pull will keep weakening.
And IF our object is launched with sufficient speed, it will ALWAYS have enough energy to *overcome* Earth's pull.
20/
Physicists have a neat trick to calculate Escape Velocity in this sense.
They call it "The Law Of Conservation Of Energy".
Here's the math:
(Please don't worry if you don't get this math. Just register the formula for Escape Velocity in the box at the end.)

Physicists have a neat trick to calculate Escape Velocity in this sense.
They call it "The Law Of Conservation Of Energy".
Here's the math:
(Please don't worry if you don't get this math. Just register the formula for Escape Velocity in the box at the end.)


21/
Intuitively, Energy Conservation works like this:
At launch, our object has some energy.
Over time, part of this energy is "used up" to overcome the pull of Earth's gravity.
Intuitively, Energy Conservation works like this:
At launch, our object has some energy.
Over time, part of this energy is "used up" to overcome the pull of Earth's gravity.
22/
"Escape" means there should ALWAYS be at least *some* energy "left over" -- AFTER overcoming gravity.
This "left over" energy should never go to zero in any finite amount of time. If it does, the object will come crashing down.
"Escape" means there should ALWAYS be at least *some* energy "left over" -- AFTER overcoming gravity.
This "left over" energy should never go to zero in any finite amount of time. If it does, the object will come crashing down.
23/
So, Escape just means *seeding* the object with enough energy at the start.
This is achieved by launching it with a speed greater than Escape Velocity (~11,183 m/s).
No wonder even our ~1,200 m/s bullet came back down. Escape Velocity for Earth is more than 9x that!
So, Escape just means *seeding* the object with enough energy at the start.
This is achieved by launching it with a speed greater than Escape Velocity (~11,183 m/s).
No wonder even our ~1,200 m/s bullet came back down. Escape Velocity for Earth is more than 9x that!
24/
What's remarkable is that our Escape Velocity calculated using this model (~11,183 m/s) is the SAME for ALL objects on Earth -- regardless of their mass, size, etc.
Whether we want to launch a mouse or an elephant into space, we give it a speed > ~11,183 m/s.
What's remarkable is that our Escape Velocity calculated using this model (~11,183 m/s) is the SAME for ALL objects on Earth -- regardless of their mass, size, etc.
Whether we want to launch a mouse or an elephant into space, we give it a speed > ~11,183 m/s.
25/
FYI: There are some caveats with our Escape Velocity model.
For example, we ignore air resistance.
We also ignore the possibility that the launched object itself may be capable of energy generation/propelling/steering (eg, by burning rocket fuel).
And so on.
FYI: There are some caveats with our Escape Velocity model.
For example, we ignore air resistance.
We also ignore the possibility that the launched object itself may be capable of energy generation/propelling/steering (eg, by burning rocket fuel).
And so on.
26/
Beyond math and physics, Escape Velocity can teach us some life lessons.
Lesson 1: Be conscious of abrupt "tipping points" or "phase transitions".
At its core, that's what Escape Velocity is. An *abrupt* transition between two completely different kinds of behavior.
Beyond math and physics, Escape Velocity can teach us some life lessons.
Lesson 1: Be conscious of abrupt "tipping points" or "phase transitions".
At its core, that's what Escape Velocity is. An *abrupt* transition between two completely different kinds of behavior.
27/
Launch an object slower than Escape Velocity, and it comes crashing down.
But launch it just a little faster, and it keeps going up forever.
Thus, we get 2 completely different behaviors -- out of just a tiny change in initial condition.
Launch an object slower than Escape Velocity, and it comes crashing down.
But launch it just a little faster, and it keeps going up forever.
Thus, we get 2 completely different behaviors -- out of just a tiny change in initial condition.
28/
Lots of non-linear systems exhibit this kind of dynamic.
For example, if the world believes that a business is on one side of a tipping point, but we (correctly) figure out that it's on the *other* side, there could be a lot of money in it.
Lots of non-linear systems exhibit this kind of dynamic.
For example, if the world believes that a business is on one side of a tipping point, but we (correctly) figure out that it's on the *other* side, there could be a lot of money in it.
29/
For example, in ~1963, during the Salad Oil Crisis, the world left American Express for dead.
But Buffett figured out that the company had enough "energy" (balance sheet strength, cash flows, loyal customers, etc.) to overcome the crisis. He bought the stock and cleaned up.
For example, in ~1963, during the Salad Oil Crisis, the world left American Express for dead.
But Buffett figured out that the company had enough "energy" (balance sheet strength, cash flows, loyal customers, etc.) to overcome the crisis. He bought the stock and cleaned up.
30/
Lesson 2: Always keep moving (in the right direction), even if it's only small steps.
There are usually many forces (like gravity) that are always looking to pull us down.
It takes continuous energy and work to keep overcoming these forces.
Lesson 2: Always keep moving (in the right direction), even if it's only small steps.
There are usually many forces (like gravity) that are always looking to pull us down.
It takes continuous energy and work to keep overcoming these forces.
31/
The moment we stop moving/striving against these forces, we risk succumbing to them.
Just like an object that has exhausted its energy and therefore has to come crashing back to Earth.
In this context, I love this thoughtful nugget from @JeffBezos's 2020 letter:

The moment we stop moving/striving against these forces, we risk succumbing to them.
Just like an object that has exhausted its energy and therefore has to come crashing back to Earth.
In this context, I love this thoughtful nugget from @JeffBezos's 2020 letter:


32/
Lesson 3: The first step is usually the hardest.
In our Escape Velocity example, objects always expend the maximum amount of energy against Earth to move the first meter.
The second meter is slightly easier than the first.
The third is easier than the second.
And so on.
Lesson 3: The first step is usually the hardest.
In our Escape Velocity example, objects always expend the maximum amount of energy against Earth to move the first meter.
The second meter is slightly easier than the first.
The third is easier than the second.
And so on.
33/
I think this applies to many things in life -- eating right, exercising, getting started with investing, etc.
The first few steps tend to be the hardest.
After that, powerful forces like habit, momentum, inertia, compounding, etc., tend to kick in.
I think this applies to many things in life -- eating right, exercising, getting started with investing, etc.
The first few steps tend to be the hardest.
After that, powerful forces like habit, momentum, inertia, compounding, etc., tend to kick in.
34/
If you want to learn more about Escape Velocity, or other physics topics, I can recommend the NCERT textbooks that I studied from in high school.
They're available for free online.
Link: ncert.nic.in/textbook.php?k…
Here's the Escape Velocity section from these books:

If you want to learn more about Escape Velocity, or other physics topics, I can recommend the NCERT textbooks that I studied from in high school.
They're available for free online.
Link: ncert.nic.in/textbook.php?k…
Here's the Escape Velocity section from these books:


35/
I'll leave you with this fun problem about black holes and Escape Velocities.
Please leave a comment with your answer!
I'll leave you with this fun problem about black holes and Escape Velocities.
Please leave a comment with your answer!

36/
Thank you very much for patiently reading all the way to the end.
I hope all your investments attain Escape Velocity and make it to the moon. 🚀🚀
Please stay safe. Enjoy your weekend!
/End
Thank you very much for patiently reading all the way to the end.
I hope all your investments attain Escape Velocity and make it to the moon. 🚀🚀
Please stay safe. Enjoy your weekend!
/End
• • •
Missing some Tweet in this thread? You can try to
force a refresh












