Thread by @swapnakpanda

💙 Matrix implementation in JavaScript

Let's learn through this 🧵

⇩

0️⃣ Introduction

Matrix is a 2-dimensional Array arrangement of numbers.

Example:
[[a₁₁, a₁₂, a₁₃],
[a₂₁, a₂₂, a₂₃],
[a₃₁, a₃₂, a₃₃]]

✪ Element: Each item in the inner array is called an element of the matrix. Eg, a₁₁

✪ Row: Each item in the main array is called a row. Eg, [a₁₁, a₁₂, a₁₃]

✪ Column: A column is list of items at a specific index from each row in order. Eg, [a₁₁, a₂₁, a₃₁]

1️⃣ Dimension of a Matrix

Dimension of a Matrix is specified as the number of rows and number of columns in the matrix.

2️⃣ Square Matrix

A matrix is called as a "Square Matrix" only if its "number of rows" is equal to its "number of columns".

3️⃣ Diagonal Matrix

A "Diagonal Matrix" is a square matrix which has only Zeroes (0s) as its non-diagonal elements (row index = column index).

Diagonal elements can be both Non-Zero and Zero.

4️⃣ Upper Triangular Matrix

An "Upper Triangular Matrix" is a square matrix which has only Zeroes (0s) as elements "below" the diagonal elements.

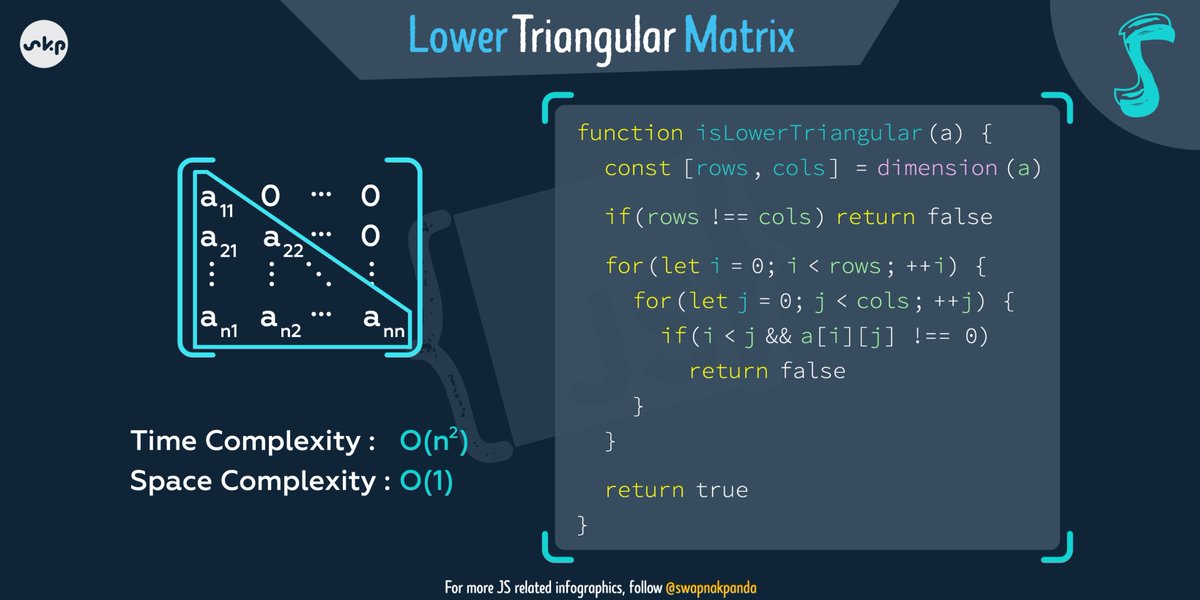
5️⃣ Lower Triangular Matrix

An "Lower Triangular Matrix" is a square matrix which has only Zeroes (0s) as elements "above" the diagonal elements.

6️⃣ Identity/Unity Matrix

An "Identity Matrix" is a diagonal matrix with only 1s as its diagonal elements.

7️⃣ Zero Matrix

A "Zero Matrix" has only Zeroes (0s) as all its elements.

8️⃣ Transpose Matrix

A "Transpose Matrix" is formed by converting rows of a matrix into columns (and thus columns into rows).

Dimension of a transpose matrix is exactly opposite of the dimension of the original matrix.

9️⃣ Scalar Multiplication

By doing "Scalar Multiplication", each element of the matrix is multiplied by a scalar value.

1️⃣0️⃣ Matrix Addition

By "Matrix Addition", elements at a specific row and column from 2 matrices are added.

1️⃣1️⃣ Matrix Subtraction

By "Matrix Subtraction", elements at a specific row and column from one matrix is subtracted from the another.

1️⃣2️⃣ Matrix Multiplication

By "Matrix Multiplication", elements of a row from the first matrix is first multiplied with elements of a column from the second matrix and then summation is taken.

1️⃣3️⃣ Orthogonal Matrix

A matrix is known as "Orthogonal" when multiplied with its transpose results into an Identity Matrix.

In other words, if transpose of a matrix is equivalent to its inverse, the matrix is orthogonal.

OMISSIONS:

✪ Determinant of a Matrix
✪ Inverse of a Matrix

Because of their complex algorithms which won't fit into an infographic, I omitted these two.

Are you interested in JavaScript contents? I am sharing a lot of materials in Infographics.

All organised in a “Twitter Moment”, 👇

twitter.com/i/events/14358…