En #matemáticas, la forma en que representamos un determinado concepto, puede facilitar su comprensión y ayudar a establecer conexiones con otros conceptos. Por eso, estos días estamos usando esta representación geométrica para algunos números irracionales. 
No tiene ningún secreto, simplemente se trata de tomar como unidad de longitud el lado de los cuadraditos de las cuadrícula y construir segmentos que midan una cantidad irracional de unidades, mediante la aplicación del Teorema de Pitágoras.
El uso de la cuadrícula facilita la interpretación de estas cantidades, a partir de las áreas de los cuadrados construidos sobre estos segmentos. √2 es la longitud del lado de un cuadrado de área igual a 2 cuadraditos; √5 es el lado de un cuadrado de área 5, etc.
Por supuesto, esta representación tiene grandes limitaciones, ya que no se puede construir cualquier radical, como segmento con extremos sobre puntos de la cuadrícula. Solo se pueden representar aquellos cuyo radicando se pueda expresar como suma de dos cuadrados.
Sin embargo, los casos que sí se pueden representar de esta manera, permiten visualizar de manera intuitiva algunas propiedades y relaciones entre radicales.
Por ejemplo, resulta muy fácil identificar si dos radicales son equivalentes, es decir múltiplos de un mismo radical, ya que, en dicho caso, los segmentos correspondientes son paralelos.
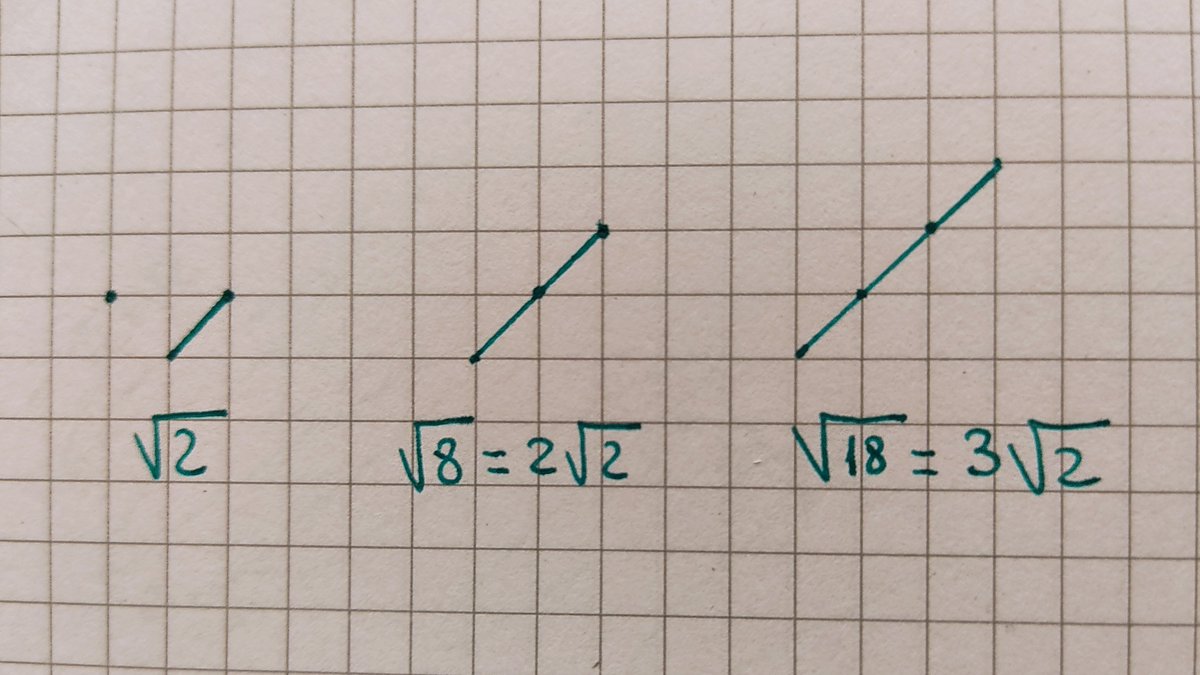
También podemos visualizar claramente que la suma de dos radicales no se puede obtener sumando los radicandos, ya que las longitudes de los segmentos correspondientes son claramente distintas.
En lo que se refiere a la suma, se ve de manera natural que la suma de dos radicales semejantes se puede expresar como un único radical cuyo coeficiente es igual a la suma de los coeficientes de los sumandos, ya que en este caso, los segmentos correspondientes quedan alineados.
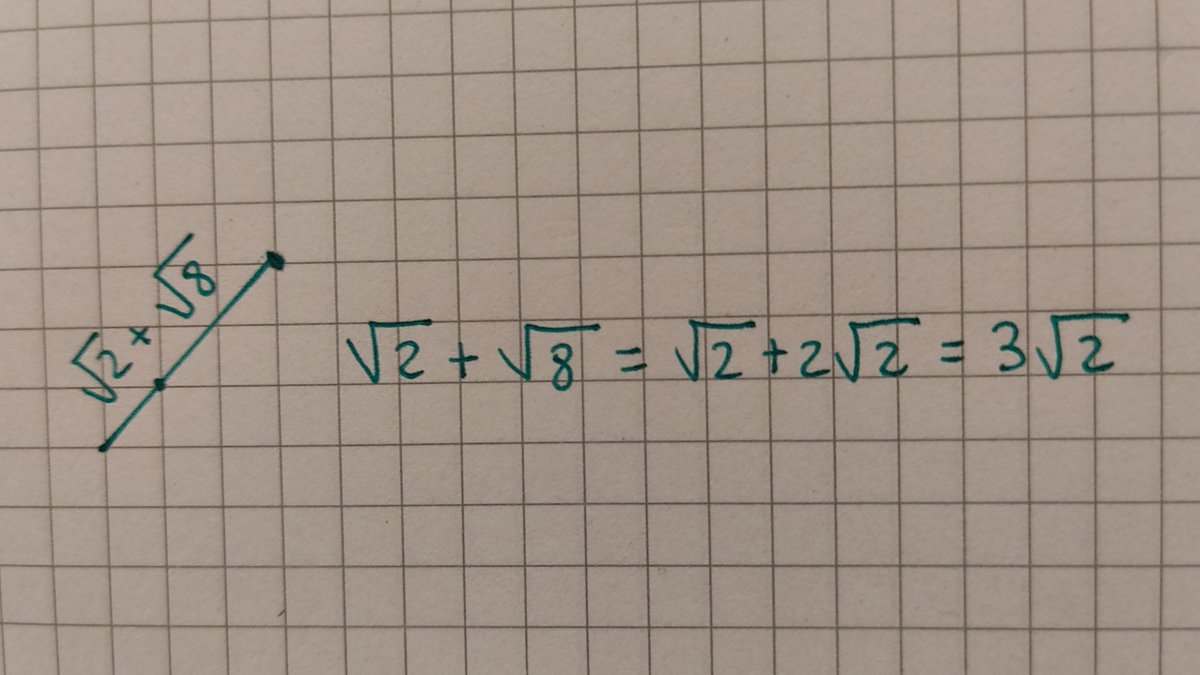
En cambio, cuando los radicales no son semejantes, al no estar claro cómo se pueden combinar las dos cantidades, lo más natural es dejar la suma indicada.
Hay otros errores comunes, que son fruto de una mala comprensión de la operaciones. Por ejemplo: 2+√2=2√2. Este tipo de representación ayuda a desmontarlos.
La multiplicación de dos radicales semejantes se puede interpretar como el área del rectángulo definido por los dos segmentos correspondientes, ya que, en este caso, dichos segmentos son perpendiculares. (¿Por qué?)
Si los radicales no son semejantes, ya no definen un rectángulo, sino un romboide. Entonces, su área representa una cota inferior del producto de dichos radicales.
Estas son algunas de las cuestiones que me han parecido interesantes de este tipo de representación. He propuesto a un par de alumnas que investiguen si ofrece algo más, o si se puede ampliar para incorporar el resto de radicales. A ver si hay alguna sorpresa.
CORRECCIÓN: Aquí la representación corregida sin el error de √45.
Hoy en clase, esta representación también nos ha facilitado realizar sumas entre cantidades enteras y radicales.
• • •
Missing some Tweet in this thread? You can try to
force a refresh
