Thread by @TivadarDanka

What is recursion?

A concise guide from zero to one. 100% knowledge, 0% fluff. 🠓

1/13

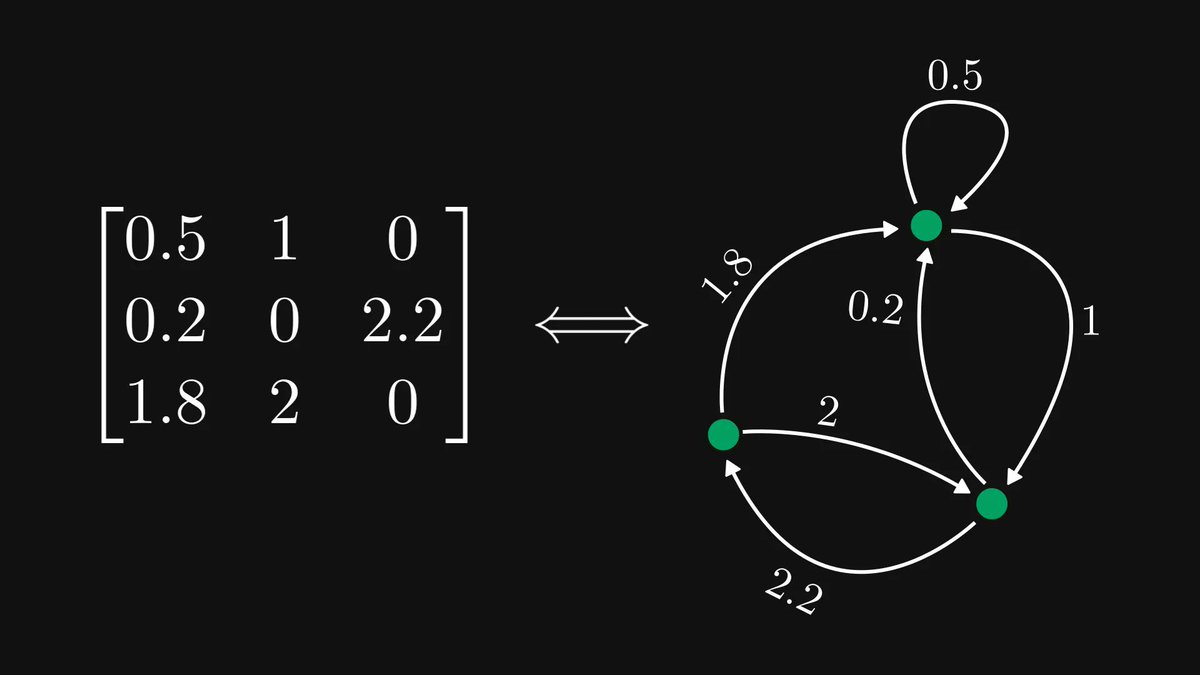
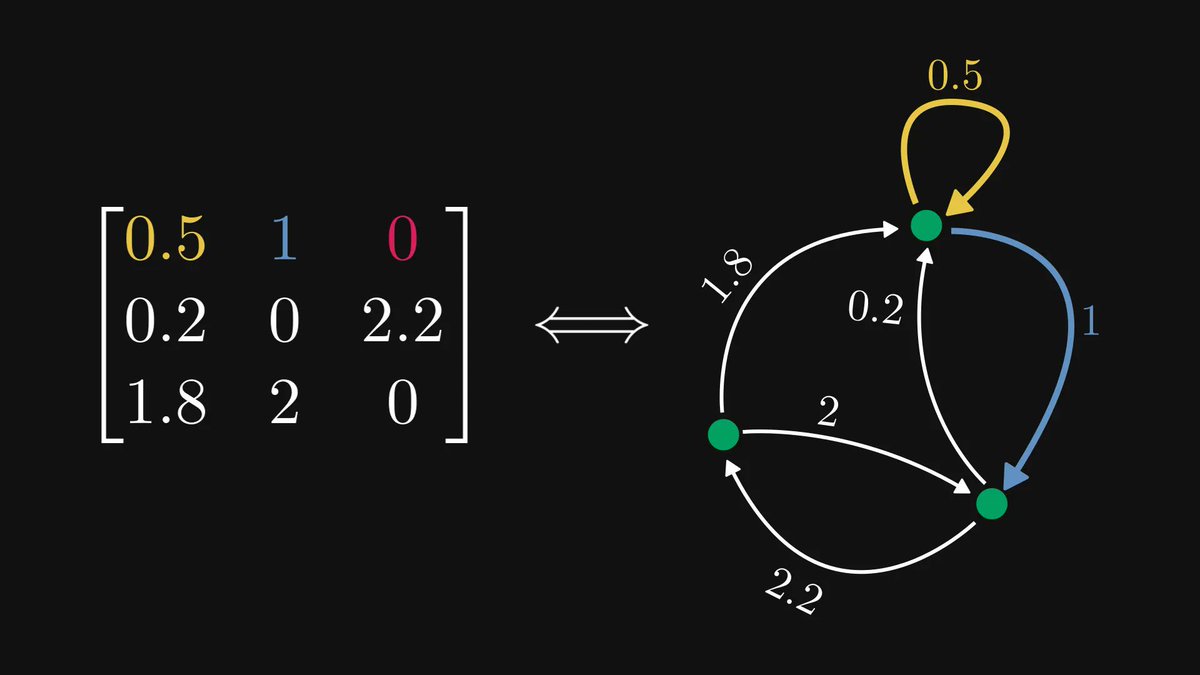
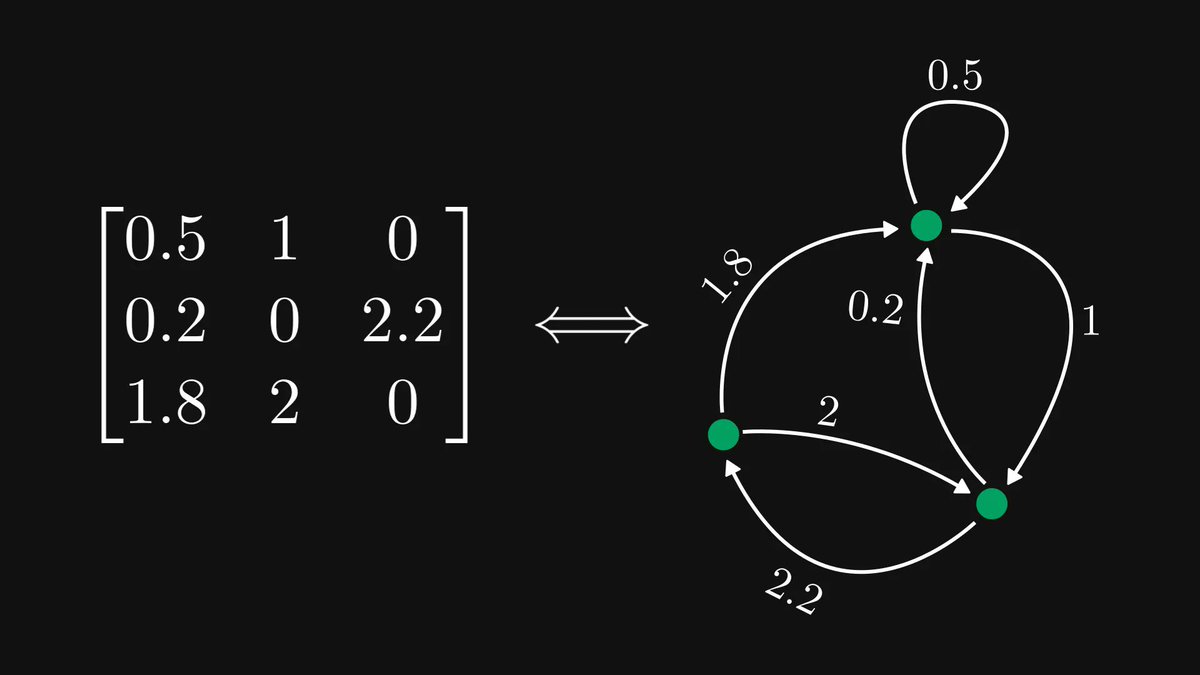
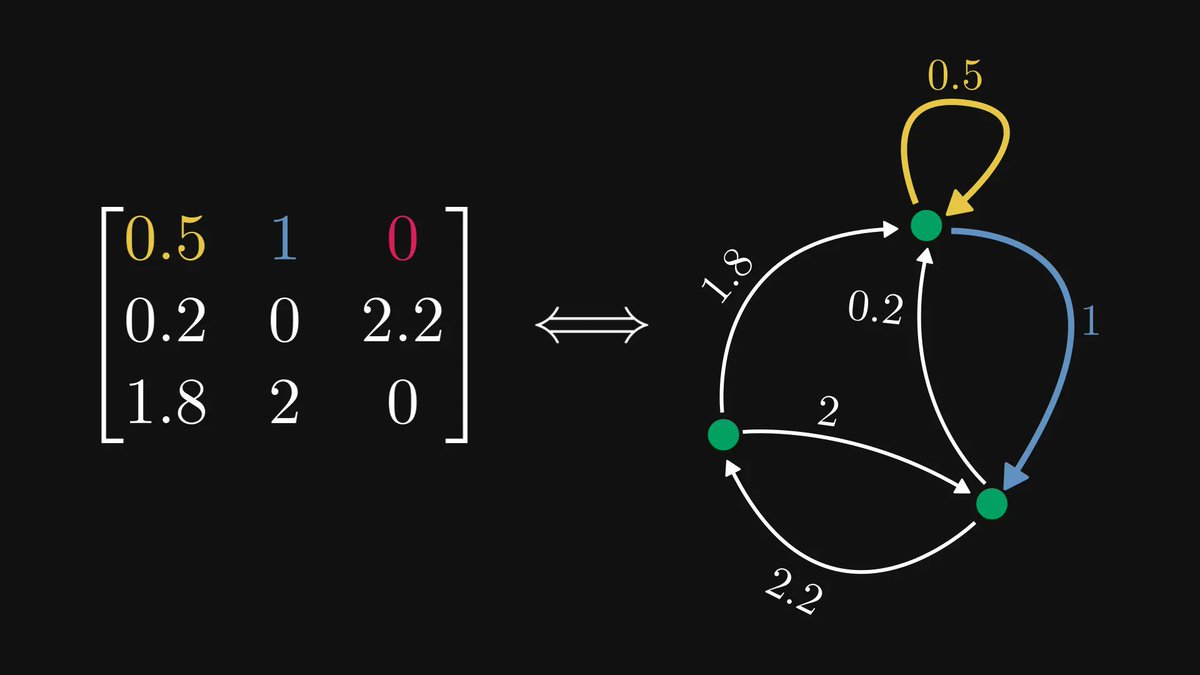
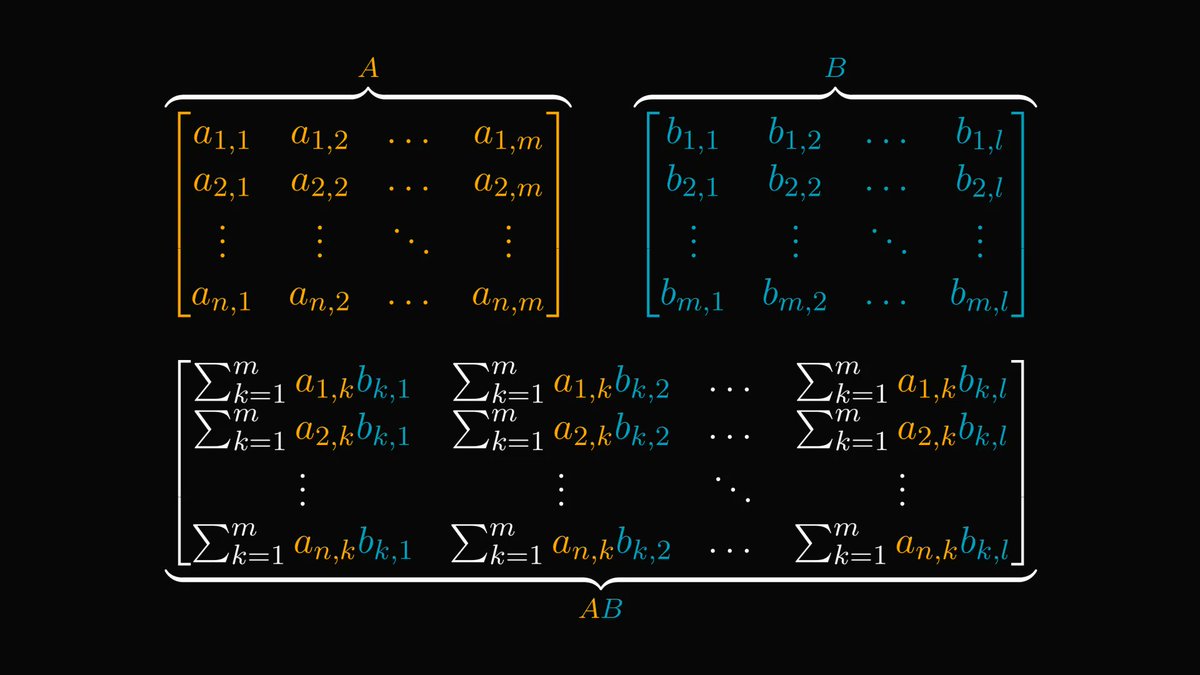
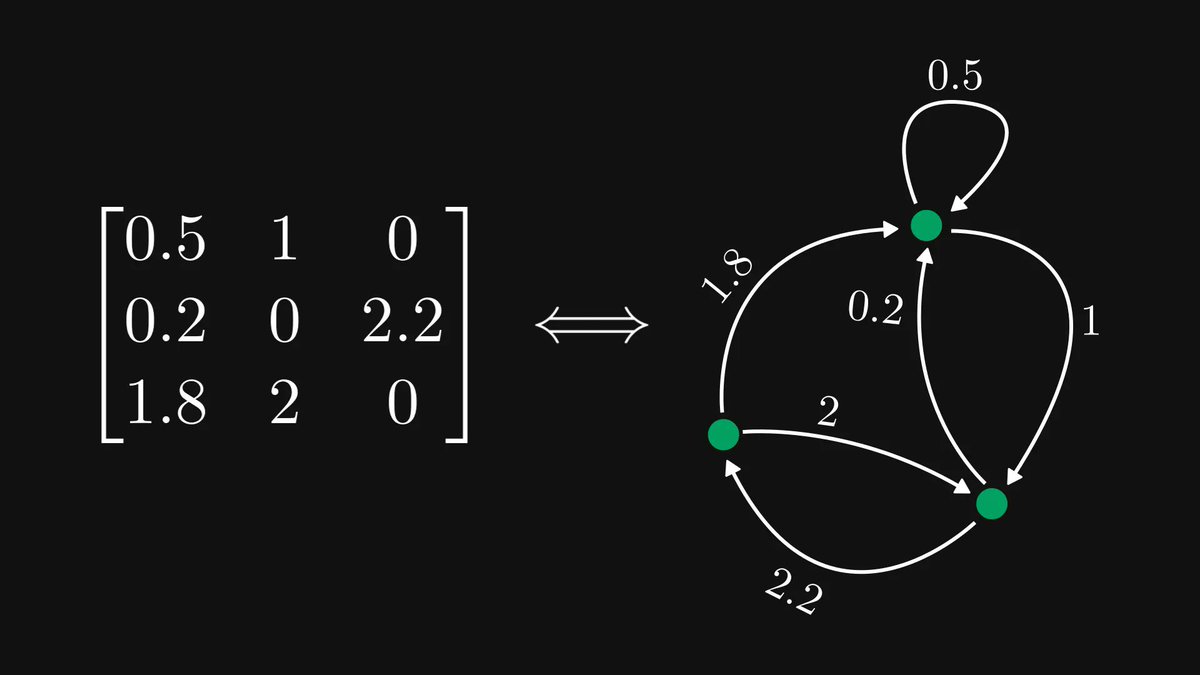
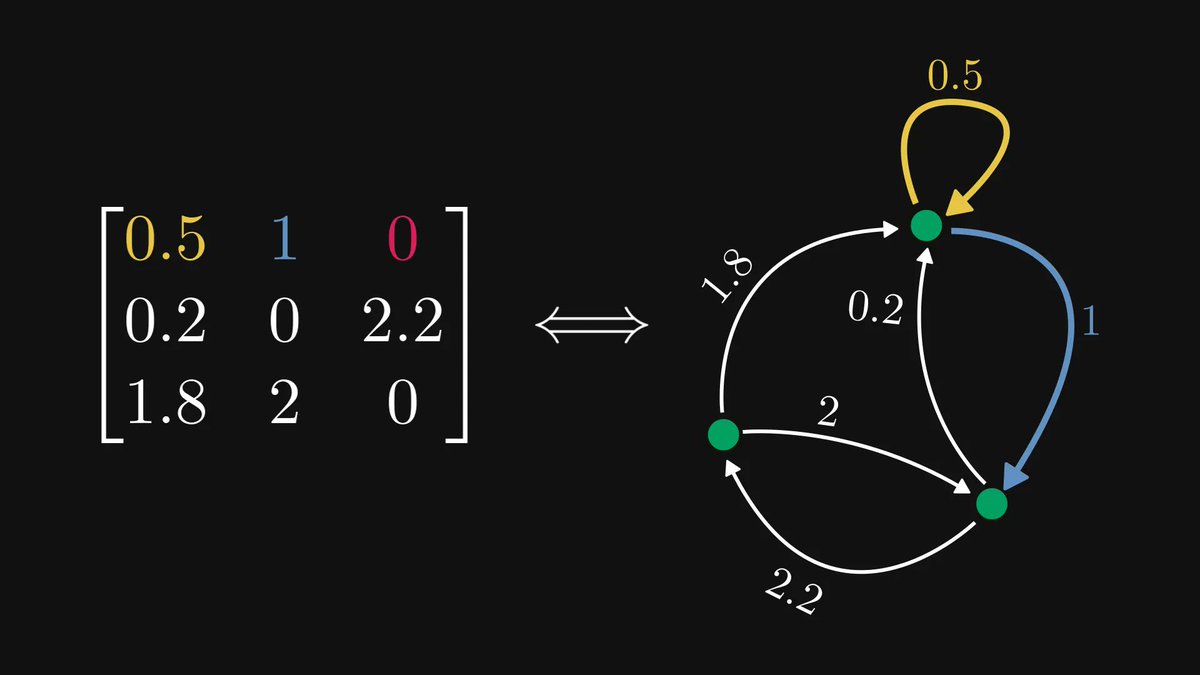
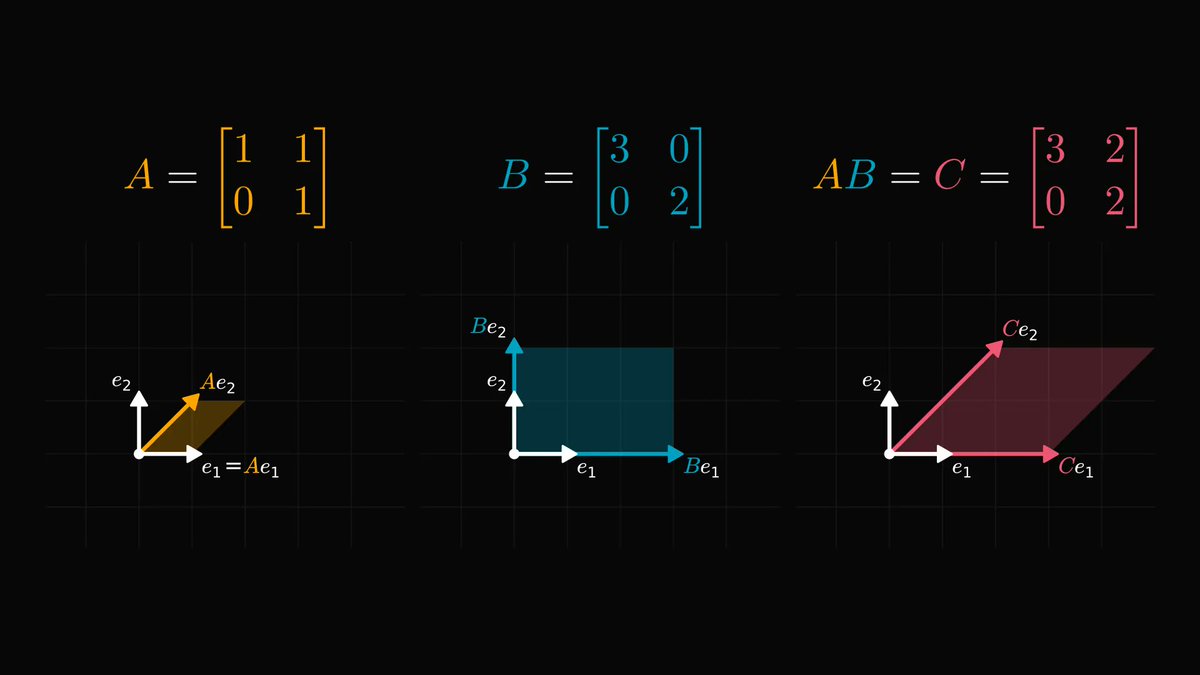Functions, the central objects of mathematics and computer science, are just mappings of inputs to outputs.

A convenient (albeit quite imprecise) way to define them is to describe their effect. An explicit formula is often available, which we can translate to code.

2/13

However, giving an explicit formula is not always easy or possible.

For instance, can you calculate the number of ways we can order a deck of n cards by shuffling its cards?

3/13

There is a solution besides giving a formula.

Suppose that we shuffled n-1 cards. Given a new one, we can insert it into the deck at n possible locations.

Thus, all the possible shuffles of n can be obtained by shuffling n-1 cards first, then inserting the remaining one.

4/13

Counting this way gives rise to a formula that references itself. This is called recursion.

For the computation to end, we have to supply a so-called boundary condition. In our case, this is simple: a "deck" consisting of 1 card can be shuffled only one way.

5/13

Every recursion has two crucial components: the recursive step and the boundary condition.

6/13

In practice, we can simply implement recursive functions by calling the function in its definition. Most programming languages support this.

Frequently, recursion is an extremely convenient way to write clear and concise functions.

7/13

However, recursion is a double-edged sword.

Let's talk about a case where the recursive step involves referencing the function multiple times.

The famous Fibonacci numbers provide an example of this.

8/13

Just like previously, we can easily supply a recursive function to compute the n-th Fibonacci number.

Can you think of any potential issues?

9/13

For each call, the function calls itself two times. Those make an additional two calls individually, and so on.

This is how the recursive calls look for n = 4. (Each arrow represents a function call.)

10/13

As you probably figured, this can blow up really fast.

Essentially, computing F(n) this way involves an exponential number of calls to F.

11/13

Just out of curiosity, I have measured the time it takes to compute a few Fibonacci numbers with the recursive function.

F(40) took more than 30 seconds on my computer. I had no patience to wait out F(50).

So, recursion can be really slow.

12/13

TL;DR: a recursive function is one that references itself in its definition. They are powerful, but can be really slow.

Can you think of a better way to implement the computation of the Fibonacci numbers? Share your ideas below! (I can think of at least three.)

13/13