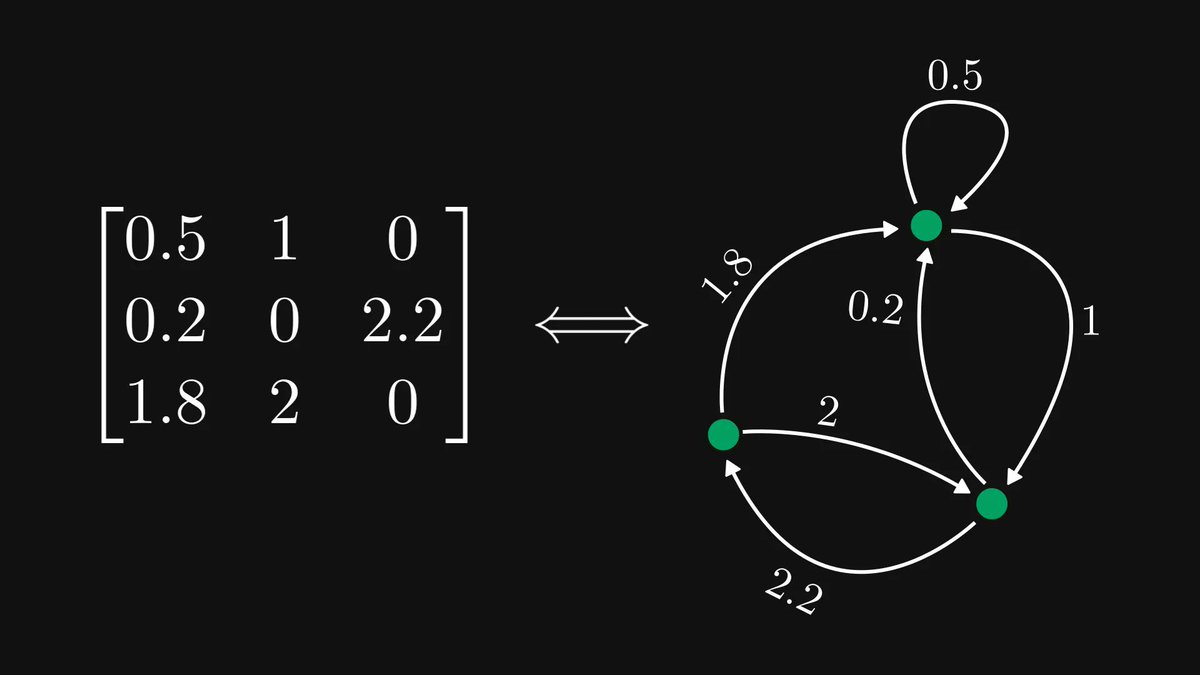
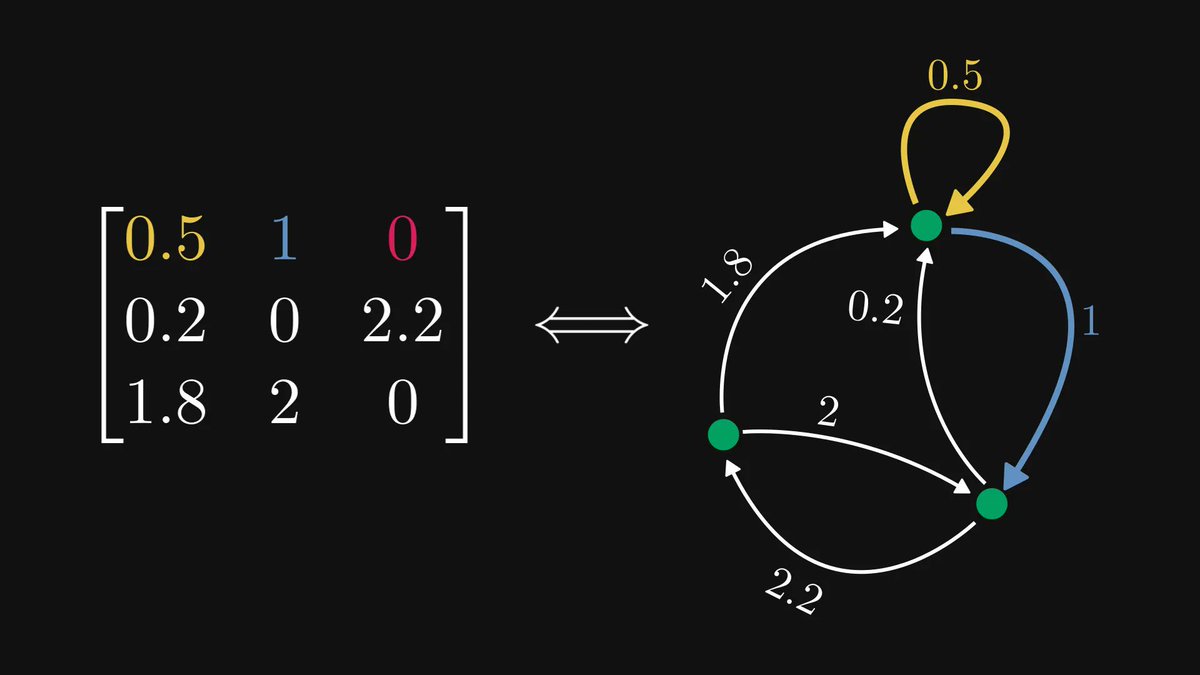
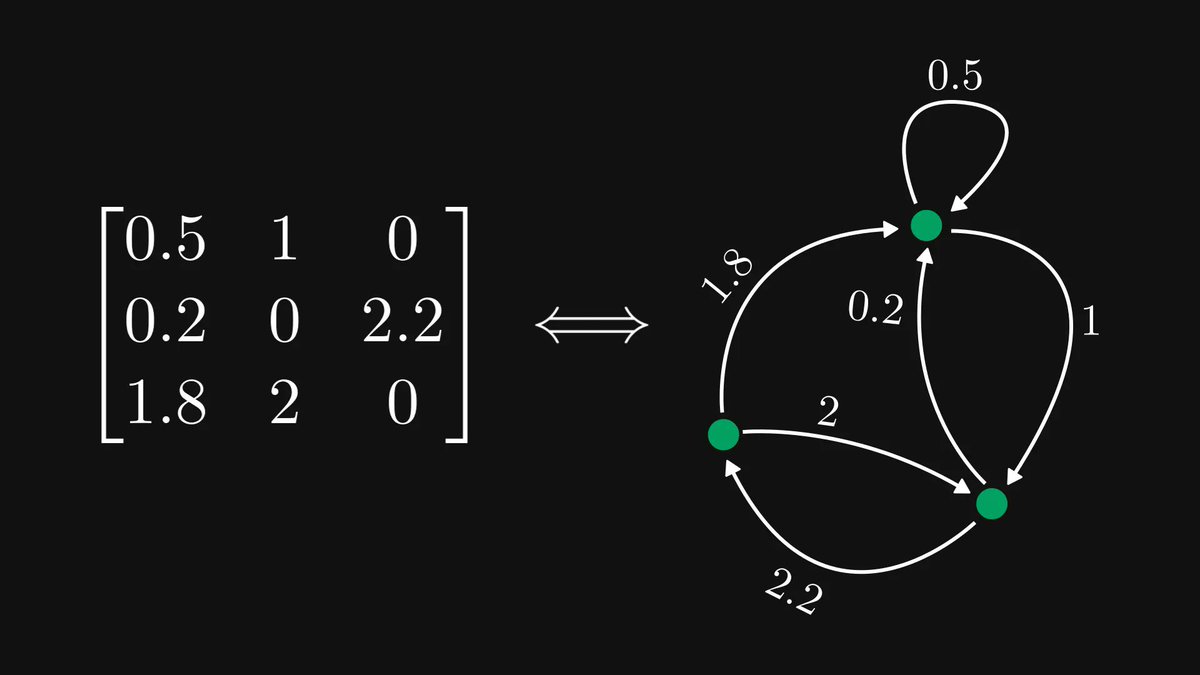
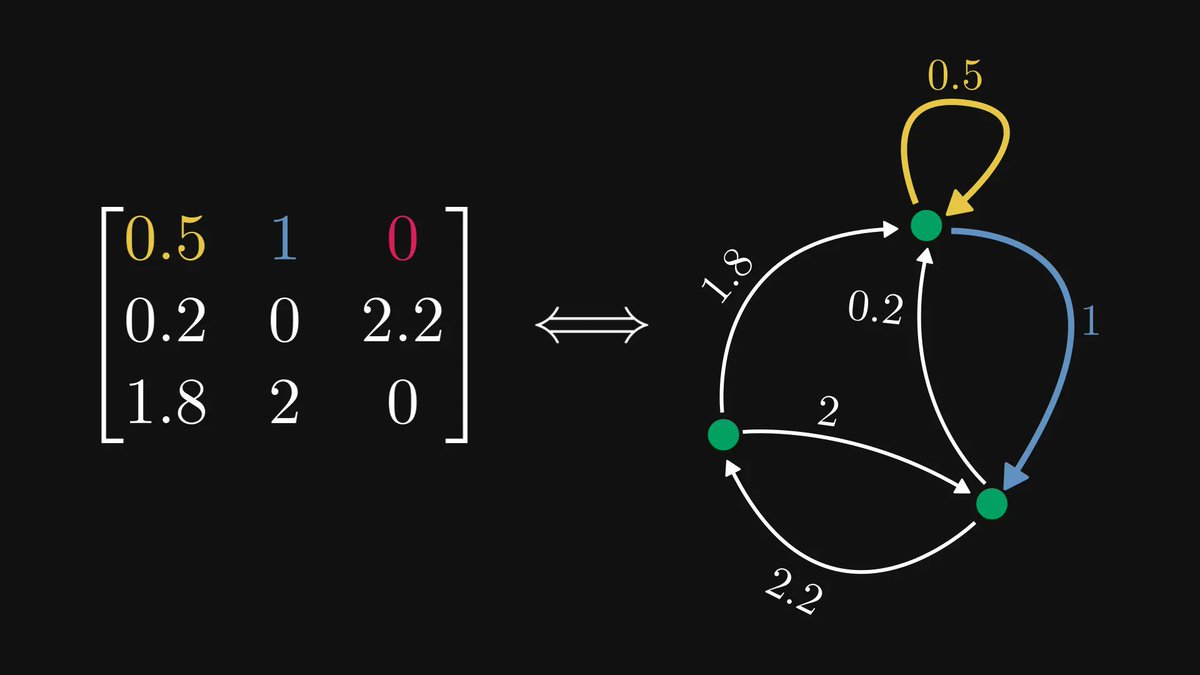
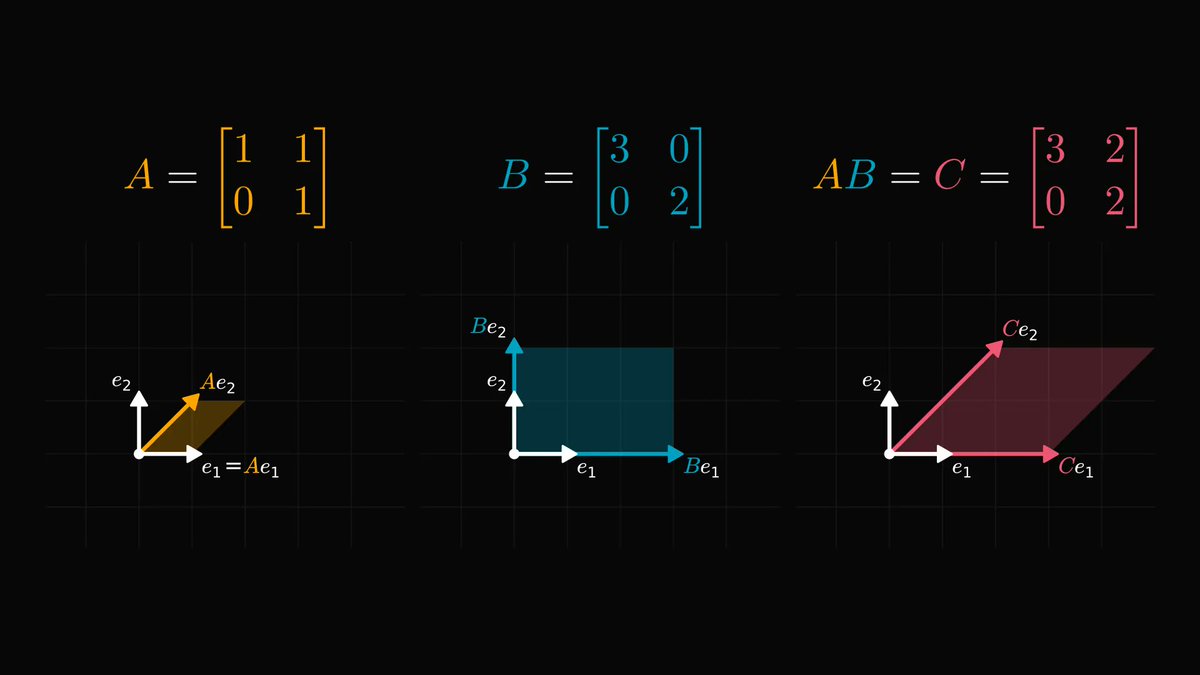Just released a new chapter in the early access of my Mathematics of Machine Learning book!
It is about computing determinants in practice. Sadly, this is often missing from linear algebra courses, so I decided to fill this gap.
↓ Here's the gist. ↓
It is about computing determinants in practice. Sadly, this is often missing from linear algebra courses, so I decided to fill this gap.
↓ Here's the gist. ↓
The determinant of a matrix is essentially the product of
• the orientation of its column vectors (which is either 1 or -1),
• and the area of the parallelepiped determined by them.
For 2x2 matrices, this is illustrated below.
• the orientation of its column vectors (which is either 1 or -1),
• and the area of the parallelepiped determined by them.
For 2x2 matrices, this is illustrated below.

Here is the thing.
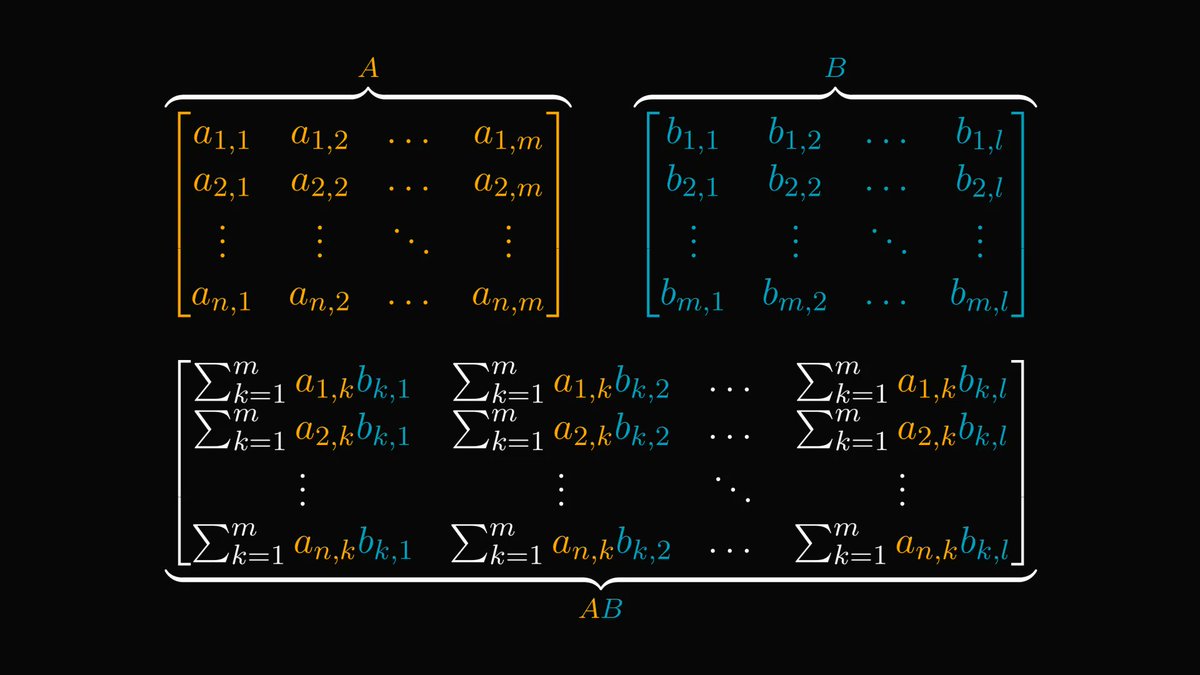
In mathematics, we generally use two formulas to compute this quantity.
First, we have a sum that runs through all permutations of the columns.
This formula is hard to understand, let alone to implement.
In mathematics, we generally use two formulas to compute this quantity.
First, we have a sum that runs through all permutations of the columns.
This formula is hard to understand, let alone to implement.

The other one is not so good either.
It is a recursive formula, so implementing it is not that hard, but its performance is horrible.
Its complexity is O(n!), which is unfeasible in practice.
It is a recursive formula, so implementing it is not that hard, but its performance is horrible.
Its complexity is O(n!), which is unfeasible in practice.

However, it takes almost 30 seconds to calculate the determinant of a 10 x 10 matrix.
This is not going to cut it.
This is not going to cut it.

With a little trick, we can simplify this problem a lot.
If the determinant is not zero, we can factor any A into the product of a lower and an upper triangular matrix. This is called the LU decomposition.
As a bonus, the diagonal of L is constant 1.
If the determinant is not zero, we can factor any A into the product of a lower and an upper triangular matrix. This is called the LU decomposition.
As a bonus, the diagonal of L is constant 1.

The LU decomposition takes O(n³) steps to compute, and the determinant of A can be easily read out from it: determinants of triangular matrices equal to the product of the diagonal elements. 

So, instead of O(n!), we can calculate determinants at O(n³) time.
The difference is stunning. With the recursive formula, a 10 x 10 determinant took 30 seconds. Using LU decomposition, we can do a 10000 x 10000 one in that time.
A bit of linear algebra can take us very far.
The difference is stunning. With the recursive formula, a 10 x 10 determinant took 30 seconds. Using LU decomposition, we can do a 10000 x 10000 one in that time.
A bit of linear algebra can take us very far.
Having a deep understanding of mathematics will make you a better engineer. This is what I want to help you with.
If you are interested in the details and the beauties of linear algebra, check out the early access for my book!
tivadar.gumroad.com/l/mathematics-…
If you are interested in the details and the beauties of linear algebra, check out the early access for my book!
tivadar.gumroad.com/l/mathematics-…
• • •
Missing some Tweet in this thread? You can try to
force a refresh