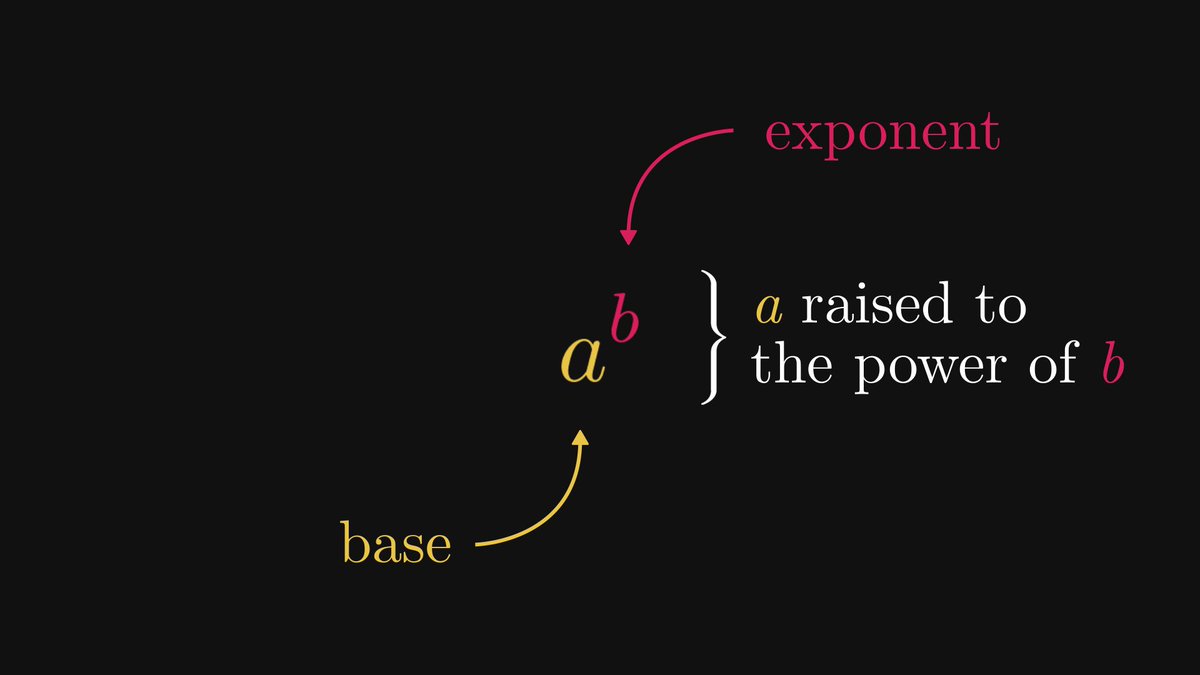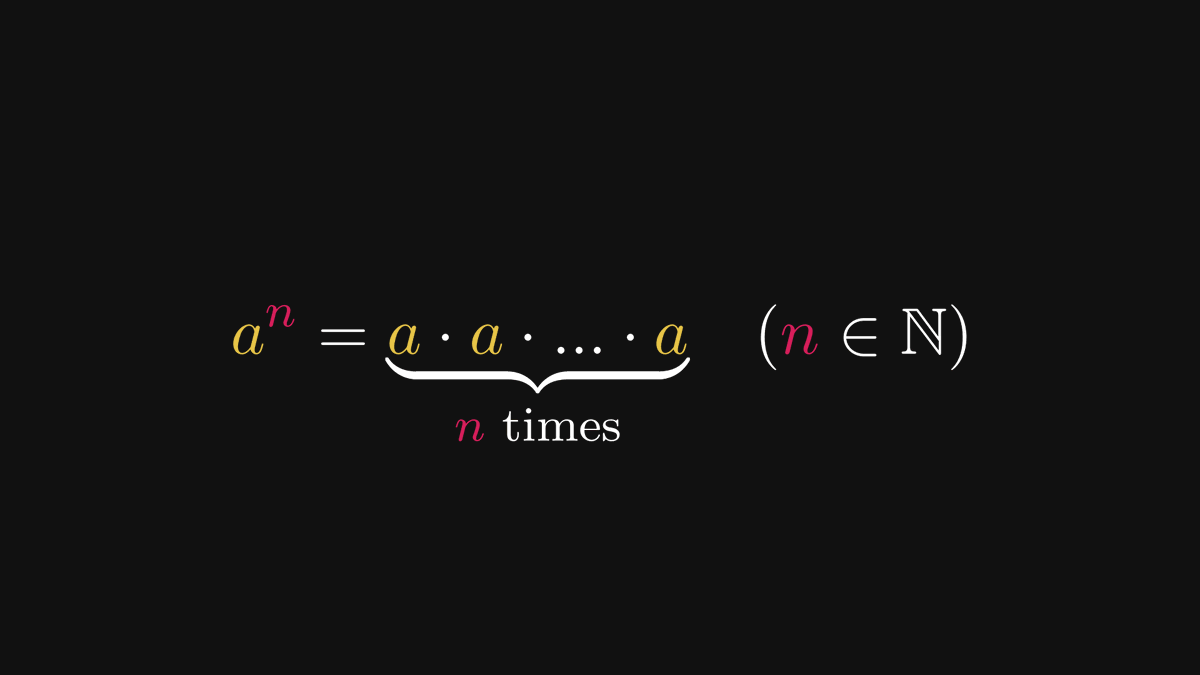Entropy is not the easiest thing to understand.
It is rumored to describe something about information and disorder, but it is unclear why.
What do logarithms and sums have to do with the concept of information?
Let me explain!
↓ A thread. ↓
It is rumored to describe something about information and disorder, but it is unclear why.
What do logarithms and sums have to do with the concept of information?
Let me explain!
↓ A thread. ↓

I have randomly selected an integer between 0 and 31.
Can you guess which one? You can ask as many questions as you want.
What is the minimum number of questions you have to ask to be 100% sure?
You can start guessing the numbers one by one, sure. But there is a better way!
Can you guess which one? You can ask as many questions as you want.
What is the minimum number of questions you have to ask to be 100% sure?
You can start guessing the numbers one by one, sure. But there is a better way!
If you ask, "is the number larger or equal than 16?" you immediately eliminate half the search space!
Continuing with this tactic, you can find the number for sure in 5 questions.
Continuing with this tactic, you can find the number for sure in 5 questions.
In other words, we need to take the base two logarithm of 32 to get the number of questions required.
This logic applies to all numbers! If I pick a number between 0 and 𝑛-1, you need 𝑙𝑜𝑔(2, 𝑛) questions to find it for sure, by cutting the possibilities in half with each.
This logic applies to all numbers! If I pick a number between 0 and 𝑛-1, you need 𝑙𝑜𝑔(2, 𝑛) questions to find it for sure, by cutting the possibilities in half with each.
Because the answers are yes-or-no questions, we can encode each with a 0 or 1.
If we write down the answers in a row, we effectively encode the numbers in 𝑛 bits!
𝟎: 00000
𝟏: 00001
𝟐: 00010
...
𝟑𝟏: 11111
Each "code" is simply the number in base 2!
If we write down the answers in a row, we effectively encode the numbers in 𝑛 bits!
𝟎: 00000
𝟏: 00001
𝟐: 00010
...
𝟑𝟏: 11111
Each "code" is simply the number in base 2!
No matter which number I pick, five questions are needed to find it.
So, the average number of bits needed is also five.
However, we use a critical assumption here: I pick each number with an equal probability.
What if that is not the case?
So, the average number of bits needed is also five.
However, we use a critical assumption here: I pick each number with an equal probability.
What if that is not the case?
Let's say I am picking between 0, 1, and 2, but I am picking 0 at 50% of the time, while 1 and 2 only 25% of the time.
We should put this into mathematical form!
Let's denote the number I pick with 𝑋. This is a random variable.
How many bits do we need now?
We should put this into mathematical form!
Let's denote the number I pick with 𝑋. This is a random variable.
How many bits do we need now?

We can be more bit-efficient than before! Consider this.
1st question: did you pick 0?
If the answer is yes, the 2nd question is not needed. If not, we proceed!
2nd question: did you pick 1?
No matter what the answer is, we know the solution! Yes implies 1, no implies 2.
1st question: did you pick 0?
If the answer is yes, the 2nd question is not needed. If not, we proceed!
2nd question: did you pick 1?
No matter what the answer is, we know the solution! Yes implies 1, no implies 2.
(This is just the expected value of the number of bits.
If you didn't understand this step, check out my explanation about the expected value!)
If you didn't understand this step, check out my explanation about the expected value!)
https://twitter.com/TivadarDanka/status/1471113068100800523)
Now we are almost there! Let's see the general case.
Suppose I pick between 𝑥₁, 𝑥₂, ..., 𝑥ₙ, and I pick 𝑥ₖ with probability 𝑝ₖ.
As before, the number of questions needed to find 𝑘 is the base two logarithm of 1/𝑝ₖ!
Suppose I pick between 𝑥₁, 𝑥₂, ..., 𝑥ₙ, and I pick 𝑥ₖ with probability 𝑝ₖ.
As before, the number of questions needed to find 𝑘 is the base two logarithm of 1/𝑝ₖ!

So, the entropy of a random variable is simply the average bits of information needed to guess its value successfully! Even though the formula is complicated, its meaning is simple.
Entropy is simpler than you thought! (And probably also simpler than what you were taught.)
Entropy is simpler than you thought! (And probably also simpler than what you were taught.)

Having a deep understanding of math will make you a better engineer. I want to help you with this, so I am writing a comprehensive book about the subject.
If you are interested in the details and beauties of mathematics, check out the early access!
tivadardanka.com/book
If you are interested in the details and beauties of mathematics, check out the early access!
tivadardanka.com/book
A few extra comments!
1. What happens if the logarithm of the probability is not an integer?
Not all questions provide 100% new information. Sometimes, the answer is partially contained in other bits.
Hence, the "amount of new information" is not always an integer.
1. What happens if the logarithm of the probability is not an integer?
Not all questions provide 100% new information. Sometimes, the answer is partially contained in other bits.
Hence, the "amount of new information" is not always an integer.
2. Does the base of the logarithm matter?
In general, we can easily swap the base of the logarithms, as shown below.
Thus, swapping bases in the entropy formula is just multiplication with a constant.
In general, we can easily swap the base of the logarithms, as shown below.
Thus, swapping bases in the entropy formula is just multiplication with a constant.

• • •
Missing some Tweet in this thread? You can try to
force a refresh