Thread by @VisualAlgebra

Happy New Year #MathTwitter! Let's start 2022 w/ Part 1 of a fun series: "Groups you Never Knew Existed...and others you can't POSSIBLY live without!"

Today we'll see the "diquaternions", a term you've never heard of b/c I made it up last month. Let's dig in! 🧵👇

1/17

We'll start with the familiar quaternion group Q_8. Shown here are several Cayley diagrams, a Cayley table, cycle diagram, subgroup lattice, its partition by conjugacy classes, and an action diagram of Aut(Q_8). Each of these highlights different structural features.

2/17

Next, have you ever wondered what would happen if you replace i=e^{2\pi i/4} in Q_8 with a larger root of unity?

These are the dicyclic groups. Here is Dic_6, for n=6. Note that n=4 gives Q_8.

The last two pictures highlight the orbit structure (cyclic subgroups).

3/17

The quotient Dic_n / <-1> is always dihedral. Here are several ways to see that.

Even though these groups generalize Q_8, when n is a power of two, Dic_n is called a "Generalized Quaternion Group", because it shares properties with Q_8 that other dicyclic groups don't.

4/17

In particular, "gen. quaternion groups" never break up as a semi-direct product of any proper subgroups, because every non-trivial subgroup contains -1. So no two can intersect trivially.

Here are the subgroup lattices of Q_{32}, Q_{16}, and Q_8. Compare to Dic_6, above.

5/17

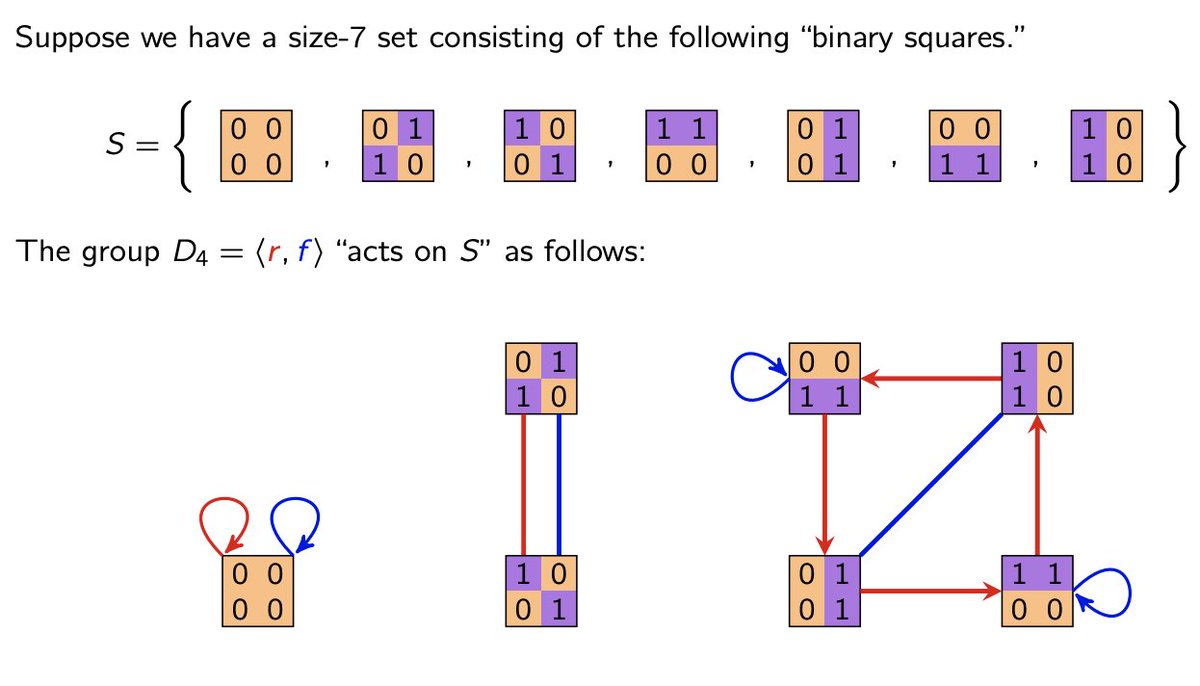
Now, let's talk 2x2 representations of these groups.

There is a canonical way (see images) to represent

D_n = <r, f> = <R_n, F>, and
Q_8 = <i, j> = <R_4, S>.

Here: R_n = "rotation", F = "flip", and S = "j".

Put these together to get

Dic_n = <r, j> = <R_n, S>!

6/17

So, dicyclic groups are what we get by replacing R_4 with R_n in Q_8.

But there's something else we can do: start with the QUATERNION group Q_8 and add the *reflection* matrix F from the DIHEDRAL group D_n!

This defines the "DIQUATERNION group", DQ_8.

7/17

You've never heard the term "diquaternion" because I coined it 2 weeks ago. It consists of the matrices

DQ_8 = { ±I, ±X, ±Y, ±Z, ±iI, ±iX, ±iY, ±iZ},

where X, Y, Z are the "Pauli matrices" from quantum physics.

This is also called the "Pauli group on 1 qubit".

8/17

Fun exercise, good for students: show that the quotient DQ_8 / <-I> is Z2^3, by making a Cayley table with the following 8 entries:

±I, ±X, ±Y, ±Z, ±iI, ±iX, ±iY, ±iZ,

like we did with Q_8 and Dic_6 in tweets 2 & 4.

Show that it has the structure of this.

9/17

Another fun exercise for your algebra students:

Label the following cycle diagram with elements from the diquaternion group DQ_8. This will help see different aspects of its structure. It has 4 max'l orbits of size-4, and 5 of size 2.

10/17

Purely visually, we can find three index-2 subgroups H of DQ_8, isomorphic to

D_4 (the outer ring)
Q_8 (yellow nodes)
C4 x C2 (nodes along the x & y axes).

Another fun exercise for your students: for which of these H does DQ_8 ≅ H ⋊ C2?

11/17

Do you see what's coming next? What if we replace "R_4" in the rep. for DQ_8 with a different rotation R_n, like we did to generalize Q_8 --> Dic_n.

For n=2^k, this defines the "Generalized Diquaternion Group". Here is DQ_{16}.

12/17

There are Pauli groups on n qubits, formed by tensoring, but these have order 4^{n+1}. So the first 4 have sizes 16, 64, 256, 1024. In contrast, there's a diquaternion group for every power of 2 bigger than 8.

13/17

These groups belong in any ugrad algebra class! It's skipped b/c without visuals, it really hard to motivate. Who *really* understands it from the following presentation:

<a,b,c | a^4 = c^2 = 1, a^2 = b^2, ac=ca, a^2b=cba>

Even the fantastic website "WeddsList"...

14/17

...hosted by N.S. Wedd says

"among the groups of order less than 32, the Pauli group is one of the hardest to understand"

weddslist.com/groups/cayley-…

But now you've seen how to do it naturally!

15/17

If you want to use graphics like this in your next algebra class, get in touch! There is so much more milage you get by doing things visually, and it really hammers home the inherent BEAUTY in math, that your students will never forget!

And I promise, it's SO MUCH FUN!

16/17

I've got lots of materials to share. I'm also finishing a ~600 page book, that I'm hoping will completely change how algebra is taught. My materials (slides, HW, videos) will always be freely available. But there's no going back!

Here's to a great 2022, Happy Near Year!

17/17

UPDATE & CORRECTION: On #10/17, I had a blank cycle diagram that was for the wrong group, V4⋊C4. It has the same # of elts of each order as DQ_8, but is not isomorphic.

I just made these diagrams. 2 different ways to label DQ_8: one w/ Pauli matrices, and the other...

18/17

...with the elements of <R,S,F>, where Q_8=<R,S> and D_n = <R_n, F>.

Here are their cycle diagrams w/ the same labelings. The yellow nodes highlight the subgroup Q_8.

I found this informative, it's something I simply had never done until just now. Hope you enjoy!

19/17