
Associate Professor (Clemson) | AIMS Lecturer (South Africa) | Author: "Visual Algebra" (forthcoming) | YouTuber | First Gen | Homesteader | Dad to Ida & Felix
5 subscribers
How to get URL link on X (Twitter) App


 If G acts on S, via ϕ:G→Perm(S), imagine that G has a "group switchboard", w/ a button for each element. Pressing it permutes elements of S, with the rule:
If G acts on S, via ϕ:G→Perm(S), imagine that G has a "group switchboard", w/ a button for each element. Pressing it permutes elements of S, with the rule:

 We started #Week1 of #VisualAlgebra with a few quotes from "A Mathematician's Apology" on the beauty of mathematics, and then saw Cayley diagrams for the symmetries of the rectangle and triangle.
We started #Week1 of #VisualAlgebra with a few quotes from "A Mathematician's Apology" on the beauty of mathematics, and then saw Cayley diagrams for the symmetries of the rectangle and triangle.https://twitter.com/VisualAlgebra/status/1482065699212120064
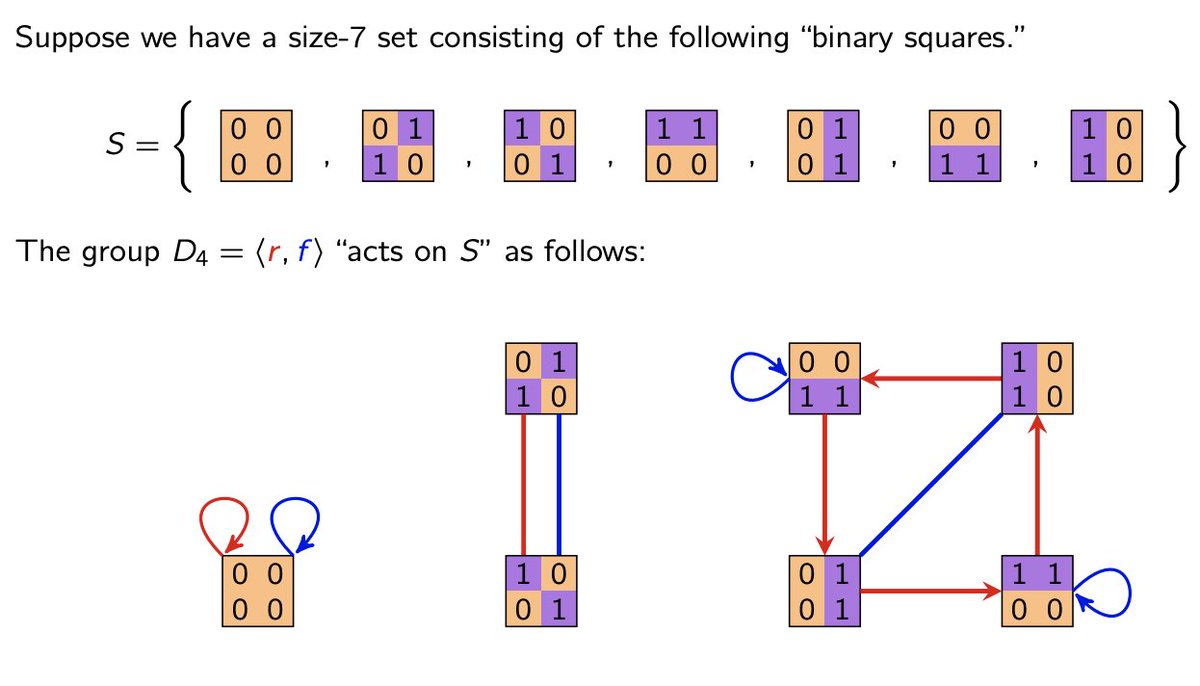
 See those "orbit diagrams" above? I got to thinking: "how can we characterize all possible diagrams?" Equivalently, all transitive actions of D_4 (or a group G in general).
See those "orbit diagrams" above? I got to thinking: "how can we characterize all possible diagrams?" Equivalently, all transitive actions of D_4 (or a group G in general).


 The integers have nice properties that we usually take for granted:
The integers have nice properties that we usually take for granted: 
 Though we constructed semidirect products visually last week, we haven't yet seen the algebraic definition. On Friday, we saw inner automorphisms, which was the last step we needed.
Though we constructed semidirect products visually last week, we haven't yet seen the algebraic definition. On Friday, we saw inner automorphisms, which was the last step we needed. 



 Pause for a quick comment about cosets in additive groups. Don't forget to write a+H, rather than aH. Here's a nice way to see the equality of a left coset and a right coset.
Pause for a quick comment about cosets in additive groups. Don't forget to write a+H, rather than aH. Here's a nice way to see the equality of a left coset and a right coset.



 We learned some neat facts about the Rubik's cube, like how the group has just 6 generators, but 4.3 x 10^{19} elements, and a Cayley diagram with diameter of 20 or 26, depending on whether you count a 180 degree twists as 1 or 2 moves.
We learned some neat facts about the Rubik's cube, like how the group has just 6 generators, but 4.3 x 10^{19} elements, and a Cayley diagram with diameter of 20 or 26, depending on whether you count a 180 degree twists as 1 or 2 moves.

 We have not yet defined a group. Rather, we are exploring the intuition of them via symmetries. This will *motivate the axioms*, rather than the other way around.
We have not yet defined a group. Rather, we are exploring the intuition of them via symmetries. This will *motivate the axioms*, rather than the other way around. 

 We'll start with the familiar quaternion group Q_8. Shown here are several Cayley diagrams, a Cayley table, cycle diagram, subgroup lattice, its partition by conjugacy classes, and an action diagram of Aut(Q_8). Each of these highlights different structural features.
We'll start with the familiar quaternion group Q_8. Shown here are several Cayley diagrams, a Cayley table, cycle diagram, subgroup lattice, its partition by conjugacy classes, and an action diagram of Aut(Q_8). Each of these highlights different structural features. 




 First, I'm wasn't at all picking on anyone, but rather, at how this concept (and so many others) are taught in nearly every algebra class and book.
First, I'm wasn't at all picking on anyone, but rather, at how this concept (and so many others) are taught in nearly every algebra class and book.


 The key lemma needed for the Sylow theorems is:
The key lemma needed for the Sylow theorems is: 