Tweet

AkaSci CU@L2

9 Jan, 5 tweets, 4 min read

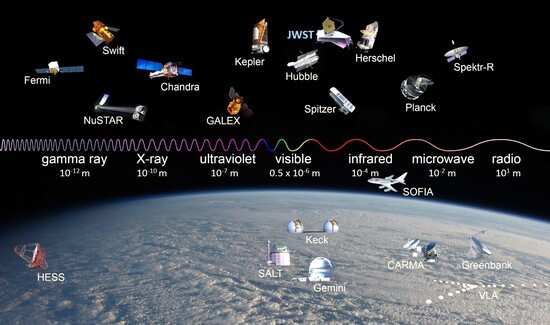
Where does #JWST reside on the spectrum of telescopes? The EM spectrum ranges for various space-based telescopes and a few ground telescopes are shown below. JWST observes in the 0.6–28.3 μm wavelength range (orange to mid-infrared). Hubble ST observes in the 0.1–1.0 μm range.

The Herschel Space Observatory, active from 2009 to 2013, observed in the far IR 55-672 µm range, from its perch at L2 (same as #JWST!). Its 3.5 m mirror was made of sintered silicon carbide. Detectors were kept at temps below 2 deg K, using 2,300 litres of liquid helium at 1.4 K

The Spitzer Space Telescope, 2003-2020, observed in the infrared 3.6-160 µm range from an Earth-trailing orbit. Its 0.85 m Beryllium mirror and detectors were kept at near zero temps using liquid helium. The LHE depleted in 2009, limiting Spitzer to shorter wavelengths.

Sources for above tweets #JWST #HST #Herschel #Spitzer -
imagine.gsfc.nasa.gov/Images/science…
en.wikipedia.org/wiki/James_Web…
en.wikipedia.org/wiki/Hubble_Sp…
en.wikipedia.org/wiki/Herschel_…
en.wikipedia.org/wiki/Spitzer_S…

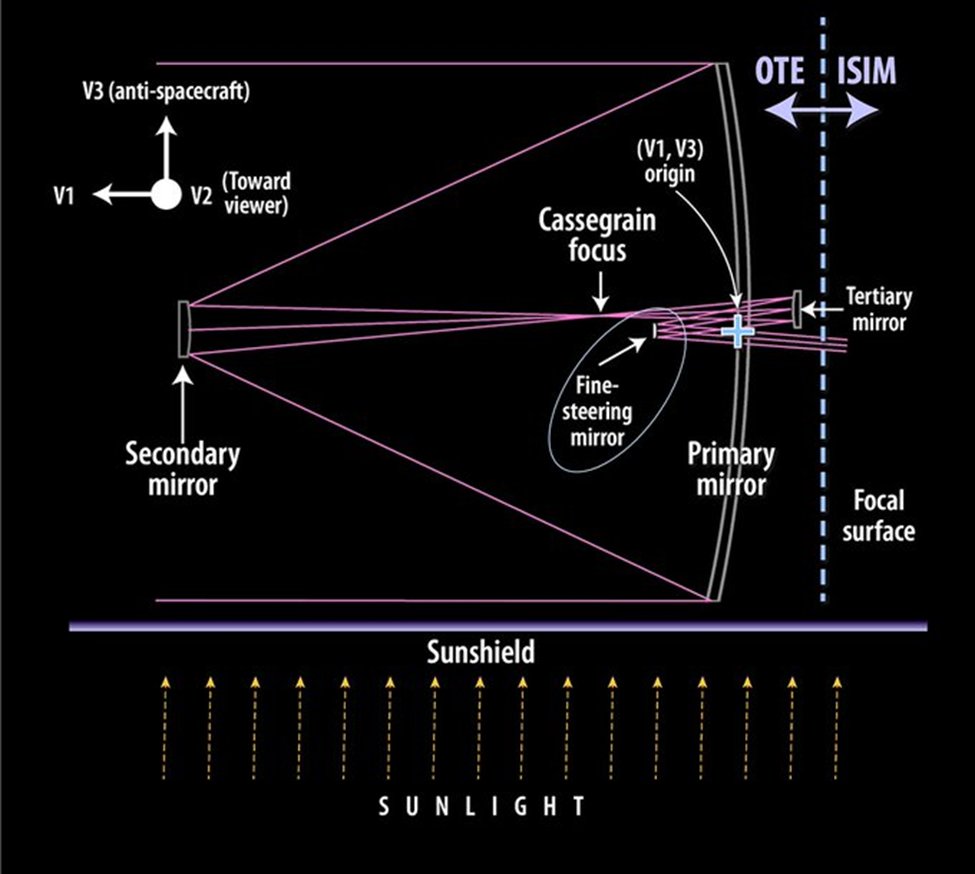
Fun fact - JWST's secondary mirror at 0.74 m is almost as large as Spitzer's primary mirror at 0.85 m. But, #JWST mirror temp of 50 K cannot match the 5.5 K temp of Spitzer's mirrors, since it uses passive cooling, not liquid He. That is likely why spectrum coverage is different.

• • •

Missing some Tweet in this thread? You can try to force a refresh

This Thread may be Removed Anytime!

Twitter may remove this content at anytime! Save it as PDF for later use!

More from @akaschs

AkaSci CU@L2

@akaschs

11 Jan

While we wait 6 months for #JWST to get ready, let's explore what sorts of images and data we can expect from JWST.
We are all used to seeing Hubble's dazzling images of galaxies and nebulae. Will JWST's images look like these?
1/

Hubble primarily observes in the UV and visible light wavelengths from 0.1-0.8 μm but it can also see parts of the infrared (IR) spectrum from 0.6-2.5 μm.
Visible light images can produce the colorful ghostly images of nebulae but IR can reveal more distant stars and galaxies.
2/

Can we can expect #JWST images to be similar to those on the right above? JWST observes in the orange to mid-infrared wavelengths from 0.6-28.3 μm.
JWST’s NIRCam and NIRSpec instruments cover 0.6 to 5 μm, the MIRI ultra-cold instrument covers 5 to 27 μm
Can JWST see farther?
3/

Read 18 tweets

AkaSci CU@L2

@akaschs

8 Jan

Here is a simple approximate method to compute the distance of the Lagrange L2 point from Earth.
An object at L2 is orbiting around the Sun at the same period as earth, i.e., 365.25 days. Let’s assume a circular orbit, centered at the Sun.

At L2, the centrifugal force on the object due its orbital motion must balance out the gravitational forces of earth and the Sun on the object.
i.e., Fsun + Fearth = Fc
Using the notations from the diagram, we have
Fsun = G * Ms * m / (R + r)^2 (Newton’s equation)

Fearth = G * Me * m / r^2
Fc = m * w^2 * (R + r) (w (omega) is the angular speed of object in radians/s)
Hence, we get
G * Ms * m / (R + r)^2 + G * Me * m / r^2 = m * w^2 * (R + r)
Removing m, we get –
G * Ms / (R + r)^2 + G * Me / r^2 = w^2 * (R + r)

Read 6 tweets

AkaSci CU@L2

@akaschs

7 Jan

Let’s take a look at JWST mirrors.
Besides the familiar large primary mirror, JWST contains 3 other mirrors – a secondary mirror mounted at the end of the tripod struct, a tertiary mirror and a fine steering mirror. The figure below shows the path of IR light across the mirrors.

We all know that the JWST primary mirror is composed of 18 hexagonal mirror segments.
Each mirror segment is 1.3 meters from side-to-side, 2 inches thick and weighs 40 kg.

The mirror is made of Beryllium, atomic number = 4, a stiff and light-weight metal, 4.2 times lighter than steel, a good conductor of electricity and heat and excellent at holding its shape across a wide range of temperatures.

Read 24 tweets

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Too expensive? Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal

Or Donate anonymously using crypto!

Ethereum

0xfe58350B80634f60Fa6Dc149a72b4DFbc17D341E copy

Bitcoin

3ATGMxNzCUFzxpMCHL5sWSt4DVtS8UqXpi copy

Thank you for your support!

Share this page!

AkaSci CU@L2

Try unrolling a thread yourself!

More from @akaschs

AkaSci CU@L2

AkaSci CU@L2

AkaSci CU@L2

Did Thread Reader help you today?

Like this author's thread?