WEEK 1: first lecture of #VisualAlgebra.
"The mathematician's patterns, like the painter's or the poet's must be beautiful; the ideas like the colours or the words, must fit together in a harmonious way."
― G.H. Hardy, A Mathematician's Apology
1/4
"The mathematician's patterns, like the painter's or the poet's must be beautiful; the ideas like the colours or the words, must fit together in a harmonious way."
― G.H. Hardy, A Mathematician's Apology
1/4

We have not yet defined a group. Rather, we are exploring the intuition of them via symmetries. This will *motivate the axioms*, rather than the other way around.
What properties does this group have what might not hold more generally?
2/4
What properties does this group have what might not hold more generally?
2/4

For further insight, consider the symmetries of a triangle. This motivates the idea of relations, and why this "group calculator" tool is useful.
I got so many really good questions and comments in class today. How often does that happen on *Day 1* of abstract algebra??
3/4
I got so many really good questions and comments in class today. How often does that happen on *Day 1* of abstract algebra??
3/4

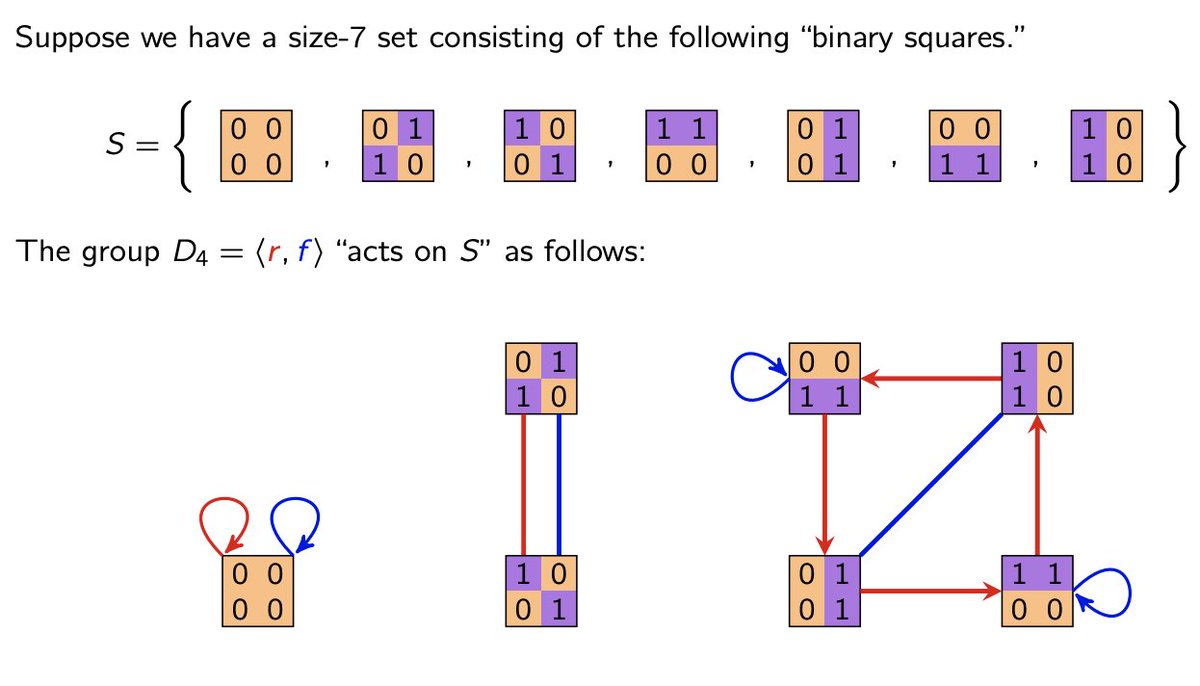
Finally, we ended with a Cayley diagram using a different set of generators. (Henceforth, bi-directed arrows will be un-directed).
From a distance, these don't look like the same group. But they are! Surprised? And that's a wrap!
Questions & comments welcome!
4/4
From a distance, these don't look like the same group. But they are! Surprised? And that's a wrap!
Questions & comments welcome!
4/4

• • •
Missing some Tweet in this thread? You can try to
force a refresh