WEEK 2 of #VisualAlgebra! This is only Lecture #2 of the class.
Monday was MLK Day, but on Wed, we learned about the Rubik's cube! I got to show up my rare signed cube with Ernő Rubik himself from 2010! Did a shout out to @cubes_art's amazing talents.
1/8 W


Monday was MLK Day, but on Wed, we learned about the Rubik's cube! I got to show up my rare signed cube with Ernő Rubik himself from 2010! Did a shout out to @cubes_art's amazing talents.
1/8 W


We learned some neat facts about the Rubik's cube, like how the group has just 6 generators, but 4.3 x 10^{19} elements, and a Cayley diagram with diameter of 20 or 26, depending on whether you count a 180 degree twists as 1 or 2 moves.
2/8 W
2/8 W

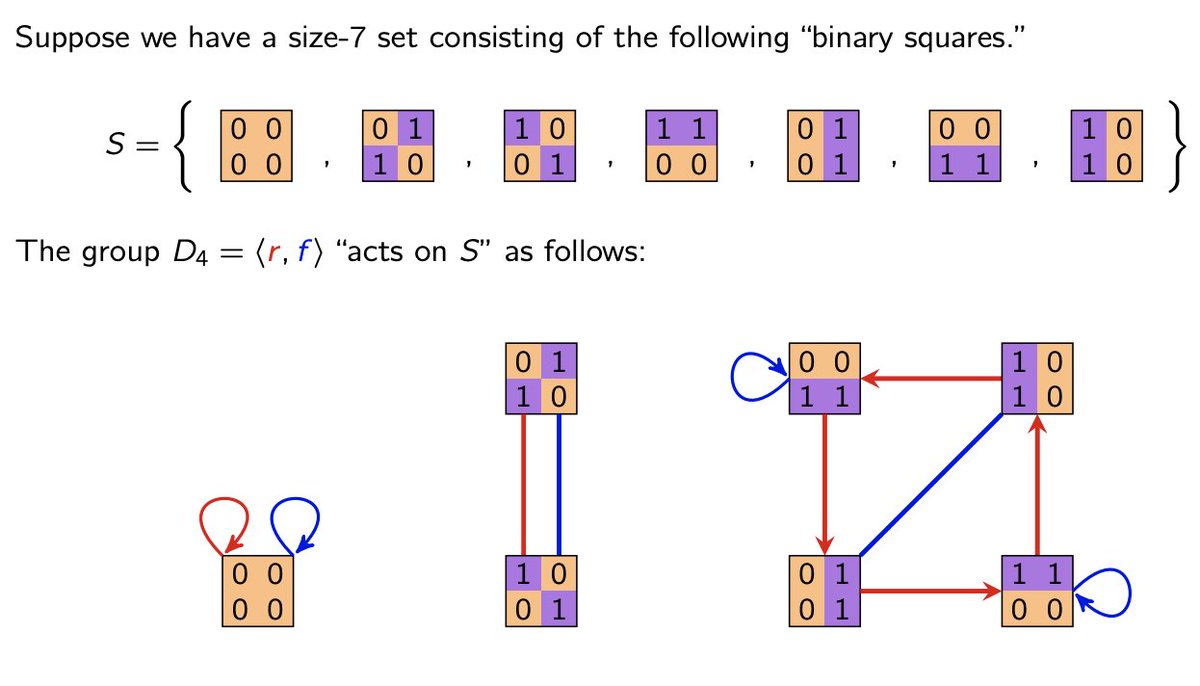
I showed 3 different groups of order 8, and asked if any are isomorphic. At this point, all they know about what that means is that two groups must have identical Cayley diagrams *for some generating set*.
3/8 W


3/8 W



But given two seemingly very different diagrams, how can we be *sure* that they aren't secretly isomorphic? How would a "yes certificate" differ from a "no certificate"? Like with these two pairs of examples.
These are fun things to ponder.
4/8 W

These are fun things to ponder.
4/8 W


We learned three different ways to display a Cayley diagram:
1. Label the nodes by configurations
2. Unlabeled nodes
3. Label the nodes by "actions" (many choices!)
This last choice makes a Cayley diagram into a "group calculator". Super convenient!
5/8 W

1. Label the nodes by configurations
2. Unlabeled nodes
3. Label the nodes by "actions" (many choices!)
This last choice makes a Cayley diagram into a "group calculator". Super convenient!
5/8 W


Finally, group presentations! This is an algebraic way to encode a Cayley diagram. Or equivalently, a Cayley diagram is a VISUAL REPRESENTATION of a presentation, and nothing more!
I asked them to imagine learning this material w/o the diagrams -- purely algebraically.
6/8 W
I asked them to imagine learning this material w/o the diagrams -- purely algebraically.
6/8 W
That idea just seemed so preposterous at this point.
Speaking of presentations, here's a fun tidbit / QUIZ that I posed! Consider the following 5 presentations of the group of symmetries of the triangle.
What group results if you remove r^3=1 from these 5 presentations?
7/8 W
Speaking of presentations, here's a fun tidbit / QUIZ that I posed! Consider the following 5 presentations of the group of symmetries of the triangle.
What group results if you remove r^3=1 from these 5 presentations?
7/8 W

Actually, it depends! The relation r^3=1 is implied by other relations in the first 2 presentations.
But removing it from the last 3 defines an infinite group.
Surprised? (I was when I learned this last fall!)
Stay tuned for Friday, when we learn what this group is!
8/8 W
But removing it from the last 3 defines an infinite group.
Surprised? (I was when I learned this last fall!)
Stay tuned for Friday, when we learn what this group is!
8/8 W

Today in #VisualAlgebra, we learned about frieze groups. There are 7 of these, and they are all subgroups of the frieze shown below. Notice how there is a concise way to describe each symmetry.
1/8 Fri



1/8 Fri




To find other frieze groups, let's force the vertical reflection 'v' to not be a symmetry. There are three ways we can do this.
Frieze 2: we lose the "odd reflections" and the "even rotations". Note that this was our "mystery group" from Wednesday! (see above)
2/8 F

Frieze 2: we lose the "odd reflections" and the "even rotations". Note that this was our "mystery group" from Wednesday! (see above)
2/8 F


Frieze 3: we keep all reflections but lose all 180-rotations.
Frieze 4: we keep all rotations but lose all reflections.
Note that these 3 groups (#2,3,4) are isomorphic!
3/8 F
Frieze 4: we keep all rotations but lose all reflections.
Note that these 3 groups (#2,3,4) are isomorphic!
3/8 F

Alternatively, if we take away all rotations & horizontal reflections, we get an abelian frieze group.
There are two more frieze groups, both cyclic.
4/8 F

There are two more frieze groups, both cyclic.
4/8 F


Let's make a Cayley diagram for that first frieze group we saw, using the motifs of our other friezes:
red = translation
orange = vertical flip (across horizon. axis)
blue = horizontal flip (across central vertical axis)
Exercise: label these nodes by symmetry type!
5/8 F
red = translation
orange = vertical flip (across horizon. axis)
blue = horizontal flip (across central vertical axis)
Exercise: label these nodes by symmetry type!
5/8 F

We also discussed the word problem for groups, which is undecidable. It relies on the fact (due to A. Turing) that the Halting Problem is undecidable. Which was a remarkable thing just to even formulate in the 1930s.
6/8 F

6/8 F


A halting checker could be used to resolve Russell's paradox.
A related problem in topology: start with the classification of 2D and 3D surfaces (PacMan analogies!), and pose the problem of whether a 4D surface is homeomorphic to the 4-sphere.
7/8 F
A related problem in topology: start with the classification of 2D and 3D surfaces (PacMan analogies!), and pose the problem of whether a 4D surface is homeomorphic to the 4-sphere.
7/8 F
4D space is "big enough" that for any G, we can build a surface S with fund. gp. π_1(G)≅S. So if we could solve this problem, we could use it to solve the word problem for an arbitrary group G.
This is a fun way to tie together algebra, CS, topology, and logic.
8/8 F
This is a fun way to tie together algebra, CS, topology, and logic.
8/8 F
• • •
Missing some Tweet in this thread? You can try to
force a refresh