Share this page!

Enter URL or ID to Unroll

You can paste full URL like: https://x.com/threadreaderapp/status/1644127596119195649
or just the ID like: 1644127596119195649

How to get URL link on X (Twitter) App

  1. On the Twitter thread, click on or icon on the bottom
  2. Click again on or Share Via icon
  3. Click on Copy Link to Tweet
  4. Paste it above and click "Unroll Thread"!
  5. More info at Twitter Help
Markku Kurtti Profile picture
@markku_kurtti
Jan 30, 2022 • 22 tweets • 7 min read • Read on X
Scrolly
1/
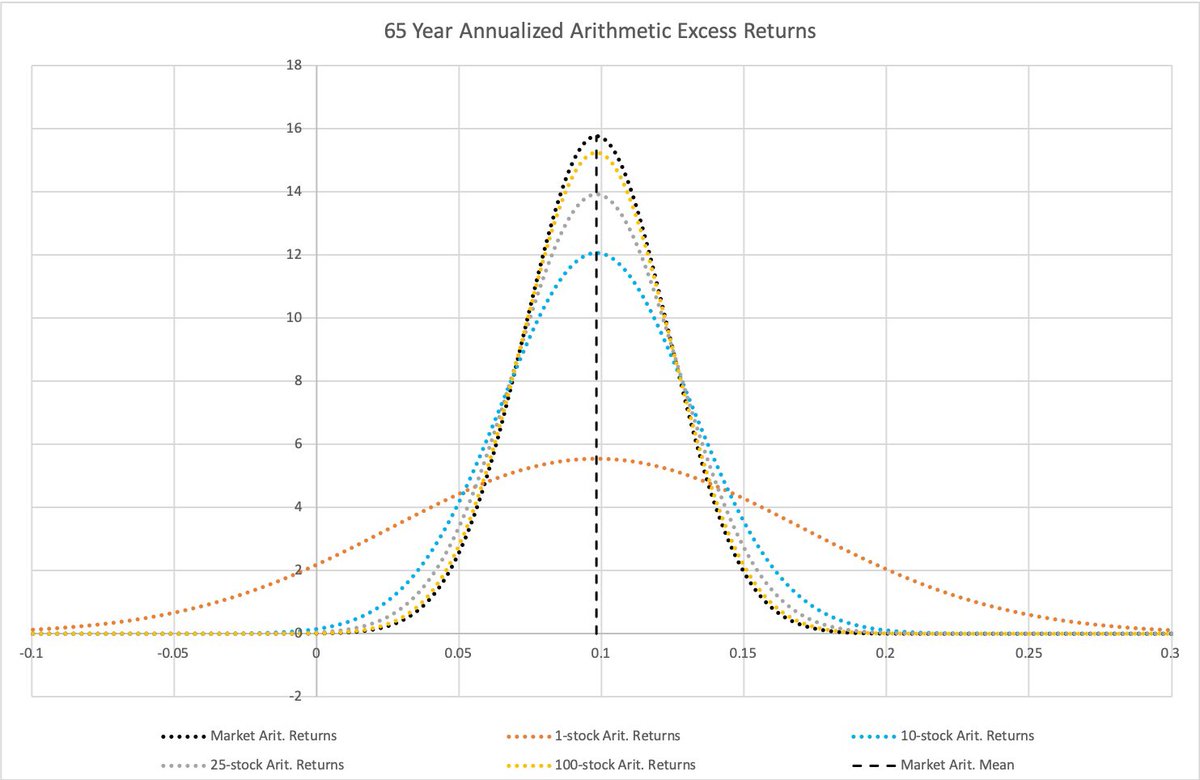
 Miten indeksiin sijoittava selvännäkijä määrittäisi sijoitusasteensa?

Selvännäkijällä on kyky nähdä tulevaisuuteen 10 vuoden periodille kaksi parametria: Sharpe ratio ja volatiliteetti, ei muuta. Näillä tiedoilla voidaan valita tuoton maksimoiva sijoitusaste.

#sijoittaminen
2/
 @hkeskiva ketju käteisen optioarvosta innosti tutkimaan mikä voisi olla sijoitusaseen optimi pitkällä aikavälillä.

Yritänkin myös tässä ketjussani tutkia CAPEn kykyä ennustaa optimaalinen sijoitusaste.

3/
 Lähtökohtani on Kelly-kriteerin hyödyntäminen.

Kelly-kriteerin mukaan geometrisella keskituotolla on maksimi ns. Full Kelly -sijoitusasteella, jonka jälkeen lisäriski johtaa pienevään tuotto-odotukseen.

Sijoitusasteen kasvattamisella on siis vähenevä rajahyöty.
4/
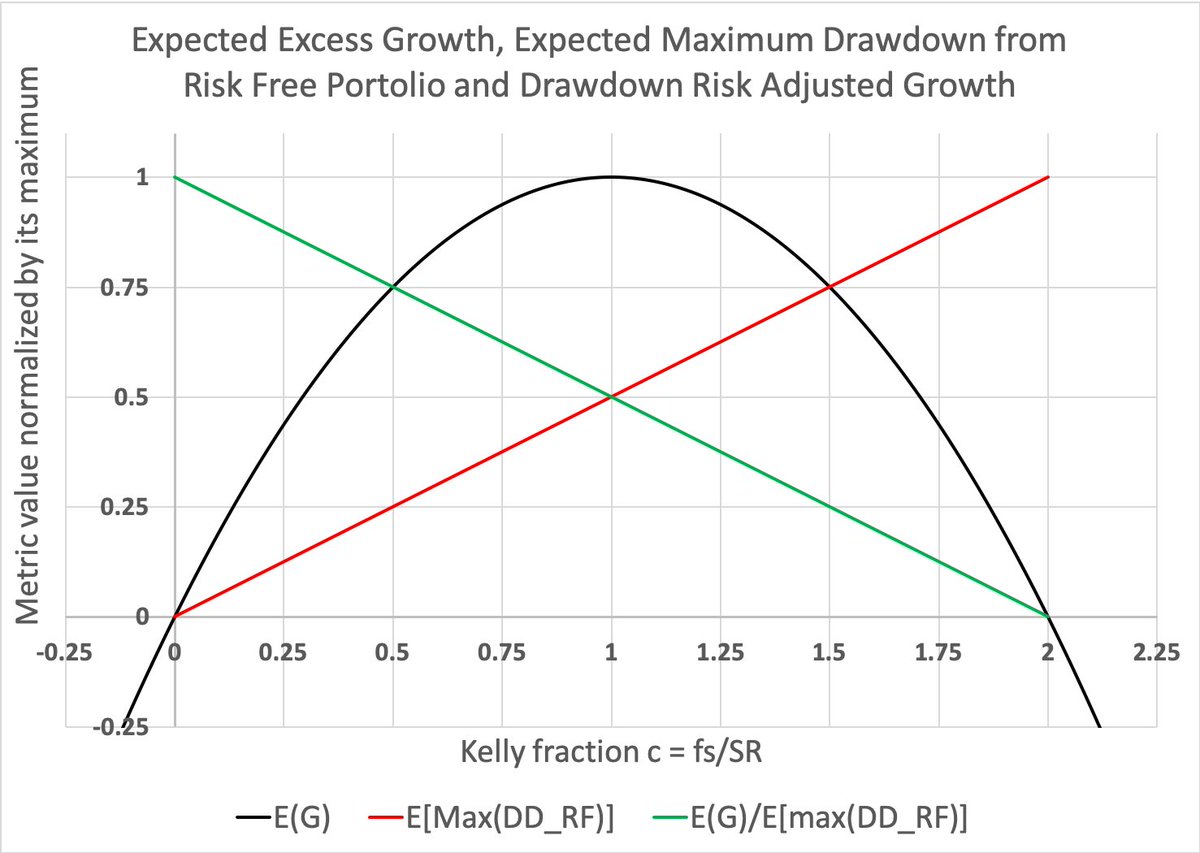
 Maksimi CAGR tuottavalla Full Kelly -sijoitusasteella Kelly fraktio c = 1.

Puolikkaalla Kelly fraktiolla c=0.5 saavutetaan 75% maksimituotosta, mutta vain 50% volatiliteetista.

c=2 sijoitusasteella tiputaan riskittömän koron tuotto-odotukseen ja siitä edelleen miinukselle.
5/
 Tuoton lisäksi sijoitusaste vaikuttaa riskiin.

Kelly fraktio yksinään määrittää sijoitushetken portfolion arvoon kohdistuvan maksimiarvonlaskuriskin (max-drawdown nykyarvosta) odotusarvon, joka on c/2 eli Full Kellyllä 50%.

Tarkemmin aiheesta: sijoitustieto.fi/sijoituskeskus…
6/
 Tarkastellaan (French data) U.S. kuukausituottoja Jul/1926 – Jun-2021.

Kuvasta näemme maksimi-CAGRia janoavan selvännäkijän sijoitusasteen ajan funktiona. Vaihteluväli on hurja: Min: -1.83 (Oct-1964), Max: 14.36 (Jun-1949).

Optimisijoitusasteen määrittää Sharpe/Vola.
7/
 Sijoitusaste seuraa Sharpen muotoa.

Sharpe seuraa aritmeettista riskittömän koron ylittävää keskituottoa, joka vaihtelee kovasti.

Volatiliteetin muutokset näyttävät rauhallisemmilta.

Tuotto-odotuksen ennustaminen näyttää oleelliselta sijoitusasteen valinnalle.
8/
 Kuten odotettua, optimisijoitusaste selvästi kasvaa aritmeettisen riskilisän (risk premium eli excess returnin keskiarvo) funktiona. Mutta muoto ei ole nätti suora vaan jokseenkin erikoinen viuhka.
9/
 Mistä moinen muoto?

CAGRn maksimoivaan sijoitusasteeseen vaikuttaa vain Sharpe ja vola. Sharpe itsessään koostuu mean excess returnista ja volasta, jolloin meille jää vain yksi selitys: Volatiliteetti.
10/
 Entäpä saavutettavissa oleva maksimi-CAGR eli CAGR-kapasiteetti?

Sama juttu: tuotto-odotus on oleellinen, mutta huipputuotoille ei ole asiaa, ellei volatiliteetti ole hallinnassa eli riittävän alhainen (alle mediaanin).
11/
 Voimme myös katsoa CAGR-kapasiteettia volatiliteetin funktiona.

Värit edustavat nyt mean excess returnin neljänneksiä.

Kuva kertoo, että tuotto-odotuksen on oltava parhaassa neljänneksessä, jotta supertuotot ovat mahdollisia. Edelleen suuri vola tappaa CAGR-kapasiteetin.
12/
 Päivän päätteeksi parametrien kuningas on kuitenkin Sharpe ratio.

Sharpe ratio yksinään määrittää geometrisen risk premiumin kapasiteetin (riskittömän koron päälle kertyvän maksimituoton) ja yhdessä riskittömän koron kanssa CAGR-kapasiteetin.
13/
 Miltä maksimi-CAGR ja Full Kellyn drawdownit ovat näyttäneet historiassa?

CAGR on suuri, mutta ei yllä teoreettiseen arvoonsa, koska vipu rebalansoidaan liian harvoin (kuukausittain). 25 periodilla menetetään koko oma pääoma. Drawdownit järkyttänevät jopa selvännäkijää.
14/
 Puolittamalla maksimivipu päästään jo siedettävämmän näköisiin lukemiin.

Drawdownit ovat edelleen suuria, mutta odotetusti keskimäärin noin puolet maksimivivun vastaavista.

Kuukausittainen rabalansointi on riittävä ja realisoitunut CAGR on samaa luokkaa Full Kellyn kanssa.
15/
 0.265 Kellyllä päästään keskimäärin 100% osakeallokaatioon. Voimme siis verrata dynaamista selvännäkijän allokaatiota staattiseen 100% allokaatioon.

GAGR on suurempi ja erityisesti maksimi drawdownit ovat pienempiä. Mean(CAGR)/mean(maxDD) on noin 2.5-kertainen.
16/
 10 vuoden periodiin ja kahteen parametriin rajoitettu selvännäkijä siis odotetusti hakkaa staattisen allokaation sekä CAGRlla mitattuna, että riskikorjattuna.

Me kuolevaiset emme näe tulevaisuutta, jolloin olemme pakotettuja ennusteisiin ja peli vaikeutuu kertaheitolla.
17/
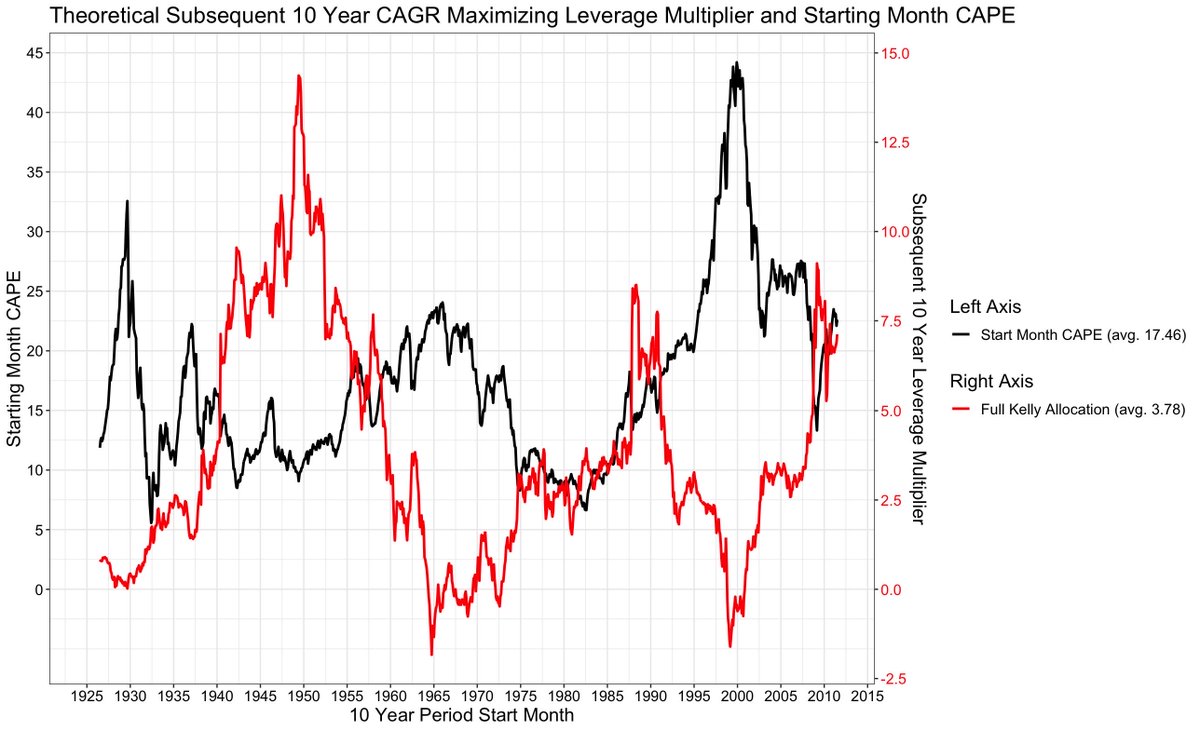
 CAPE tunnetusti ennustaa pitkän aikavälin tuottoja, joten kokeillaan sitä.

Katsotaan ensin silmällä. CAPElla ja optimaalisella seuraavan 10 vuoden sijoitusasteella näyttäisi olevan negatiivinen korrelaatio.
18/
 Mutta se sama viuhkamainen muoto on näkyvillä myös CAPEn ennustamassa sijoitusasteessa.

Suurella CAPElla on selkeästi vaadittu pieni allokaatio, mutta pienellä CAPElla volatiliteetti nousee taas ratkaisevaksi tekijäksi ja CAPE yksin ei anna selkeää vastausta.
19/
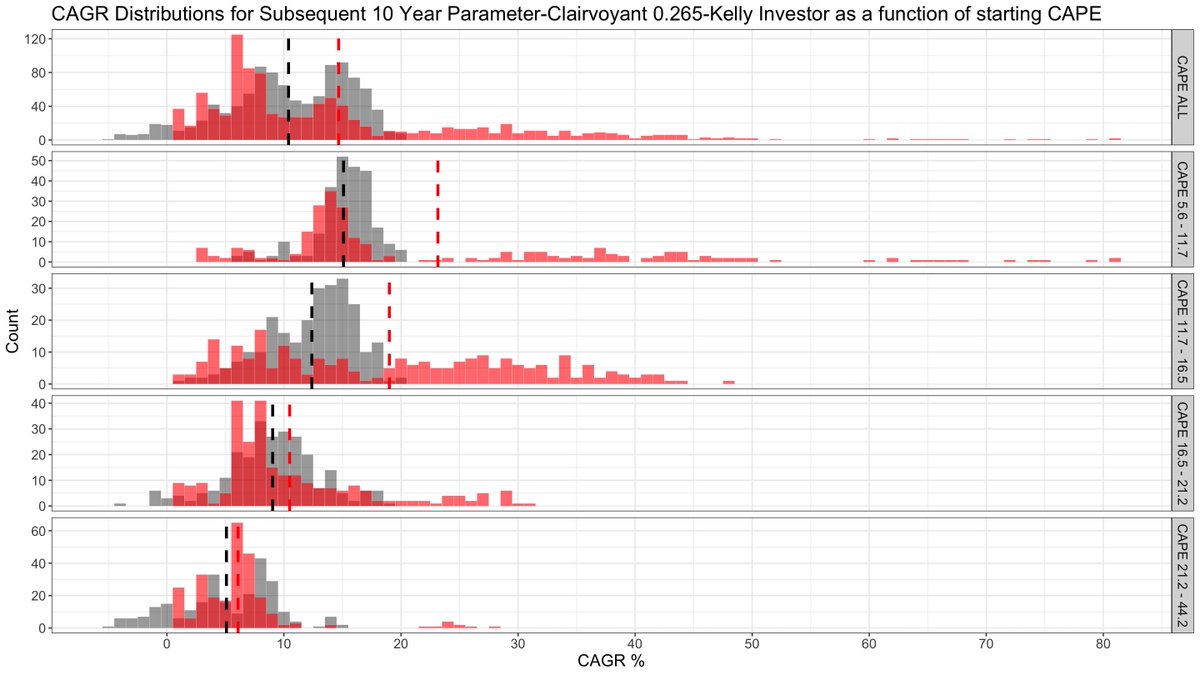
 Tarkastellaan sijoitusasteen jakaumia CAPE-neljänneksittäin 0.265-Kelly allokaatiolla (keskimäärin 100% allokaatio).

Allokaatio on keskiarvona 1.4 kun CAPE on alle mediaaninsa ja laskee alle 0.5 kun CAPE on kalleimmillaan. Halvalla CAPElla on ikävän paljon hajontaa.
20/
 CAGR (punainen dynaaminen 0.265-Kelly, musta/harmaa staattinen strategia) etu syntyy CAPEn ollessa alle mediaaninsa.

Etu kuitenkin näyttää syntyvän pitkälti harvinaisemmista supertuotoista, jotka ovat CAPE-neljänneksen sisällä onnistuneesti ajoitetun vivun tuottamia.
21/
 Dynaaminen selvännäkijä välttää kalliille CAPElle tyypilliset suuret drawdownit tehokkaasti.

Pieni allokaatio kalliin CAPEn aikana auttaa. Selvännäkijä pystyykin pitämään drawdown-riskinsä hyvin vakiona CAPEsta riippumatta.
22/
 Yhteenvetona:

Sharpe määrittää riskikorjatun tuoton, mutta myös CAGR kapasiteetin.

Volalla on suuri rooli optimaalisen sijoitusasteen kannalta.

CAPE ennustaa optimaalista sijoitusastetta, mutta sen ennustusvoima yksinään vaikuttaa heikolta halvassa markkinassa.

/END

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with Markku Kurtti

Markku Kurtti Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @markku_kurtti

Markku Kurtti Profile picture
Aug 22
1/9
I just finished an excellent book ’Advanced Portfolio Management: A Quant's Guide for Fundamental Investors’ by @__paleologo

The book is intended mainly for fundamental managers to help them express their ideas as portfolios. Image
2/9
I’m not a fundamental manager and have no alpha, but being a quant enthusiastic, this book provided a lot of food for thought and ignited some thought processes which now keep seeking their way up to the active tasks list.
3/9
Importantly, the book is written by an actual practitioner. We get a glimpse of the portfolio and risk management methods used in some of the most succesful hedge funds instead of just the academic theory.
Read 9 tweets
Markku Kurtti Profile picture
Jan 21, 2023
1/
🧵How much skill (alpha) a concentrated stock picker needs to beat a fully diversified benchmark index?

Variance lowers expected geometric return. To compensate for the idiosyncratic variance drag, stock picker needs skill to catch up with and to exceed the index return.
2/
We:
- Consider geometric (instead of arithmetic) returns
- Assume continuously compounded returns, equally weighted portfolios & similar volatility for portfolios of equal size
- Completely ignore the risk reduction aspect of diversification and focus only on expected returns
3/
This aspect of increasing expected return as a function of diversification is almost completely ignored by conventional finance theory, which utilizes arithmetic returns to assess diversification.

At the same time, ~100% of long-term investors care about geometric return.
Read 12 tweets
Markku Kurtti Profile picture
Jan 5, 2023
1/23

🧵 The importance of diversification increases with time

In the absence of stock picking skill, compound wealth of a typical poorly diversified portfolio loses to compound wealth of a fully diversified benchmark the more the longer the time horizon.
2/
Probably the best known phrase in finance is ”diversification is a free lunch” by Markowitz.

This is true for annualized arithmetic (single period, no compounding) returns, for which mean remains constant while spread of returns narrows with diversification. Image
3/
In real life, however, returns compound over time and we therefore care about geometric returns at portfolio level.

Now diversification is no longer free, but a negative price lunch. Average annualized geometric return increases with diversification. Image
Read 36 tweets
Markku Kurtti Profile picture
Nov 26, 2022
1/15

🧵 Consider a parameter-clairvoyant Kelly investor

The clairvoyant can borrow at risk-free rate, is immune to margin calls and can foresee two parameters for the next ten years: Sharpe ratio and volatility.

Having this gift, he can optimize leverage to maximize his CAGR.
2/
CAGR is maximized at full Kelly allocation, i.e. when portfolio’s volatility (fs) = Sharpe ratio (SR). f = leverage multiplier, s = volatility at 100% allocation.

[Note that Kelly use continuously compounded growth rate g = ln(1 + CAGR). Both g and CAGR max at full Kelly]
3/
Let’s use U.S. (French) monthly data between Jul/1926 – Jun/2021 and plot the Kelly leverage multiplier and its constituents for the subsequent 10 year period.

Leverage multiplier varies wildly between min -1.83 (Oct/1964) and max 14.36 (Jun/1949). Image
Read 15 tweets
Markku Kurtti Profile picture
Aug 16, 2022
1/6
🧵 The Shannon limit

Digital communications:

Information channel capacity =
The max achievable average error-free data transfer rate over a noisy channel

Finance:

Compounding process capacity =
The max achievable average compound excess growth rate for a risky investment Image
2/6
Given a sufficient frequency bandwidth, information channel capacity depends only on signal-to-noise(per Hz) ratio (SNR).

Given a sufficient compounding frequency, compounding process capacity depends only on square of Sharpe ratio, the SNR of arithmetic excess returns.
3/6
With continuous compounding and rebalancing, compounding process capacity (C) reduces to:

C = SR^2/2

setting a theoretical upper bound to portfolio’s long-term expected excess growth rate

We can see empirically how C sets the limit which is approached, but never exceeded:
Read 6 tweets
Markku Kurtti Profile picture
Aug 11, 2022
1/5
Your expected growth rate and optimal leverage are lower than you estimate

Why?

Because you not only need to account for volatility drag, but also the drag from volatility (uncertainty) of your volatility estimate.

Unlike realized past, future always entails uncertainty.
2/5
We can derive

Kelly criterion:
f* = (m-r)/(Mean(SDest)^2+SD(SDest)^2)

and

Geometric risk premium:
g-r = f(m-r) - f^2(Mean(SDest)^2+SD(SDest)^2)/2

in the presence of uncertainty about risk SD(SDest)

f = leverage multiplier
m = arith. mean
g = geom. mean
r = riskless rate
3/5
SD(SDest) = 0 for realized past, but always > 0 for the future

Implications?

Uncertainty about risk may be a function of investment time horizon.

There is a lot of noise at short horizons, but on the other hand the number of unknown unknowns realizing increase with time.
Read 5 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Don't want to be a Premium member but still want to support us?

Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal

Or Donate anonymously using crypto!

Ethereum

0xfe58350B80634f60Fa6Dc149a72b4DFbc17D341E copy

Bitcoin

3ATGMxNzCUFzxpMCHL5sWSt4DVtS8UqXpi copy

Thank you for your support!

Follow Us!

Send Email!

:(