
Engineer exploring the world of investing. Author of the investing blog https://t.co/vKZMEyYyM2
How to get URL link on X (Twitter) App


https://twitter.com/markku_kurtti/status/19096244077036299042/12


 2/9
2/9
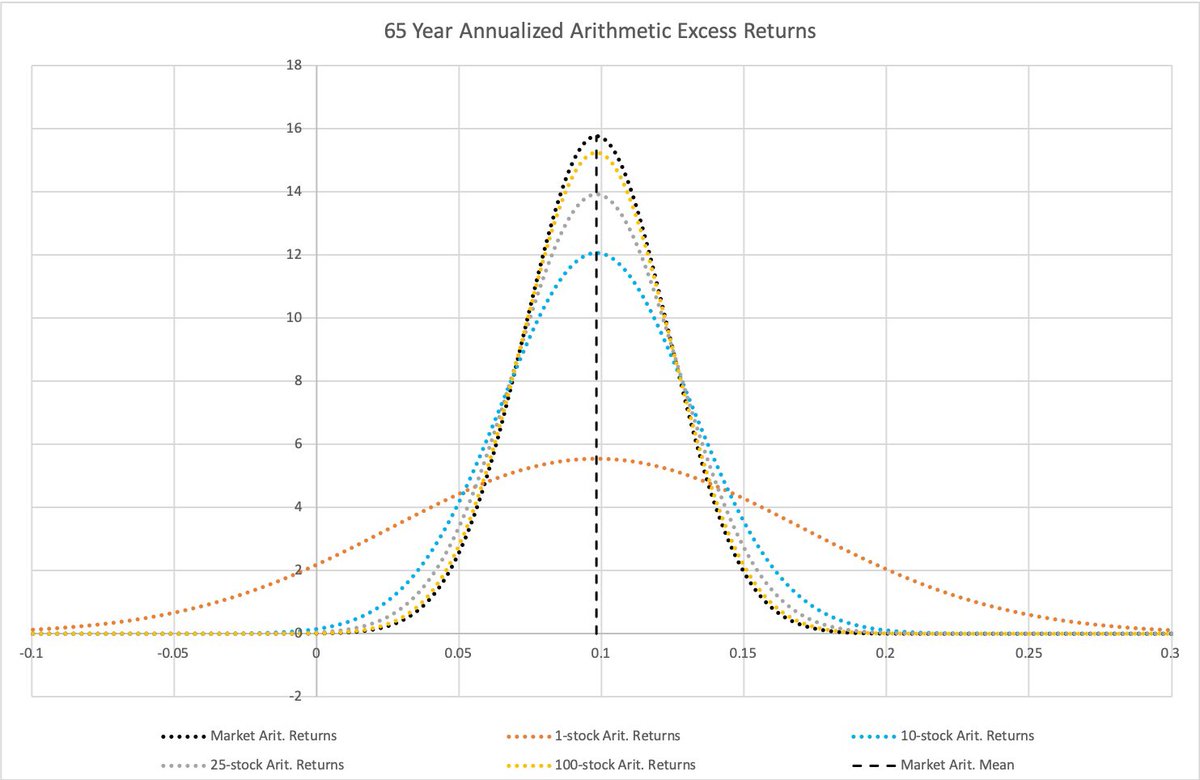


https://twitter.com/markku_kurtti/status/1541415451426693121

 2/6
2/6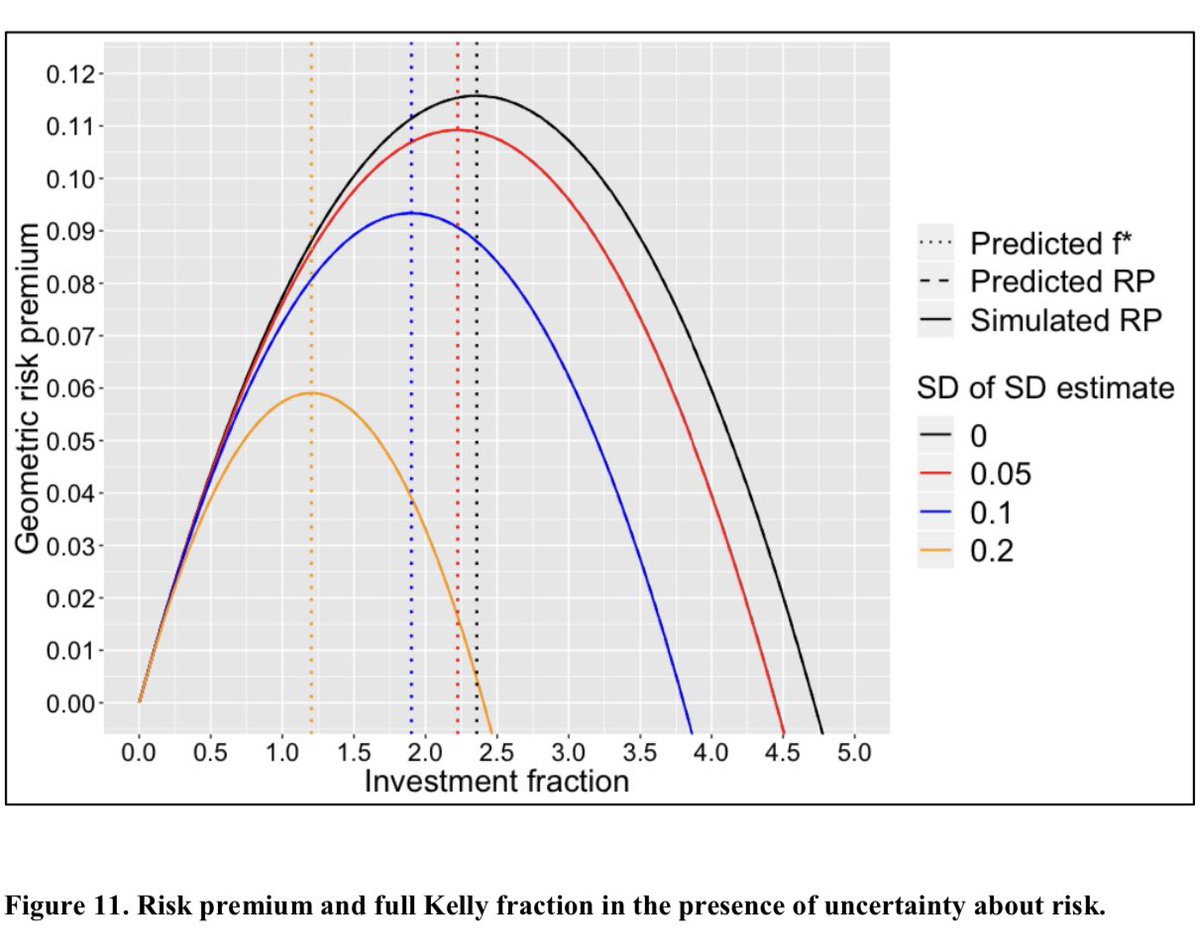
 2/5
2/5
 2/5
2/5





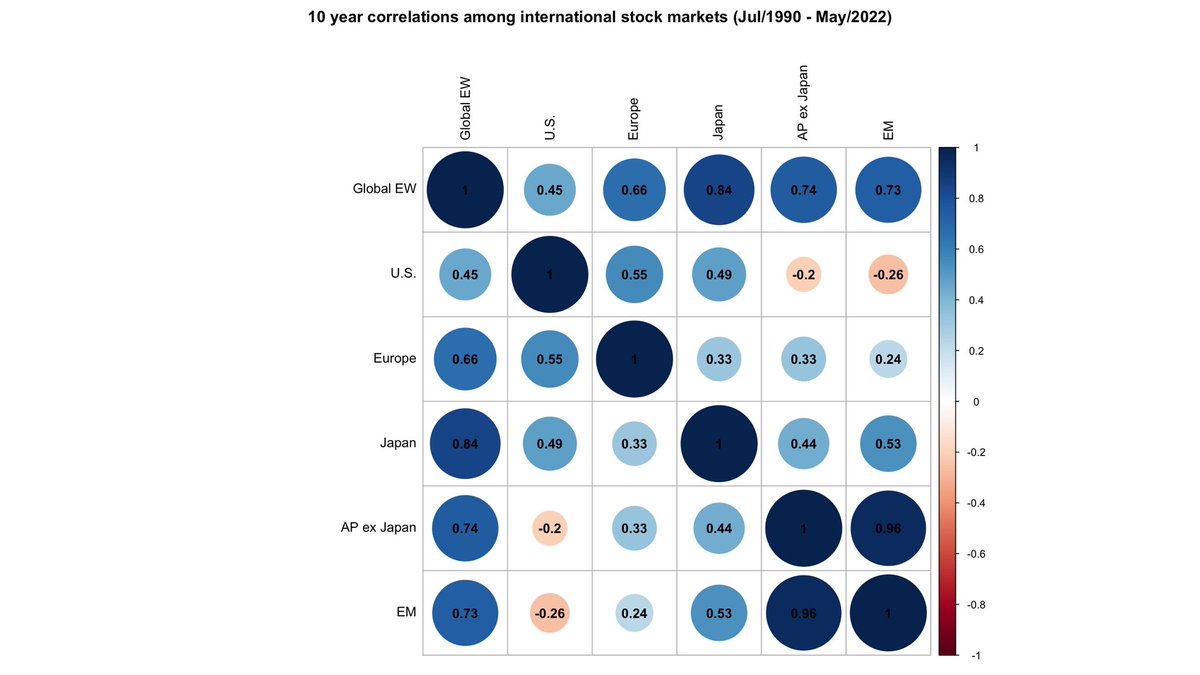 2/11
2/11
 2/7
2/7https://twitter.com/markku_kurtti/status/1541415451426693121

https://twitter.com/hkeskiva/status/1484806544063614977?s=21