26/55
E como essas estimativas são feitas? Como eu posso confiar nelas? Agora vou tentar destrinchar alguns detalhes de modelagem. Acredito que todos já estejam familiarizados com o conceito do numero de reprodução básico Rₜ (comenta nesse tweet se não estiver)
E como essas estimativas são feitas? Como eu posso confiar nelas? Agora vou tentar destrinchar alguns detalhes de modelagem. Acredito que todos já estejam familiarizados com o conceito do numero de reprodução básico Rₜ (comenta nesse tweet se não estiver)
27/55
Acima de 1, epidemia cresce. Abaixo de 1, epidemia decresce. Em 1, ela é estável. Acontece que esse numero muda com o tempo devido a todos os fatores mencionados nos tweets acima. O valor de R depende principalmente de 3 coisas:
Acima de 1, epidemia cresce. Abaixo de 1, epidemia decresce. Em 1, ela é estável. Acontece que esse numero muda com o tempo devido a todos os fatores mencionados nos tweets acima. O valor de R depende principalmente de 3 coisas:
28/55
1 - O valor de Rₜ no início da epidemia, sem alterações comportamentais na população ou medidas de intervenção, o chamado R0.2 - A medida de intervenção ativa no momento ou a mudança adotada pela população
1 - O valor de Rₜ no início da epidemia, sem alterações comportamentais na população ou medidas de intervenção, o chamado R0.2 - A medida de intervenção ativa no momento ou a mudança adotada pela população
29/55
3 - A aleatoriedade latente, ela trás as mudanças aleatórias que ocorrem em uma sociedade que alteram o Rₜ, como a população de um local aderir mais a uma medida de intervenção do que outro local
3 - A aleatoriedade latente, ela trás as mudanças aleatórias que ocorrem em uma sociedade que alteram o Rₜ, como a população de um local aderir mais a uma medida de intervenção do que outro local
30/55
Em termos matemáticos, isso é descrito da seguinte forma, os subíndices indicam que o valor de Rₜ é calculado em um instante específico “t” e uma localidade “l” para um conjunto “i” de intervenções.
Em termos matemáticos, isso é descrito da seguinte forma, os subíndices indicam que o valor de Rₜ é calculado em um instante específico “t” e uma localidade “l” para um conjunto “i” de intervenções.

31/55
Em tese, o R0 é escolhido para representar o período pré intervenções e mudanças comportamentais. Mas, já que estamos interessados em medir o efeito das intervenções COM as mudanças comportamentais já na sociedade
Em tese, o R0 é escolhido para representar o período pré intervenções e mudanças comportamentais. Mas, já que estamos interessados em medir o efeito das intervenções COM as mudanças comportamentais já na sociedade
32/55
É interessante escolher um R0 de um período sem intervenções, mas mais para frente da pandemia. Assim a base de comparação do efeito das intervenções é já um período onde a população havia incorporado mudanças sociais devido à pandemia
É interessante escolher um R0 de um período sem intervenções, mas mais para frente da pandemia. Assim a base de comparação do efeito das intervenções é já um período onde a população havia incorporado mudanças sociais devido à pandemia
33/55
Nesse artigo, os autores escolheram como estimativa de R0, o período de Agosto de 2020, quando muitos países europeus liberaram as restrições e o fator que mais continha o crescimento de R0 era principalmente o próprio comportamento social da população.
Nesse artigo, os autores escolheram como estimativa de R0, o período de Agosto de 2020, quando muitos países europeus liberaram as restrições e o fator que mais continha o crescimento de R0 era principalmente o próprio comportamento social da população.

34/55
O efeito de uma intervenção é dado pelo parâmetro de efeito β. Os autores assumem que β depende apenas do tipo de intervenção e não muda entre locais ou o tempo.
O efeito de uma intervenção é dado pelo parâmetro de efeito β. Os autores assumem que β depende apenas do tipo de intervenção e não muda entre locais ou o tempo.

35/55
Isso poderia ser uma limitação forte no modelo, mas a latência aleatória é responsável por trazer mudanças aleatórias na redução de Rₜ, que podem ocorrer entre locais e entre instantes de tempo diferentes.
Isso poderia ser uma limitação forte no modelo, mas a latência aleatória é responsável por trazer mudanças aleatórias na redução de Rₜ, que podem ocorrer entre locais e entre instantes de tempo diferentes.

36/55
A latência aleatória é dada por um random walk, ou caminhar aleatório que pode acabar representando dinâmicas diferentes para a intervenção. Ela pode ter seu efeito diluído com o tempo, ou aumentado, ou um local pode ter um efeito maior e mais duradouro.
A latência aleatória é dada por um random walk, ou caminhar aleatório que pode acabar representando dinâmicas diferentes para a intervenção. Ela pode ter seu efeito diluído com o tempo, ou aumentado, ou um local pode ter um efeito maior e mais duradouro.
37/55
O random walk trás essa variação. Random walk é um ruído aleatório que é adicionado ao valor de Rₜ para representar possíveis caminhos que o Rₜ pode seguir
Agora que vimos como Rₜ muda, resta saber como ele se conecta com os casos e como extraímos ele dos nossos dados.
O random walk trás essa variação. Random walk é um ruído aleatório que é adicionado ao valor de Rₜ para representar possíveis caminhos que o Rₜ pode seguir
Agora que vimos como Rₜ muda, resta saber como ele se conecta com os casos e como extraímos ele dos nossos dados.
38/55
O Rₜ nos diz a proporção de casos secundários que um infectado causa. Portanto, a princípio, seria apenas aplicar a razão (Casos hoje/Casos ontem), e teríamos o valor de Rₜ.
O Rₜ nos diz a proporção de casos secundários que um infectado causa. Portanto, a princípio, seria apenas aplicar a razão (Casos hoje/Casos ontem), e teríamos o valor de Rₜ.
39/55
Mas as coisas não são simples assim. Nem sempre um infectado infecta alguém já no dia seguinte. Isso leva um tempo. Esse tempo que leva entre infecções é chamado de intervalo entre gerações.
Mas as coisas não são simples assim. Nem sempre um infectado infecta alguém já no dia seguinte. Isso leva um tempo. Esse tempo que leva entre infecções é chamado de intervalo entre gerações.
40/55
Ele é dado em termos de uma distribuição de probabilidade que nos diz a proporção de infecções secundárias que ocorreram entre x e x+1 dias após a infecção. Essa é a forma da distribuição de intervalo de geração da COVID-19.
Ele é dado em termos de uma distribuição de probabilidade que nos diz a proporção de infecções secundárias que ocorreram entre x e x+1 dias após a infecção. Essa é a forma da distribuição de intervalo de geração da COVID-19.

41/55
Nela, a área da curva entre dois dias nos dá a probabilidade de que um caso secundário seja gerado entre os dois dias. Nessa distribuição abaixo, a probabilidade de um caso secundário ocorrer entre o dia 3 e 4 após a infecção é de 21.7%. Caso tenham duvidas, comentem aqui
Nela, a área da curva entre dois dias nos dá a probabilidade de que um caso secundário seja gerado entre os dois dias. Nessa distribuição abaixo, a probabilidade de um caso secundário ocorrer entre o dia 3 e 4 após a infecção é de 21.7%. Caso tenham duvidas, comentem aqui

42/55
Levando em conta então o intervalo entre gerações, o numero de casos hoje Nₜ é dado pelo numero de reprodução Rₜ vezes a quantidade de casos nos últimos dias, multiplicados pelo intervalo de gerações em cada dia, para sabermos quantos dos casos passados geraram casos hoje
Levando em conta então o intervalo entre gerações, o numero de casos hoje Nₜ é dado pelo numero de reprodução Rₜ vezes a quantidade de casos nos últimos dias, multiplicados pelo intervalo de gerações em cada dia, para sabermos quantos dos casos passados geraram casos hoje

43/55
Além disso, há outra coisa que precisa ser considerada. Uma vez infectado, uma pessoa ainda precisa ser testada e ter o resultado. Isso leva tempo. Por isso, o numero de casos hoje N só vai ser reportado após uma quantia de tempo Pc.
Além disso, há outra coisa que precisa ser considerada. Uma vez infectado, uma pessoa ainda precisa ser testada e ter o resultado. Isso leva tempo. Por isso, o numero de casos hoje N só vai ser reportado após uma quantia de tempo Pc.

44/55
Novamente, Pc é dado por uma distribuição que nos diz a probabilidade de um caso ser reportado x dias após a infecção.
Novamente, Pc é dado por uma distribuição que nos diz a probabilidade de um caso ser reportado x dias após a infecção.
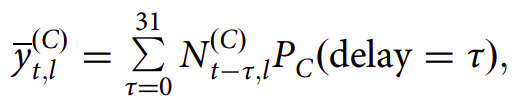
45/55
Ok, temos muitas coisas aqui. Mas notem que quase tudo já é conhecido. Sabemos a forma da distribuição do intervalo de geração, do intervalo entre infecção e notificação, temos acesso à quantidade de casos no passado
Ok, temos muitas coisas aqui. Mas notem que quase tudo já é conhecido. Sabemos a forma da distribuição do intervalo de geração, do intervalo entre infecção e notificação, temos acesso à quantidade de casos no passado
46/55
Sabemos a quantidade de casos hoje e o valor de R0 antes das intervenções. Assim, o único real parâmetro desconhecido é o β.
Sabemos a quantidade de casos hoje e o valor de R0 antes das intervenções. Assim, o único real parâmetro desconhecido é o β.
47/55
Levando tudo isso em consideração, calcula-se o valor de Rₜ para os períodos durante uma ou mais intervenções aplicadas e estima-se o valor de β para cada uma delas. Dessa forma, podemos saber o quão eficaz uma medida de intervenção foi (o quanto diminuiu a transmissão).
Levando tudo isso em consideração, calcula-se o valor de Rₜ para os períodos durante uma ou mais intervenções aplicadas e estima-se o valor de β para cada uma delas. Dessa forma, podemos saber o quão eficaz uma medida de intervenção foi (o quanto diminuiu a transmissão).
48/55
Uma coisa interessante é que β não necessariamente é obrigado a ser positivo (a demonstrar efeito para a medida de intervenção). Ele pode ser 0 e até mesmo negativo, caso a medida seja realmente muito ruim.
Uma coisa interessante é que β não necessariamente é obrigado a ser positivo (a demonstrar efeito para a medida de intervenção). Ele pode ser 0 e até mesmo negativo, caso a medida seja realmente muito ruim.

49/55
Isso é muito importante, pois restringindo β para valores positivos nós forçamos o modelo a encontrar alguma efetividade, o que é enviesar o resultado, por isso neste artigo β não é forçado para valores positivos. Isso é o efeito da escolha de priori no modelo
Isso é muito importante, pois restringindo β para valores positivos nós forçamos o modelo a encontrar alguma efetividade, o que é enviesar o resultado, por isso neste artigo β não é forçado para valores positivos. Isso é o efeito da escolha de priori no modelo
50/55
Essa é honestamente a parte que eu mais gosto em artigos que envolvem modelagem matemática, entender o modelo e comparar com a realidade. Claro que ainda há fatores que podem ser inclusos, como a heterogeneidade por idade.
Essa é honestamente a parte que eu mais gosto em artigos que envolvem modelagem matemática, entender o modelo e comparar com a realidade. Claro que ainda há fatores que podem ser inclusos, como a heterogeneidade por idade.
51/55
Como cada faixa etária tem padrões de contato diferentes, seria mais justo estimar um Rₜ para cada faixa etária, afim de compor o Rₜ total a partir destes Rs.
Como cada faixa etária tem padrões de contato diferentes, seria mais justo estimar um Rₜ para cada faixa etária, afim de compor o Rₜ total a partir destes Rs.
52/55
Ou então incluir um outro termo que muda Rₜ que esteja associado à presença de variantes. Por exemplo, pode-se dizer que do período de X até Y, R0 vale 1.7, já de Y para frente, R0 vale 2.1 devido à uma nova variante com transmissibilidade intrínseca maior.
Ou então incluir um outro termo que muda Rₜ que esteja associado à presença de variantes. Por exemplo, pode-se dizer que do período de X até Y, R0 vale 1.7, já de Y para frente, R0 vale 2.1 devido à uma nova variante com transmissibilidade intrínseca maior.
53/55
Entretanto, isso requer dados mais precisos, sabendo a quantidade de casos em cada faixa etária e sabendo a forma das distribuições mencionadas, bem como o R0 para cada faixa etária e específicos de cada variante. Aqui vemos uma barreira para fazer modelos + realísticos
Entretanto, isso requer dados mais precisos, sabendo a quantidade de casos em cada faixa etária e sabendo a forma das distribuições mencionadas, bem como o R0 para cada faixa etária e específicos de cada variante. Aqui vemos uma barreira para fazer modelos + realísticos
54/55
Frequentemente não temos dados que sirvam para eles. Modelagem matemática de fenômenos é um balanço entre modelos acurados com a realidade e a disponibilidade de dados para ajustá-los. Encontrar esse balanço com os dados disponíveis é incrível.
Frequentemente não temos dados que sirvam para eles. Modelagem matemática de fenômenos é um balanço entre modelos acurados com a realidade e a disponibilidade de dados para ajustá-los. Encontrar esse balanço com os dados disponíveis é incrível.
55/55
A capacidade de uso desses modelos é o que nos permite quantificar e estimar as incertezas em torno de medidas no mundo real.
Perdão pelo fio longo 😅 (Se você chegou até aqui tome esse gif)
A capacidade de uso desses modelos é o que nos permite quantificar e estimar as incertezas em torno de medidas no mundo real.
Perdão pelo fio longo 😅 (Se você chegou até aqui tome esse gif)
Divulgadores: @rizbicki @rafalpx @LaroccaRA @oatila @mellziland @LeSarturiP @leticiakawano @otavio_ranzani @leosbastos @mab_sp125 @TaschnerNatalia @luizacaires3 @leandrotessler @dogarrett @ntsnaleatorias @Capyvara @josegallucci @anarina @schrarstzhaupt @marciacastrorj @marfcg
Percebi que os pedaços do fio não estão juntos (maldito twitter), o começo é aqui
https://twitter.com/pedrocintra52/status/1494065468042268674
• • •
Missing some Tweet in this thread? You can try to
force a refresh













