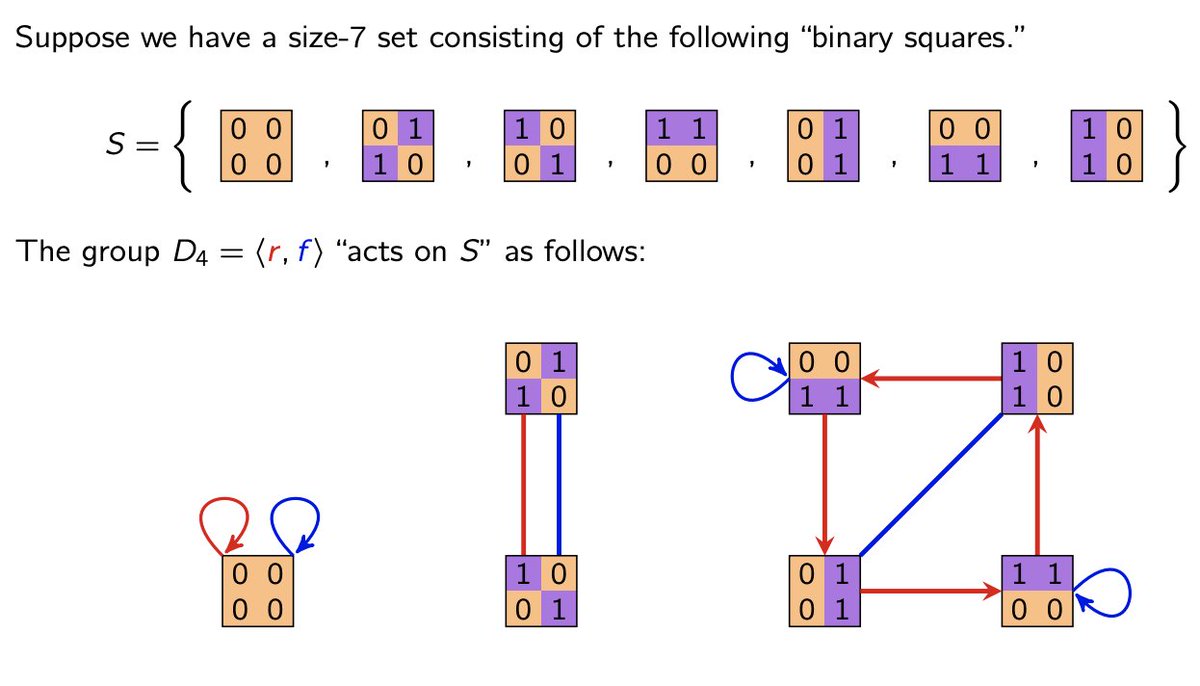
We started #Week7 in #VisualAlgebra yesterday with the tower law.
Here are two ways to think about it. One involves cosets as "boxes" in a grid, and the other is in terms of the subgroup lattice: to find the index [H:K], just take the product of the edges b/w them.
1/8 Mon

Here are two ways to think about it. One involves cosets as "boxes" in a grid, and the other is in terms of the subgroup lattice: to find the index [H:K], just take the product of the edges b/w them.
1/8 Mon


Pause for a quick comment about cosets in additive groups. Don't forget to write a+H, rather than aH. Here's a nice way to see the equality of a left coset and a right coset.
2/8 M

2/8 M


Next, we proved that if [G:H]=2, then H is normal. Here's a "picture proof": one left (resp., right) coset is H, and the other is G-H.
3/8 M
3/8 M

Next up: normalizers. In my experience, this is a concept that is easily forgotten, or not particularly memorable. I want to change that.
I will continue the convention of drawing xH:
BLUE <=> xH=Hx
RED <=> xH≠Hx.
The normalizer is just the union of blue cosets.
4/8 M
I will continue the convention of drawing xH:
BLUE <=> xH=Hx
RED <=> xH≠Hx.
The normalizer is just the union of blue cosets.
4/8 M

Here's an example, adapted from @nathancarter5's "Visual Group Theory" book, by adding the red/blue coloring scheme.
There are *2* red paths H-->rH: r & r^5. Color it RED.
There's a UNIQUE red path H-->r^3H. Color it BLUE.
5/8 M
There are *2* red paths H-->rH: r & r^5. Color it RED.
There's a UNIQUE red path H-->r^3H. Color it BLUE.
5/8 M

Next up: my favorite example, A_4.
REMEMBER THESE 3 SUBGROUPS! (we'll revisit them)
Notice how there are "fans" of:
--1 subgroup of order four (N)
--4 subgroups of order three (H,...)
--3 subgroups of order two (K,...)
Pay attention to these numbers!
6/8 M
REMEMBER THESE 3 SUBGROUPS! (we'll revisit them)
Notice how there are "fans" of:
--1 subgroup of order four (N)
--4 subgroups of order three (H,...)
--3 subgroups of order two (K,...)
Pay attention to these numbers!
6/8 M

Remember those numbers: 1, 4, and 3?
Where do you see those in this picture?
Their reciprocals are the "proportion of cosets that are blue".
In some sense, this measures "how close" to being normal a subgroup is. Let's formalize this! (next slide)
7/8 M
Where do you see those in this picture?
Their reciprocals are the "proportion of cosets that are blue".
In some sense, this measures "how close" to being normal a subgroup is. Let's formalize this! (next slide)
7/8 M

The "degree of normality" is not a standard definition, nor is it necessary. But it will make certain abstract statements cleaner later in the course, especially in Sylow theory.
Stay tuned for conjugacy Wed. We'll see a special case of the orbit-stabilizer thm w/ this.
8/8 M
Stay tuned for conjugacy Wed. We'll see a special case of the orbit-stabilizer thm w/ this.
8/8 M

Today was especially fun! The theme was how much we can we determine about a group and its subgroups simply by inspection of its subgroup lattice. The missing ingredient is conjugacy classes.
Let's revisit our 3 favorite subgroups of A_4.
1/14 Wed 🧵👆👇
Let's revisit our 3 favorite subgroups of A_4.
1/14 Wed 🧵👆👇

Note how conjugacy classes "fan out". The wider a fan, the "less normal" the subgroup.
These subgroups have 1, 4, and 3 conjugates, respectively. Where have we seen those numbers before? (Scroll up to Monday!)
This is the index of the normalizer!
2/14 W
These subgroups have 1, 4, and 3 conjugates, respectively. Where have we seen those numbers before? (Scroll up to Monday!)
This is the index of the normalizer!
2/14 W

Note that the following 2 things measure how close to being normal a subgroup is:
--index of normalizer (proport. of "blue cosets")^{-1}
--number of conj. subgroups (width of "fan")
But...these are exactly the same thing! 🤯
3/14 W
--index of normalizer (proport. of "blue cosets")^{-1}
--number of conj. subgroups (width of "fan")
But...these are exactly the same thing! 🤯
3/14 W

Sometimes, it's convenient to collapse conjugacy classes ("fans") into single nodes. The GroupNames website does this. We'll call this the "reduced lattice".
In some cases, this reveals patterns that are otherwise hidden!
(Note: left-subscript = size of conj. class).
4/14 W
In some cases, this reveals patterns that are otherwise hidden!
(Note: left-subscript = size of conj. class).
4/14 W

Now, let's consider conjugating a group by a fixed x∈G.
Subgroups at a "unique lattice neighborhood" are called UNICORNS. (Very useful def'n!)
We will always color unicorns purple (because duh).
We're intentionally leaving this definition vague.
5/14 W

Subgroups at a "unique lattice neighborhood" are called UNICORNS. (Very useful def'n!)
We will always color unicorns purple (because duh).
We're intentionally leaving this definition vague.
5/14 W


Here, <r^2> is a unicorn b/c it's the only order-2 subgroup with "3 parents". We see you x<r^2>x^{-1} -- you can't hide! Thus, x<r^2>x^{-1}=<r^2> for any x.
In other words: UNICORNS ARE NORMAL.
So are index-2 subgroups. Size-1 conjugacy classes are circled.
6/14 W

In other words: UNICORNS ARE NORMAL.
So are index-2 subgroups. Size-1 conjugacy classes are circled.
6/14 W

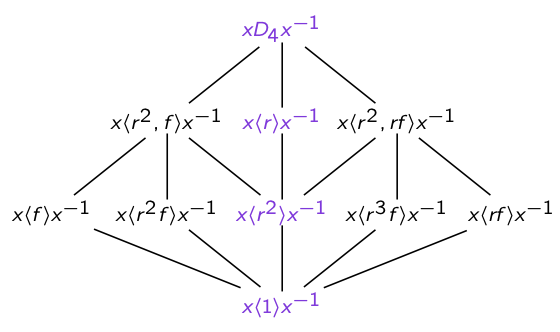
Now, what about the subgroup <f> of D_4?
Lemma: If |H|=2, then H⊲G iff H≤Z(G).
Since f isn't central, cl(<f>) has size at least 2. But it's contained in <r^2,f>. Thus, it MUST be
cl(<f>) = {<f>, <r^2f>}.
Same argument shows cl(<rf>) = {<rf>, <r^3f>}.
7/14 W
Lemma: If |H|=2, then H⊲G iff H≤Z(G).
Since f isn't central, cl(<f>) has size at least 2. But it's contained in <r^2,f>. Thus, it MUST be
cl(<f>) = {<f>, <r^2f>}.
Same argument shows cl(<rf>) = {<rf>, <r^3f>}.
7/14 W
Note that since |cl(H)| is the index of the normalizer, we know that the normalizers of all (non-normal) index-2 subgroups are just the order-4 subgroups above them.
We just classified the conjugacy classes of subgroups, AND all normalizers purely by inspection!
8/14 W
We just classified the conjugacy classes of subgroups, AND all normalizers purely by inspection!
8/14 W

Let's take a closer look at an argument we used.
Lemma: If H≤N⊲G, then xHx^{-1}≤N. (1-line proof)
Here's that argument we made about conjugacy classes in D_4, zoomed in. Remember: unicorns are purple.
<f> must be conjugate to SOMETHING in N (not <r^2>).
9/14 W
Lemma: If H≤N⊲G, then xHx^{-1}≤N. (1-line proof)
Here's that argument we made about conjugacy classes in D_4, zoomed in. Remember: unicorns are purple.
<f> must be conjugate to SOMETHING in N (not <r^2>).
9/14 W

I've intentionally been vague about the def'n of "unicorn".
It's basically "inv't under lattice automorphisms". But do we include isomorphism type?
Remember the diquaternion group? It has 4 cyclic subgroups of order 4. (Can you find them?)
10/14 W
It's basically "inv't under lattice automorphisms". But do we include isomorphism type?
Remember the diquaternion group? It has 4 cyclic subgroups of order 4. (Can you find them?)
10/14 W

Here's its subgroup lattice. All C_4 subgroups have 3 parents. But one is "not like the others".
Indeed, the leftmost one is contained in 3 *abelian* subgroups.
Every conjugate of it must as well. Thus it's normal!
Does that count as a unicorn? I'd say so.
11/14 W
Indeed, the leftmost one is contained in 3 *abelian* subgroups.
Every conjugate of it must as well. Thus it's normal!
Does that count as a unicorn? I'd say so.
11/14 W

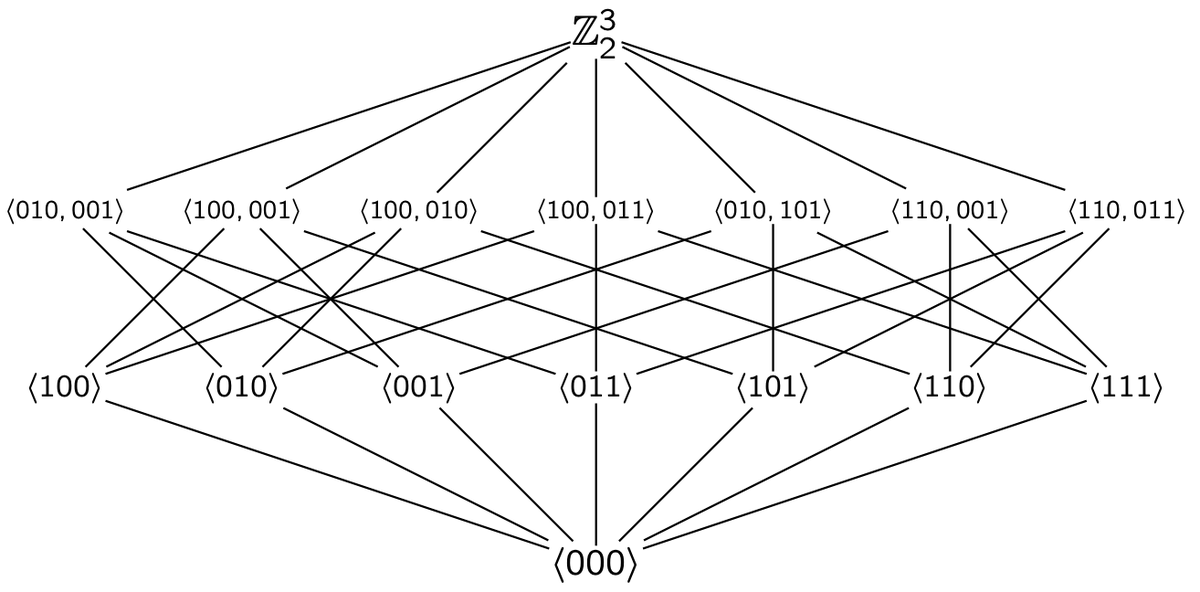
One more thing. On an earlier HW, we saw that the quotient of DQ_8 by the subgroup <-I> was isomorphic to Z_2^3. Its subgroup lattice is shown at right.
Go back unto the last tweet. Do you see that lattice stealthily hiding in the DQ_8 lattice?
HMMMMMMMM....... 🤯
12/14 W

Go back unto the last tweet. Do you see that lattice stealthily hiding in the DQ_8 lattice?
HMMMMMMMM....... 🤯
12/14 W

Here's a fun game: a MYSTERY GROUP of order 16.
Purple unicorns and index-2 subgroups are normal.
So basically everything except (possibly) <s> and <r^4s>.
IF they're normal, then s∈Z(G) => G is abelian.
Otherwise, cl(<s>)={<s>,<r^4s>}.
Which is it???
13/14 W

Purple unicorns and index-2 subgroups are normal.
So basically everything except (possibly) <s> and <r^4s>.
IF they're normal, then s∈Z(G) => G is abelian.
Otherwise, cl(<s>)={<s>,<r^4s>}.
Which is it???
13/14 W


Both are possible! Remember how C8xC2 and the semiabelian group SA_8 have the same cycle diagram, and both have a C4xC2 quotient? Well, they have the same subgroup lattice!
Unbelievable that 2.5 years ago, I wasn't even aware of this. I suspect that's not uncommon.
14/14 W

Unbelievable that 2.5 years ago, I wasn't even aware of this. I suspect that's not uncommon.
14/14 W


Wrapping up another week of #VisualAlgebra, we continued with conjugate subgroups.
They look like "fans" in the lattice. Key point: the "base" of a fan is always normal.
This gives strong restrictions on the structure of simple groups, such as A_5.
1/14 Fri 🧵👆👇

They look like "fans" in the lattice. Key point: the "base" of a fan is always normal.
This gives strong restrictions on the structure of simple groups, such as A_5.
1/14 Fri 🧵👆👇


Let's now turn to understanding conjugate subgroups algebraically.
Key point: if aH=bH, it is NOT necessarily true that Ha=Hb.
But it IS true that Ha^{-1}=Hb^{-1}. Here's a picture.
COROLLARY: if aH=bH, then aHa^{-1}=bHb^{-1}.
2/14 F
Key point: if aH=bH, it is NOT necessarily true that Ha=Hb.
But it IS true that Ha^{-1}=Hb^{-1}. Here's a picture.
COROLLARY: if aH=bH, then aHa^{-1}=bHb^{-1}.
2/14 F

Thus, to find all conjugate subgroups, take each left coset aH, and follow all a^{-1}-paths from those nodes on the Cayley diagram.
Let's try this with a few subgroups of C4⋊C4.
Exercise, show that we get the same result for the other left cosets (rows), and so A⊲G.
3/14 F
Let's try this with a few subgroups of C4⋊C4.
Exercise, show that we get the same result for the other left cosets (rows), and so A⊲G.
3/14 F

In contrast, here's that same process with a different subgroup of C4⋊C4.
This illustrates why B is not a normal subgroup.
Let's compute the other conjugates of B, by doing this process to the other 2 left cosets (columns 3 & 4)...
4/14 F
This illustrates why B is not a normal subgroup.
Let's compute the other conjugates of B, by doing this process to the other 2 left cosets (columns 3 & 4)...
4/14 F

On the left, we see that the coset a^2*B is in the normalizer of B!
On the right, we see that a^3*B is not.
So, the normalizer is N(B) = B ∪ a^2*B.
Note that B has 2 conjugates, and its normalizer has index 2.
5/14 F
On the right, we see that a^3*B is not.
So, the normalizer is N(B) = B ∪ a^2*B.
Note that B has 2 conjugates, and its normalizer has index 2.
5/14 F

Next up, products of groups. Given subgroups A,B, when is
AB := {ab | a∈A, b∈B}
a subgroup of G?
Ans: one must be in the normalizer of the other. Weaker but more useful condition: at least one is normal.
6/14 F


AB := {ab | a∈A, b∈B}
a subgroup of G?
Ans: one must be in the normalizer of the other. Weaker but more useful condition: at least one is normal.
6/14 F



Next up, formalizing quotients, a concept we've seen repetitively since the 2nd week of class, starting with Q_8. Here's the intuition we've had about what a quotient is.
Somehow, we're "collapsing" a group by a subgroup. But WHAT does this mean, and WHEN does it work?
7/14 F
Somehow, we're "collapsing" a group by a subgroup. But WHAT does this mean, and WHEN does it work?
7/14 F

Here's that same picture, but in terms of cosets -- a concept that we didn't have way back in Week 2.
REMINDER! I will continue to color-code a coset xH as
Blue: xH=Hx
Red: xH≠Hx.
8/14 F
REMINDER! I will continue to color-code a coset xH as
Blue: xH=Hx
Red: xH≠Hx.
8/14 F

Here's another example of a quotient, of an abelian group written additively. Once again, both cosets are blue -- this means the subgroup is normal.
9/14 F
9/14 F

Taking a quotient loses information. Here's a different group of order 6, that has a quotient to a group of size 2.
10/14 F
10/14 F

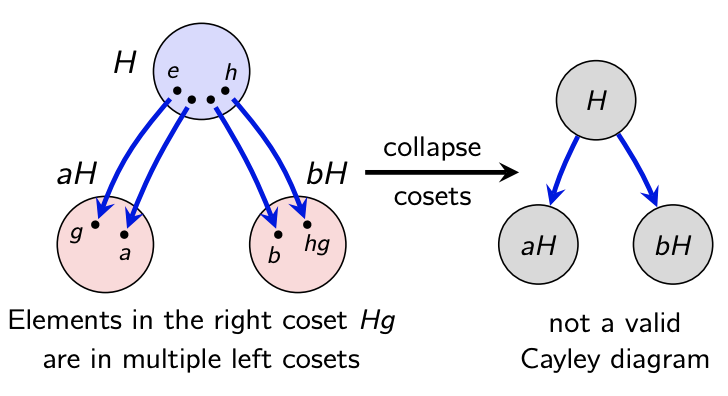
Here's an example of where the quotient process fails. Note that the subgroup is not normal. Collapsing it does NOT yield a valid Cayley diagram. There are 3 out-going blue arrows from each node.
11/14 F
11/14 F

So what is going on? This picture will serve as motivation for a formal algebraic proof.
The LEFT COSET gH is the "big node" containing g.
The RIGHT COSET Hg are the elts at the arrow tips.
These are NOT equal, and that's why the quotient fails.
12/14 F
The LEFT COSET gH is the "big node" containing g.
The RIGHT COSET Hg are the elts at the arrow tips.
These are NOT equal, and that's why the quotient fails.
12/14 F
In contrast, if H is normal, then the left and right cosets agree. All arrow tips end up in the same big node, and collapsing yields an unambiguous diagram.
This is what the definition WELL-DEFINED means.
A hard concept for many undergrads, in my experience.
13/14 F
This is what the definition WELL-DEFINED means.
A hard concept for many undergrads, in my experience.
13/14 F

Using our visuals as motivation, we formalized the quotient group algebraically:
aH*bH := abH
and proved that this definition is indeed well-defined.
Stay tuned for this week's HW, which I'll post tomorrow!
14/14 F
aH*bH := abH
and proved that this definition is indeed well-defined.
Stay tuned for this week's HW, which I'll post tomorrow!
14/14 F
• • •
Missing some Tweet in this thread? You can try to
force a refresh