There's been some back-and-forth about this paper on getting gradients without doing backpropagation, so I took a minute to write up an analysis on what breaks and how it might be fixed.
tl;dr: the estimated gradients are _really_ noisy! like wow
charlesfrye.github.io/pdfs/SNR-Forwa…
tl;dr: the estimated gradients are _really_ noisy! like wow
charlesfrye.github.io/pdfs/SNR-Forwa…
https://twitter.com/arankomatsuzaki/status/1494488254304989228
The main result I claim is an extension of Thm 1 in the paper. They prove that the _expected value_ of the gradient estimate is the true gradient, and I worked out the _variance_ of the estimate.
It's big! Each entry has variance equal to the entire true gradient's norm😬
It's big! Each entry has variance equal to the entire true gradient's norm😬
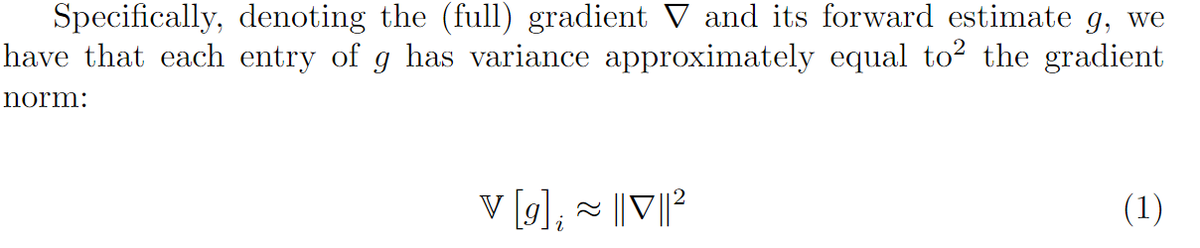
(Sketch of the proof: nothing is correlated, everything has 0 mean and is symmetric around the origin, the only relevant terms are chi-squared r.v.s with known variances that get scaled by the gradient norms. gaussians are fun!)
Informally, we say that "noisy gradients" are bad and slow down learning.
So I looked at the "signal to noise ratio" between the true gradient value and the variance of the estimate.
It's bad! If you're scaling your gradients properly, it gets worse as you add parameters.
So I looked at the "signal to noise ratio" between the true gradient value and the variance of the estimate.
It's bad! If you're scaling your gradients properly, it gets worse as you add parameters.

(FYI, I sanity-checked my result by pulling gradients from a PyTorch MNIST example and checking the true gradient's norm against the average variance of each entry, which should be equal. And they were super close!) 

I give some intuitions for the variance, and for the general distribution of the forward gradients (g), based on product distributions and large random vectors. 

In that paragraph I mention some simulations (related to the sanity check above). I didn't include the plots, but here they are! The alignment between the forward grad and the true gradient is all over the place -- and way worse than randomness from minibatch effects. 

More could've been said about the weaknesses of FG in the paper, but I don't think it's a useless idea.
So I wrote some suggestions. For example, if you already have a good prior about the gradient direction, maybe you could sample from it instead of a unit normal?
So I wrote some suggestions. For example, if you already have a good prior about the gradient direction, maybe you could sample from it instead of a unit normal?

@theshawwn i saw you expressing interest in the forward gradient stuff and reasonable skepticism about the value of MNIST experiments
this is a fairly rigorous argument that the gradient noise is too high for fwd grads, as is, to work in large models
this is a fairly rigorous argument that the gradient noise is too high for fwd grads, as is, to work in large models
For more details, especially on the derivation of the variance, see this short note I wrote up: charlesfrye.github.io/pdfs/SNR-Forwa…
• • •
Missing some Tweet in this thread? You can try to
force a refresh