🚨Job talk thread🚨
Title: What Can *Conformal Inference* Offer to Statistics?
Slides: lihualei71.github.io/Job_Talk_Lihua…
Main points:
(1) Conformal Inference can be made applicable in many #stats problems
(2) There are lots of misconceptions about Conformal Inference
(3) Try it!
1/n
Title: What Can *Conformal Inference* Offer to Statistics?
Slides: lihualei71.github.io/Job_Talk_Lihua…
Main points:
(1) Conformal Inference can be made applicable in many #stats problems
(2) There are lots of misconceptions about Conformal Inference
(3) Try it!
1/n

Conformal Inference was designed for generating prediction intervals with guaranteed coverage in standard #ML problems.
Nevertheless, it can be modified to be applicable in
✔️Causal inference
✔️Survival analysis
✔️Election night model
✔️Outlier detection
✔️Risk calibration
2/n
Nevertheless, it can be modified to be applicable in
✔️Causal inference
✔️Survival analysis
✔️Election night model
✔️Outlier detection
✔️Risk calibration
2/n

Misconceptions about conformal inference:
❌ Conformal intervals only have marginal coverage and tend to be wide
✔️ Conformal intervals w/ proper conformity scores achieve conditional coverage & efficiency (short length) if the model is correctly specified
3/n
❌ Conformal intervals only have marginal coverage and tend to be wide
✔️ Conformal intervals w/ proper conformity scores achieve conditional coverage & efficiency (short length) if the model is correctly specified
3/n

Misconceptions about conformal inference:
❌ Conformal inference is slow
✔️ Split conformal inference incurs almost negligible computational overhead (nearly as fast as the algorithm it wraps around)
4/n
❌ Conformal inference is slow
✔️ Split conformal inference incurs almost negligible computational overhead (nearly as fast as the algorithm it wraps around)
4/n
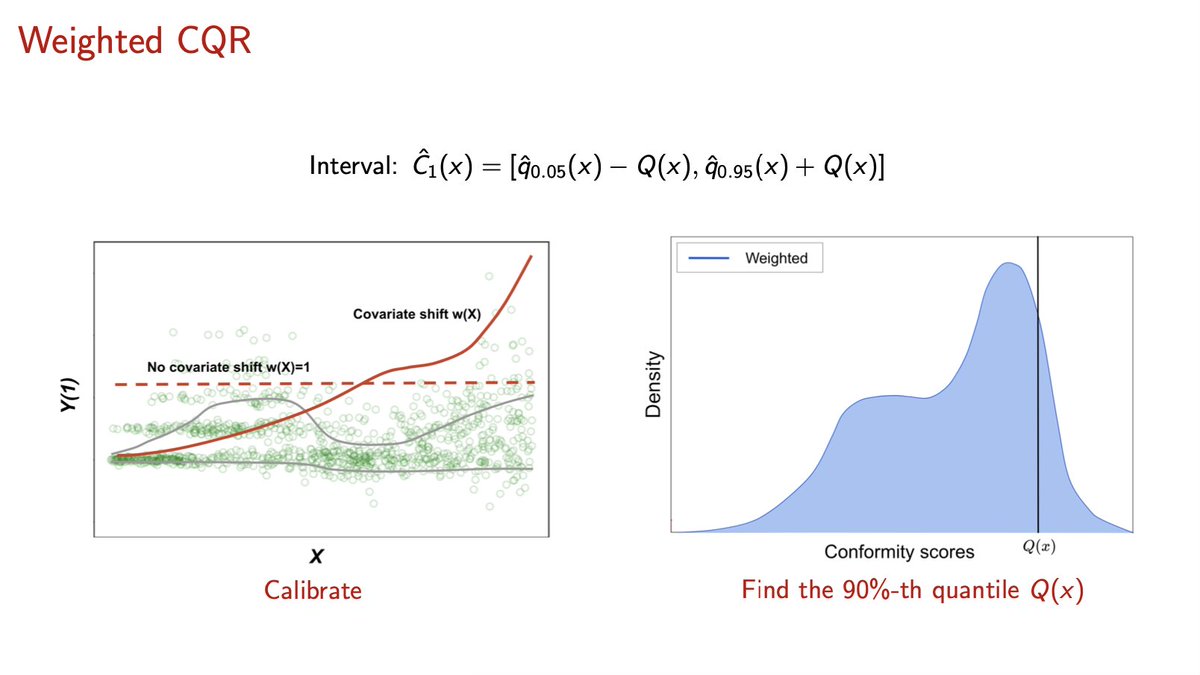
Misconceptions about conformal inference:
❌ Conformal inference can’t be used with Bayesian procedures
✔️ Conformal inference can not only wrap around Bayesian methods, but also achieve the validity (w/ a simple adjustment) in both Bayesian and Frequentist sense.
5/n
❌ Conformal inference can’t be used with Bayesian procedures
✔️ Conformal inference can not only wrap around Bayesian methods, but also achieve the validity (w/ a simple adjustment) in both Bayesian and Frequentist sense.
5/n

I’m so proud that my job talk convinced many folks to read more about Conformal Inference. There are tons of exciting methodological questions (distribution shifts, dependence, conditional coverage, …) and real-world applications.
It’s a very🔥area now! Come and join us!
6/6
It’s a very🔥area now! Come and join us!
6/6
• • •
Missing some Tweet in this thread? You can try to
force a refresh