Thread by @TivadarDanka

Taking a walk can change the course of science.

Roaming the streets of Königsberg, Euler was working on a simple puzzle: can he cross each of the city's bridges exactly once? The answer was no. And so, graph theory was born.

↓ This is its story. ↓

At the time of Euler, the central part of Königsberg (now Kaliningrad) was split into four parts by the Pregel (now Pregolya) river, with seven bridges between them, as illustrated below.

The question is, can you cross each one exactly once during a single walk?

To answer this question, we don't have to study the particular geography and layout of Königsberg, only the islands and the bridges connecting them.

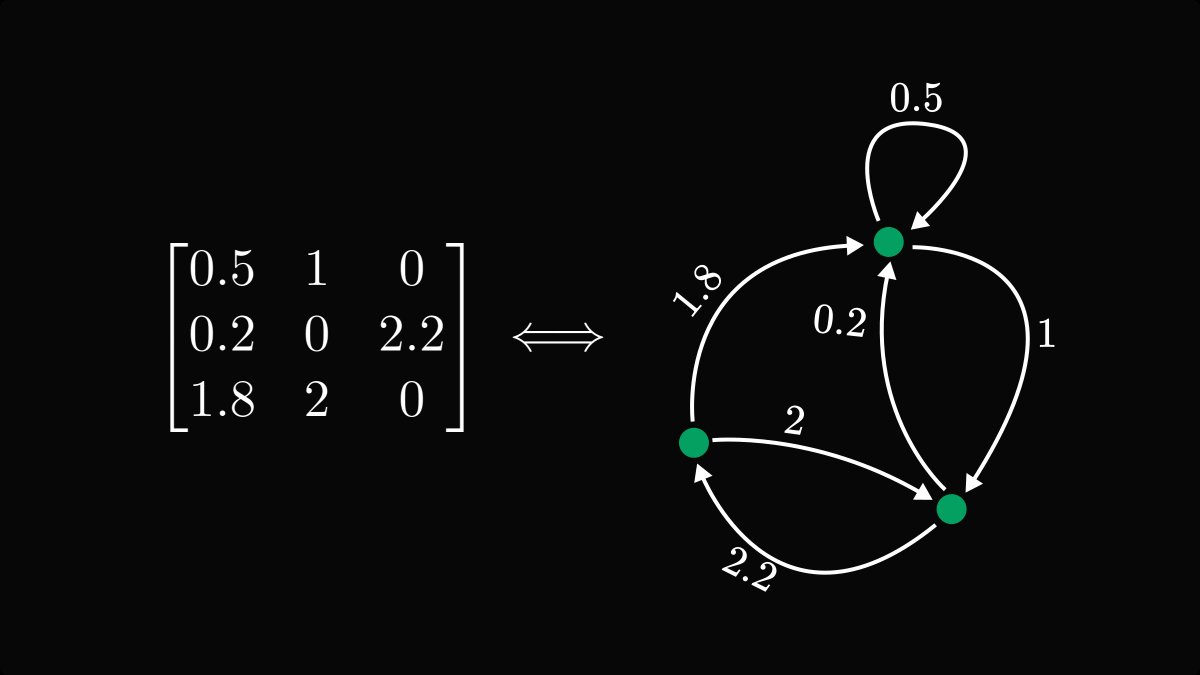
By stripping away all unnecessary details, we end up with a few nodes connected by edges. This was the first graph.

After getting rid of the noise, we can listen to the signal. This way, Euler discovered a simple criteria that solved his problem: to traverse all edges exactly once in a single walk, either

• all nodes must have even edges,
• or all nodes must have even edges except two.

Since all five nodes of Königsberg's graph have an odd number of edges, we cannot cross each bridge exactly once.

And so, graph theory was born.

Abstraction is one of the strengths of scientific thinking. By trimming unnecessary features, we obtain models that can fit to a wide array of problems.

Without abstraction, our tools would be extremely limited.

Graph theory has fruitful applications in the study of

• data structures and databases,
• computer networks and security,
• sociology,
• molecular interactions,
• biochemical pathways,

and much more. Graph theory came a long way from a mathematical puzzle.

Having a deep understanding of math will make you a better engineer. I want to help you with this, so I am writing a comprehensive book about the subject.

If you are interested in the mathematics of machine learning, check out the early access!

tivadardanka.com/book