Thread by @s_scardapane

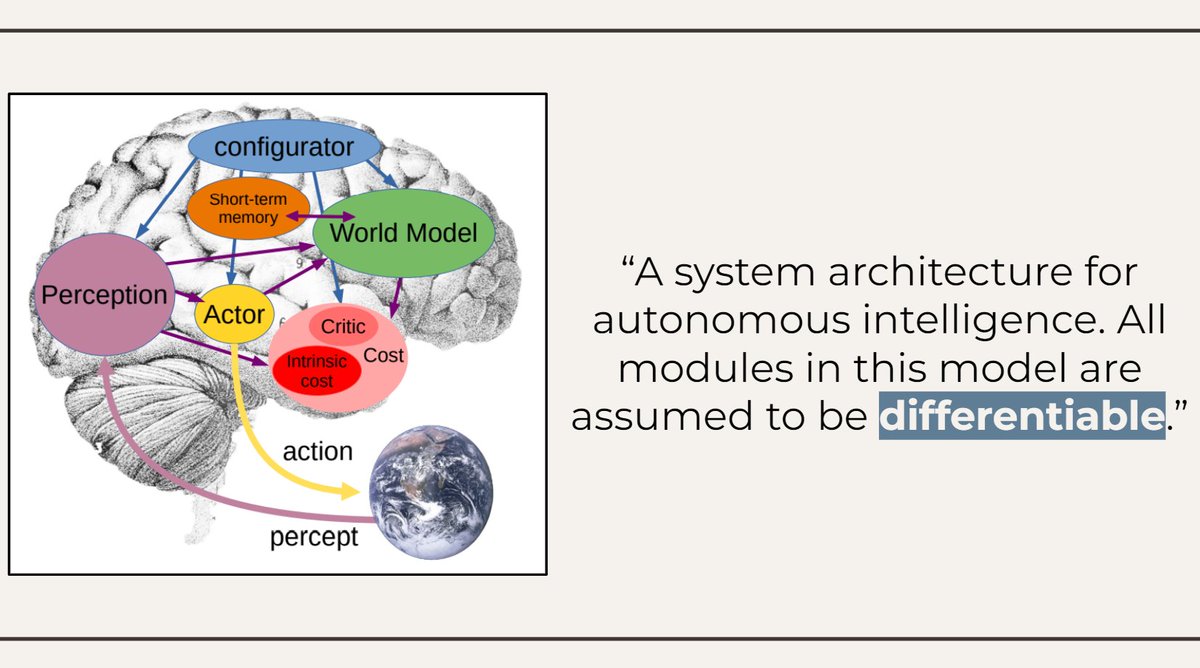
*Generative Flow Networks*

A new method to sample structured objects (eg, graphs, sets) with a formulation inspired to the state space of reinforcement learning.

I have collected a few key ideas and pointers below if you are interested. 👀

1/n

👇

*Flow Network based Generative Models for Non-Iterative Diverse Candidate Generation*
#NeurIPS paper by @folinoid @JainMoksh et al. introducing the method.

The task is learning to sample objects that can be built 1 piece at a time ("lego-style").

2/n

arxiv.org/abs/2106.04399

For example: a complex molecule can be built by adding one atom at a time; an image by colouring one pixel per iteration; etc.

If you formalize this process, you get a state space where you move from an "empty" object to a complete object by traversing a graph.

3/n

The only thing you have is a reward function describing how good each object (eg, protein) is.

GFlowNets understand this reward as a flow of water running through the graph: the flow you get at the terminal nodes is the reward of the corresponding object.

4/n

Under this interpretation, you train a neural network to predict how the flow goes through the graph, by imposing that the incoming and outgoing flows at each node are conserved.

With this, you get one consistency equation per node that you can enforce with a loss function.

5/n

The network trained in this way (GFlowNet) is enough to solve your original problem: by traversing the graph with probabilities proportional to the flow, you sample objects proportionally to their reward!

6/n

*GFlowNet Foundations*

Now you can move to this mammoth paper by @TristanDeleu @edwardjhu @mo_tiwari @folinoid

They show GFlowNets can be extended in many ways, notably, to sample conditional paths or to compute entropies and other quantities.

7/n

arxiv.org/abs/2111.09266

*Trajectory Balance: Improved Credit Assignment in GFlowNets*

Building on it, @JainMoksh @folinoid @ChenSun92 et al. show a much better training criterion by sampling entire trajectories, making training significantly faster.

8/n

arxiv.org/abs/2201.13259

*Bayesian Structure Learning with Generative Flow Networks*
by @TristanDeleu @AntGois @ChrisEmezue @SimonLacosteJ

Moving to applications, here they leverage GFlowNets to get state-of-the-art results in learning the structure of Bayesian networks.

9/n

arxiv.org/abs/2202.13903

*Biological Sequence Design with GFlowNets*
@bonadossou @JainMoksh @alexhdezgcia @folinoid @Mila_Quebec

Another cool application: the design of biological sequences with specific characteristics (I admit I am a little bit out of my depth here).

10/n

arxiv.org/abs/2203.04115

*GFlowNets for Discrete Probabilistic Modeling*
@alex_volokhova

The basic GFlowNet assumes your reward function is given, but you can also train it jointly using ideas from energy-based modelling. In this work, they use it to generate images.

11/n

arxiv.org/abs/2202.01361

Yoshua Bengio wrote about GFlowNets: "I have rarely been as enthusiastic about a new research direction", that "creative juices are boiling", and about "bridging the gap between SOTA AI and human intelligence".

More hype on AI, yay! 🤷‍♂️

12/n

yoshuabengio.org/2022/03/05/gen…

A few final pointers:

- Blog post on the original paper: folinoid.com/w/gflownet/
- A tutorial on Notion: milayb.notion.site/GFlowNet-Tutor…
- The original code: github.com/GFNOrg/gflownet

Let me know if I missed anything interesting!