
We started #Week11 of #VisualAlgebra with a new diagram of one of the isomorphism theorems. I made this over spring break. The concept is due to Douglas Hofstadter (author of "Gödel, Escher, Bach"), who calls this a "pizza diagram".
1/14 Mon 🧵👇
1/14 Mon 🧵👇

Though we constructed semidirect products visually last week, we haven't yet seen the algebraic definition. On Friday, we saw inner automorphisms, which was the last step we needed.
Recall the analogy for A⋊B:
A = automorphism, B = "balloon".
2/14 M

Recall the analogy for A⋊B:
A = automorphism, B = "balloon".
2/14 M


Next, we asked when a group G is isomorphic to a direct product or semidirect product of its subgroups, N & H.
Here are two examples of groups that we are very familiar with.
3/14 M

Here are two examples of groups that we are very familiar with.
3/14 M


Say that subgroups N,K are LATTICE CONJUGATES if
1. G = NK, and
2. N∩K={e}.
This has a very nice interpretation in terms of subgroup lattices! (Recall: NH is only a subgroup if one of N & H normalizers the other. Or weaker: one of them is normal.)
4/14 M
1. G = NK, and
2. N∩K={e}.
This has a very nice interpretation in terms of subgroup lattices! (Recall: NH is only a subgroup if one of N & H normalizers the other. Or weaker: one of them is normal.)
4/14 M
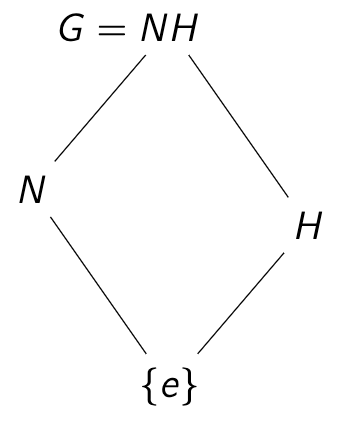
Suppose N,H are subgroups of G. We proved the following.
Thm 1: G≅N×H iff N & H are lattice conjugates, and BOTH normal.
Thm 2: G≅N⋊H iff N & H are lattice conjugates, and N is normal.
This is easy to check in the subgroup lattice by inspection!
5/14 M
Thm 1: G≅N×H iff N & H are lattice conjugates, and BOTH normal.
Thm 2: G≅N⋊H iff N & H are lattice conjugates, and N is normal.
This is easy to check in the subgroup lattice by inspection!
5/14 M
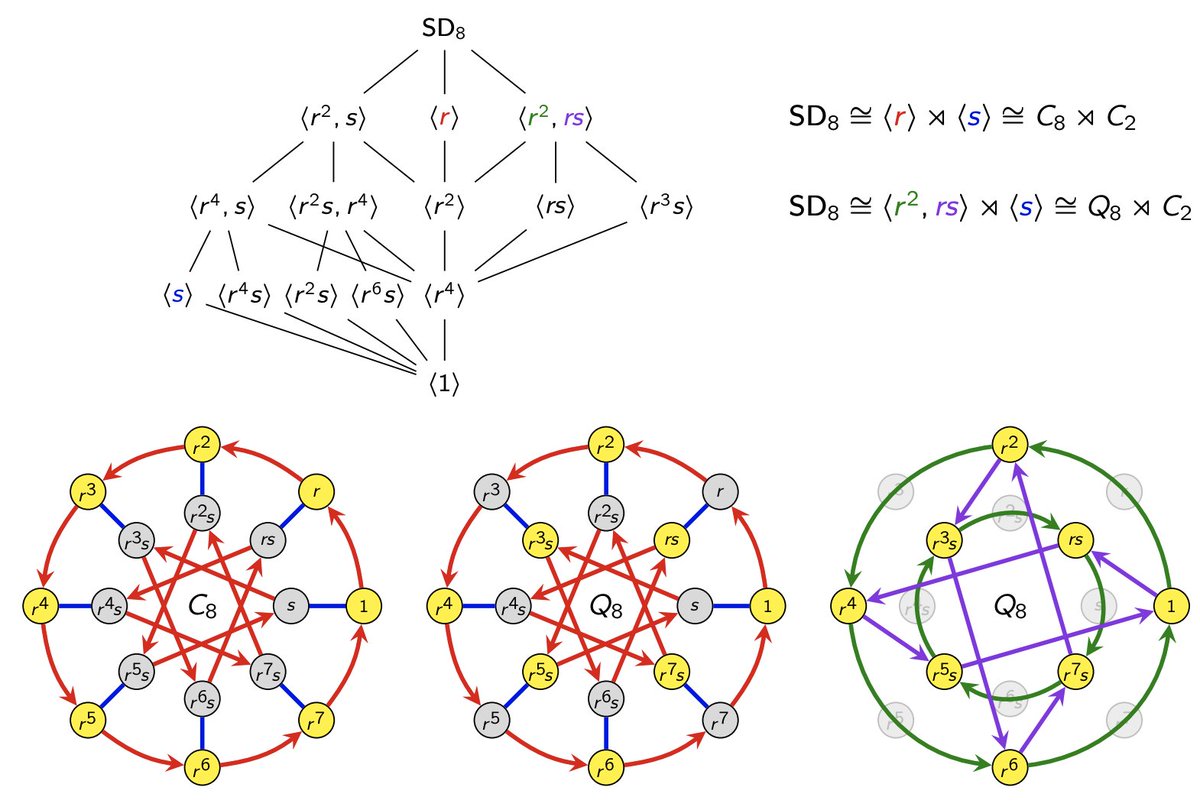
Here's an example. The semidihedral group SD_8 breaks up into a non-trivial semidirect product of two of its subgroups, two different ways.
We can see this by inspection, both in its subgroup lattice (see the lattice conjugates?) and in its Cayley diagrams.
6/14 M
We can see this by inspection, both in its subgroup lattice (see the lattice conjugates?) and in its Cayley diagrams.
6/14 M
Here's a non-example. Recall the generalized quaternion group Q_{32} = <ζ_{16}, j>, where r=ζ_{16} = e^{2πi/16}. Note how every nontrivial cyclic subgroup contains r^8=-1.
Q_{32}, and more generally, Q_{2^n}, is NOT a (nontrivial) semidirect product of two subgroups.
7/14 M
Q_{32}, and more generally, Q_{2^n}, is NOT a (nontrivial) semidirect product of two subgroups.
7/14 M

I like this example a lot. The dihedral group D_6 is isomorphic to a direct product, D_3×C_2, and a semidirect product C_6⋊C_2. The Cayley diagrams are shown on the right. Do you see each pair of lattice conjugates in the subgroup lattice?
And that's all for Chapter 4!
8/14 M
And that's all for Chapter 4!
8/14 M

Next up, Chapter 5: Group Actions. Let's go back to the first week, and recall the difference b/w a GROUP of ACTIONS, and the SET of CONFIGURATIONS it permutes.
9/14 M
9/14 M

Notice how there was a bijection b/w actions and configurations.
In this section, we'll drop this requirement. In doing so, we'll get "action diagrams", that are generalizations of Cayley diagrams.
But how do we just drop this requirement? Can you think of an example?
10/14 M
In this section, we'll drop this requirement. In doing so, we'll get "action diagrams", that are generalizations of Cayley diagrams.
But how do we just drop this requirement? Can you think of an example?
10/14 M

Here's one! My "favorite example" of a basic action, and it embodies many properties that we'll see throughout this chapter.
I struggled mightily with group actions as a student. MOST STUDENTS DO, THIS IS NORMAL.
The algebraic definition is just so weird & unmotivated.
11/14 M
I struggled mightily with group actions as a student. MOST STUDENTS DO, THIS IS NORMAL.
The algebraic definition is just so weird & unmotivated.
11/14 M

Of course, if you'd asked me as a student if I understood actions, I'd have said "yes", "I think so", or "pretty much".
Looking back, I really didn't. I think EVERYONE who has studied math can in some way relate to this feeling.
Here's how I explain group actions now.
12/14 M
Looking back, I really didn't. I think EVERYONE who has studied math can in some way relate to this feeling.
Here's how I explain group actions now.
12/14 M

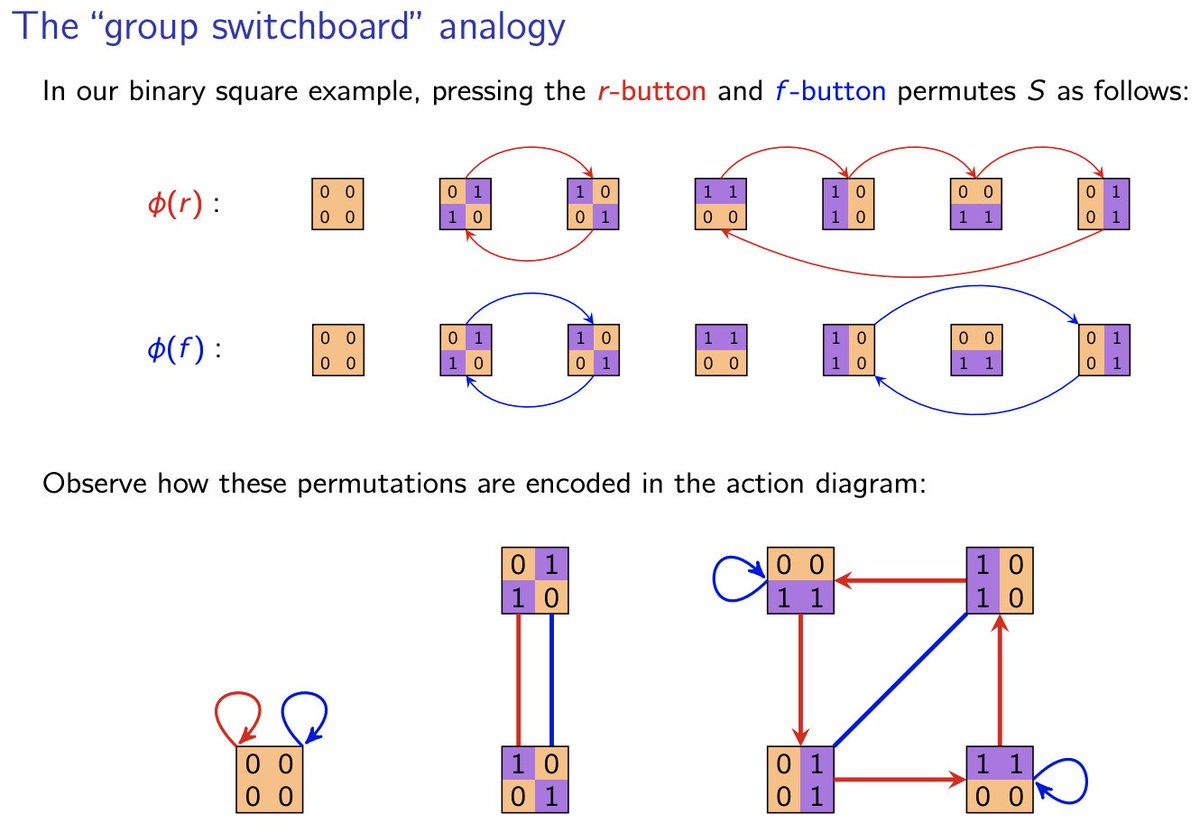
Formal definition: a group G acts on a set S if there is a homomorphism
φ:G-->Perm(S)
to the set of permutations of S.
φ(g) = "the permutation that results by pressing the g-button". That's it!
13/14 M
φ:G-->Perm(S)
to the set of permutations of S.
φ(g) = "the permutation that results by pressing the g-button". That's it!
13/14 M
Compare that to the unmotivated, classic algebraic definition. Instructors are the "gatekeeper" of this mysterious concept, which isn't appreciated by most students.
Our fun w/ group actions is only getting started. Stay tuned for classic concepts revealed in new ways!
14/14 M
Our fun w/ group actions is only getting started. Stay tuned for classic concepts revealed in new ways!
14/14 M

We started out Wednesday with three standard examples of group actions involving D_4. We've seen pictures like these earlier, but only now that we've defined group actions can we speak of them in the proper framework.
1/9 Wed 🧵👆👇
1/9 Wed 🧵👆👇

Every action has FIVE FUNDAMENTAL FEATURES.
Three "local" properties, of individual set or group elements. (today)
Two "global" properties, of the action (homomorphism) φ:G→Perm(S). (Friday)
We'll soon see a certain duality relating pairs of these.
2/9 W
Three "local" properties, of individual set or group elements. (today)
Two "global" properties, of the action (homomorphism) φ:G→Perm(S). (Friday)
We'll soon see a certain duality relating pairs of these.
2/9 W

The 3rd local feature isn't always emphasized as much in a class as orb(s) and stab(s) are, but it's important, and is in some sense "dual" to the latter. We'll see what I mean by "dual" via a "fixed point table".
Note: I write LOCAL features in lowercase.
3/9 W
Note: I write LOCAL features in lowercase.
3/9 W

I strongly recommend thinking about these features, first and foremost, using our "group switchboard analogy" from #Week10.
It makes the proofs straightforward, like that stab(s) is a subgroup. We talked it through in terms of switchboards, but the proof is left for HW.
4/9 W

It makes the proofs straightforward, like that stab(s) is a subgroup. We talked it through in terms of switchboards, but the proof is left for HW.
4/9 W


Let's return to my favorite example.
Key observation: the BIGGER an orbit gets, the FEWER paths loop back. So the stabilizers are SMALLER.
Notice how |stab(s)|*|orb(s)|=|D_4|=8 in each case.
WHERE HAVE WE SEEN THIS BEFORE?!?!
5/9 W
Key observation: the BIGGER an orbit gets, the FEWER paths loop back. So the stabilizers are SMALLER.
Notice how |stab(s)|*|orb(s)|=|D_4|=8 in each case.
WHERE HAVE WE SEEN THIS BEFORE?!?!
5/9 W

The "ah-ha's" were quite audible at this moment. Remember this; I've been hammering it home for over a month:
The INDEX of N(H) is the SIZE of cl(H).
The INDEX of C(g) is the SIZE of cl(g).
Both of these are special cases of a more general result about group actions!
6/9 W

The INDEX of N(H) is the SIZE of cl(H).
The INDEX of C(g) is the SIZE of cl(g).
Both of these are special cases of a more general result about group actions!
6/9 W


I had skipped the proofs of both of these (only did a sketch of one, left the other for HW) because the proof of the more general result (the orbit-stabilizer theorem, which we'll see on Friday), is completely analogous.
7/9 W
7/9 W

Here's a key concept, I call it a "fixed point table". I think it should be self-explanatory.
Notice how the stabilizers and fixed point sets are "dual" to each other: one can be read off the columns, and the other off the rows.
We're going to revisit this table!
8/9 W

Notice how the stabilizers and fixed point sets are "dual" to each other: one can be read off the columns, and the other off the rows.
We're going to revisit this table!
8/9 W


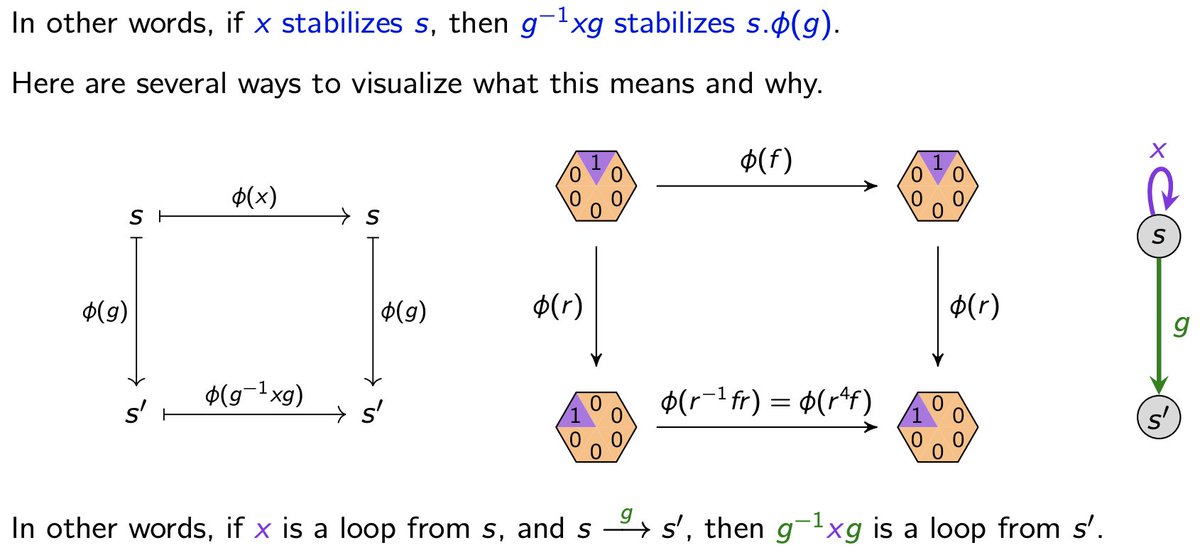
Note that elements in the same orbit might have different stabilizers, but not "too different". In fact, any two stabilizers must be conjugate subgroups. This picture illustrates why. I LOVE the simple "loop" interpretation on the right.
On Friday: the 2 global features!
9/9 W
On Friday: the 2 global features!
9/9 W
• • •
Missing some Tweet in this thread? You can try to
force a refresh


































