Thread by @VisualAlgebra

Finishing up our🧵👇 #VisualAlgebra class in #Week15 with divisibility and factorization. I'm a little short on visuals, but here are two really nice ones on what we'll be covering, made by @linguanumerate.

Henceforth, we'll assume that R is an integral domain.

1/8 Mon

The integers have nice properties that we usually take for granted:

--multiplication commutes
--there aren't zero divisors
--every nonzero number can be factored into primes
--any 2 nonzero numbers have a unique gcd and lcm
--the Euclidean algorithm can compute these

2/8 M

Some, but not all of these hold in general integral domains. This is what we'd like understand!

If b=ac, we say "a divides b", or "b is a multiple of a".

If a | b and b | a, they're "associates", written a~b.

HW: a~b iff they differ by a unit (i.e., a=bu).

3/8 M

We say:

b∉U(R) is "irreducible" if its only divisors are units and associates.

p∉U(R) is "prime" if p | ab ⇒ p | a or p | b.

In the integers, these agree. But in other integral domains, we only have prime ⇒ irreducible.

4/8 M

Things can get even weirder -- the length of different factorizations need not be the same.

For example, in R=Z[x^2, x^3]:

x^6 = x^2 * x^2 * x^2 = x^3 * x^3.

Note that x^2 is not prime because x^2 | x^3 * x^3, but x^2 ∤ x^3 in R.

5/8 M

Fortunately, there's a type of ring where such "bad things" don't happen.

An ideal I generated by a single element I=(a) is a "principal ideal".

An int. domain where every ideal is principal is a principal ideal domain (PID).

Examples include Z, F, F[x] (field F).

6/8 M

We'll see soon that in a PID:

--gcd's and lcm's exist
--irreducible ⇒ prime
--every element (nonzero, nonunit) can be uniquely factored into primes.

Exercise: use the division algorithm to show that in Z, every ideal is principal, generated by its smallest non-zero elt.

7/8 M

Let a,b∈R.

We call d the "greatest common divisor" of a & b if c | d, for all other common divisors c.

We call m the "least common multiple" of a & b if m | n, for all other common multiples n.

Next time, we'll see why these always exist in a PID.

8/8 M

We started Wednesday by proving that in a PID, any two non-zero numbers have a GCD, and left the similar proof of the LCM for the HW.

Then we showed that in a PID, irreducible ⇒ prime.

Cor: Z[√-5] is not a PID! (Scroll up: 3 is irreducible but not prime.)

1/6 Wed 🧵☝️👇

The proof that a PID is a UFD uses the fact that PIDs are Noetherian (exercise). If factorization failed, then we could create an infinite ascending chain of ideals. Due to time, I only sketched the idea of the proof.

2/6 W

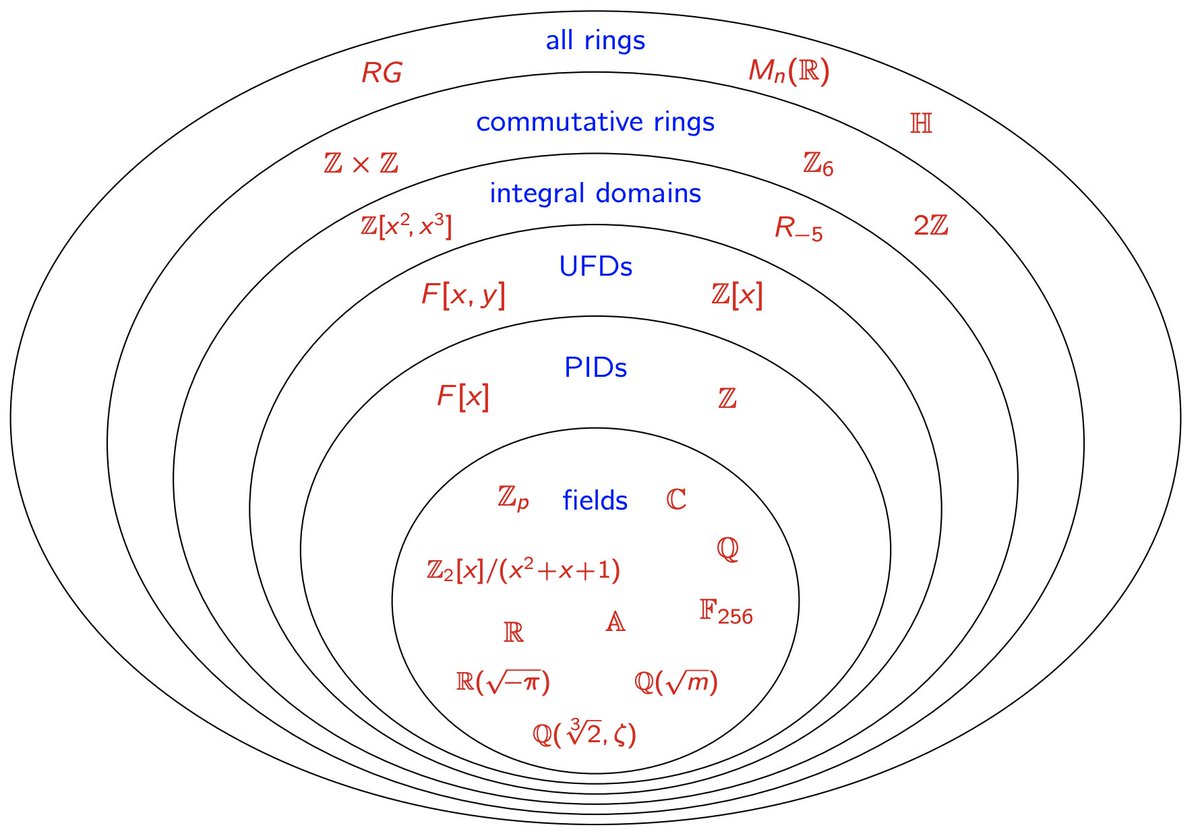
Here is a summary of the types of rings that we've seen thus far, how they're related, and examples. We'll add to this on Friday.

3/6 W

In most intro to proofs class, students learn about the Euclidean algorithm, and how it can be used to find gcd(a,b).

Let's warm up with an example.

4/6 W

Though GCDs exist in a PID, there need not be a Euclidean algorithm to construct them.

Such an algorithm requires a "degree function", which can be thought of as

--absolute value in Z
--deg(f(x)) in F[x]

5/6 W

See the formal definition below.

On Friday (last day of class!), we'll prove some basic properties of Euclidean domains, see some examples & non-examples, especially involving the "algebraic integers", and some open questions.

Almost at the finish line, stay with us!

6/6 W