Thread by @Yuhu_ai_

After showing a few examples, large language models can translate natural language mathematical statements into formal specifications.

We autoformalize 4K theorems as new data to train our neural theorem prover, achieving SOTA on miniF2F!

1/

Paper: arxiv.org/abs/2205.12615

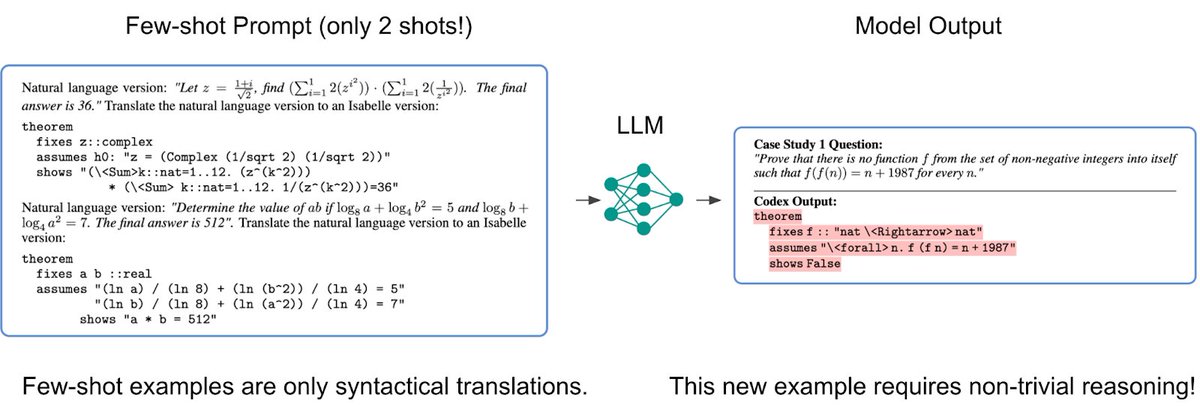
We show two randomly chosen few-shot examples in the prompt, from latex to formal math (Isabelle). Note that these two examples are merely examples of syntactical translations, without much sophistication in reasoning or natural language understanding.

2/

Now, let the examples do the talking!
See the figure attached – Codex perfectly formalizes an IMO problem! It handles the negation “there is no function” by proof-by-contradiction. It understands the phrase “into itself” and correctly formalizes the co-domain of f.

The next figure shows a perfect translation of a grade school math problem by PaLM. This is remarkable because such a statement is completely out-of-distribution – no formal mathematicians are interested in formalizing grade school math problems ;)

4/

Let’s also look at a failure case as well – in this case Codex fails to formalize the concept of “linear function”. It made up a name: linear f.

5/

Can the model learn to formalize such problems if the prompt contains an example that explains the concept? We find if we add a tangentially related problem, then the model can formalize the “linear function” perfectly!

6/

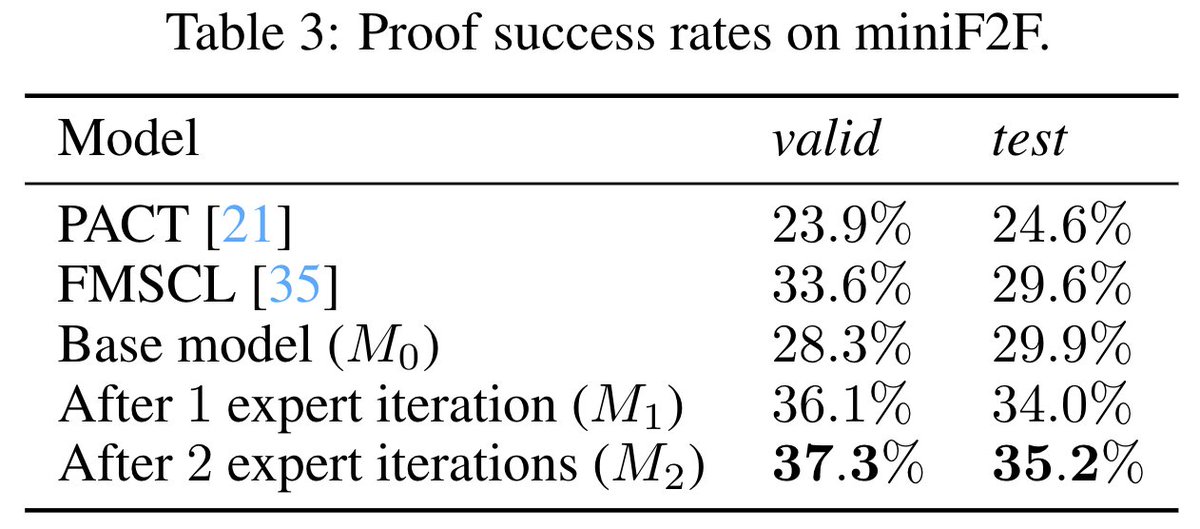
We use Codex to formalize 3908 MATH problems. We then run expert iteration on these autoformalized statements. This allows us to achieve a new state of the art on the miniF2F theorem proving benchmark.

This is the first proof-of-concept of practical autoformalization!

7/

We further explore if the model can handle more advanced mathematics beyond competition problems. We find these models are surprisingly good at turning formal statements into natural language as well!

8/

We see the model makes a jump in reasoning. Going from the definition, "for all x, if x in A -> x in B", to a more concise and abstract phrase "A is a subset of B". Also the same for "finite intersections" and "arbitrary unions". See examples in the figures!

9/

Why is this surprising? People know large language models can turn natural language descriptions into code. However, the existing known successes are limited to commonly used programming languages (e.g., Python). Formalizing mathematics is different for at least two reasons.

10/

1. The formal math data is very scarce. The whole Isablle proof script is only about 180MB. 2. There is almost zero aligned data between natural language and formal mathematics, whereas docstrings for language like Python are broadly available.

Our finding hence shows a very surprising capability of these models. They learned very general and transferable knowledge that allows them to work with low-resource formal language.

12/

Lastly, big thanks to my collaborators: @AlbertQJiang, @WendaLi8, @MarkusNRabe, Charles Staats, @Mateja_Jamnik, @ChrSzegedy!!!