What do Lyapunov functions, offline RL, and energy based models have in common? Together, they can be used to provide long-horizon guarantees by "stabilizing" a system in high density regions! That's the idea behind Lyapunov Density Models: sites.google.com/berkeley.edu/l…
A thread:
A thread:

Basic question: if I learn a model (e.g., dynamics model for MPC, value function, BC policy) on data, will that model be accurate when I run it (e.g., to control my robot)? It might be wrong if I go out of distribution, LDMs aim to provide a constraint so they don't do this. 



By analogy (which we can make precise!) Lyapunov functions tell us how to stabilize around a point in space (i.e., x=0). What if we want is to stabilize in high density regions (i.e., p(s) >= eps). Both require considering long horizon outcomes though, so we can't just be greedy! 
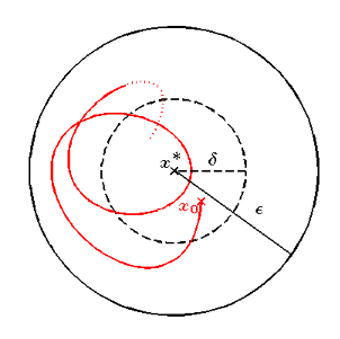
We can take actions that are high-density now, but lead to (inevitable) low density later, so just like the Lyapunov function needs to take the future into account, so does the Lyapunov dynamics model, integrating future outcomes via a Bellman equation just like in Q-learning.
LDM can be thought of as a "value function" with a funny backup, w/ (log) density as "reward" at the terminal states and using a "min" backup at other states (see equation below, E = -log P is the energy). In special cases, LDM can be Lyapunov, density model, and value function! 

Intuitively, the LDM learns to represent the worst-case future log density we will see if we take a particular action, and then obey the LDM constraint thereafter. Even with approximation error, we can prove that this keeps the system in-distribution, minimizing errors! 

Some results -- here, we use model-based RL (MPC, like in PETS) to control the hopper to hop to different locations, with the LDM providing a safety constraint. As we vary the threshold, the hopper stops falling, and if we tighten the constraint too much it stands in place. 

By @katie_kang_, Paula Gradu, Jason Choi, @michaeljanner, Claire Tomlin, and myself
web: sites.google.com/berkeley.edu/l…
paper: arxiv.org/abs/2206.10524
This will appear at #ICML2022!
web: sites.google.com/berkeley.edu/l…
paper: arxiv.org/abs/2206.10524
This will appear at #ICML2022!
• • •
Missing some Tweet in this thread? You can try to
force a refresh













