Thread by @CuriepolisBuch

~~ Etwas Interessantes: Wieso ist die Lichtgeschwindigkeit konstant? ~~

Dass die Lichtgeschwindigkeit sich von alltäglichen Geschwindigkeiten dadurch unterscheidet, dass sie nicht zunimmt, wenn man sich dem Lichtstrahl entgegen bewegt, wissen wir. Aber warum ist das so? 🧵

Viele Menschen denken, Michelson und Morley hätten mit ihrem Experiment, bei dem sie mithilfe eines Interferometers die Geschwindigkeit von auf der Erde eintreffendem Sternlicht untersuchten, gezeigt, dass diese sich nicht in Abhängigkeit von der Erdbahngeschwindigkeit ändert.

(In dem Sinne: Erde bewegt sich mit 30 km/s auf den Stern zu oder von ihm weg -- Lichtgeschwindigkeit in beiden Fällen identisch.)

Die Konstanz ergibt sich jedoch bereits aus den Gesetzen der Elektrizitätslehre, die James Clark Maxwell 20 Jahre vor dem MM-Experiment formulierte.

Diese Gleichungen sind Grundlage aller elektrischen Phänomene, aller Glühbirnen, Fahrraddynamos, Turbogeneratoren, Föhns, Toaster und Waschmaschinen.

(Elektronische Komponenten dagegen, z. B. Halbleiterdioden, können nur durch quantenmechanische Modelle erklärt werden.)

Auf den ersten Blick sehen diese Formeln ziemlich fremdartig aus -- nicht für den wissenschaftlichen Laien, der sich wundert, was denn diese Dreiecke und Kreuze meinen mögen, sondern auch für den Physikstudenten, für den sie meist die erste Berührung mit der Vektoranalysis sind..

...und diese nimmt sich häufig derart einschüchternd aus, dass er nach der Vorlesung noch etwas muckriger und übellauniger in die Mensa stiefelt als bei Physikstudenten allgemein üblich.

Die Vektoranalysis gilt als kopfzerbrechendes Feld, und die zugehörigen Übungsaufgaben als Wochenendenkiller. Das muss jedoch nicht so sein. Man kann sich dem Thema sehr gechillt nähern.

Das wichtigste Konzept, mit dem James Clark Maxwell die elektrischen Phänomene beschrieb, ist das des Feldes. (Manche behaupten, ihm sei diese Idee bei mystischer Meditation über den antiken Demeterkult gekommen: falls wahr, wäre dies cool.)

Ein Feld ist ganz einfach eine Funktion, die jedem Ort im Raum einen oder mehrere Zahlenwerte zuordnet. Bei einem Wert nennt man das Feld auch Skalarfeld, es sieht dann z. B. so aus:

f(x, y, z) = sin(x*y)*z

(Oder irgendeine andere Funktion der drei Raumkoordinaten.)

Ein Beispiel wäre die Temperatur in Abhängigkeit vom Ort in einem Luftvolumen: zu jedem durch drei Koordinaten charakterisierten Ort gehört je ein Zahlenwert, eben die Temperatur.

Elektrische Phänomene haben jedoch nicht nur einen Betrag, sondern auch eine Richtung.

Deshalb werden sie mithilfe von Felder beschrieben, die jedem Ort *drei* Zahlenwerte zuordnen, e.g.:

f(x, y, z) = (sin(x*y*z) ; cos(2*z) ; 4*sin(x)*cos(y))

Dies nennt man ein Vektorfeld. Man kann die drei Werte als Länge eines Pfeils in x-, y- und z-Richtung deuten.

Man stellt sich also vor, dass man an jeden Raumpunkt (x, y, z) einen kleinen Pfeil anklebt, dessen Länge in x-Richtung von dem ersten Wert -- hier: sin(x*y*z) --, in y-Richtung von dem zweiten -- hier: cos(2*z) -- angegeben wird, ebenso entsprechend für die z-Richtung.

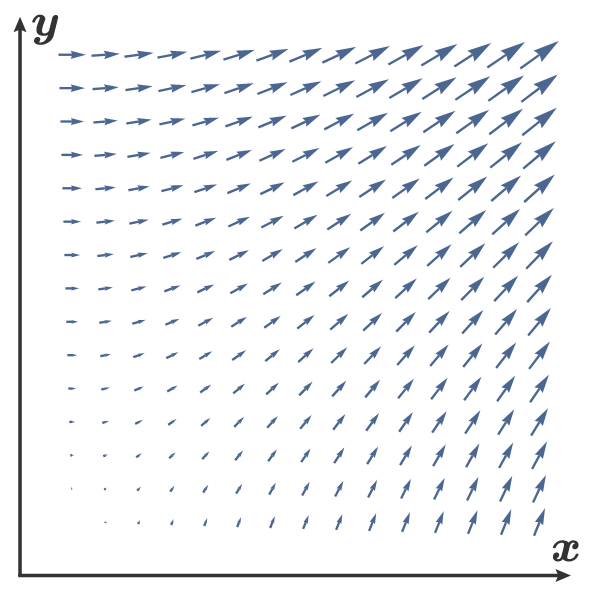
(Das Bild zeigt ein zweidimensionales Beispiel.)

Warum Vektorfelder für die Elektrizitätslehre so geeignet sind, sieht man sofort, wenn man einen Hufeisenmagneten unter ein Blatt Papier legt und Eisenspäne darauf streut.

Offensichtlich hat das Feld überall eine Stärke und eine Richtung.

Man kann sich das Eisenspanmuster aus vielen kleinen Pfeilen zusammengesetzt denken. Je stärker das Feld an einem Ort ist, desto länger ist der Pfeil.

Alle elektrischen Phänomene beruhen darauf, dass in der Natur eine Eigenschaft existiert, die man Ladung nennt. Objekte können positive oder negative Ladung haben. Geladene Objekte üben Kräfte aufeinander aus. Die Max. Gl. beschreiben diese Kräfte mittels zweier Vektorfelder...

...dem elektrischen Feld (E) und dem magnetischen (B).

Das elektrische Feld eines geladenen Objekts zieht andere geladene Objekte direkt darauf zu, wenn die Ladungen unterschiedliches Vorzeichen haben, oder stößt sie radial fort, wenn sie gleiches Vorzeichen aufweisen.

Das magnetische Feld dagegen geht von sich bewegenden Ladungen aus. Beispielsweise bildet sich um einen Draht, durch den Ladungen fließen, ein ringförmiges Magnetfeld, wie man hier wieder anhand von Eisenspänen sieht.

Das Feld von Hufeisenmagneten u.ä. beruht auf mikroskopischen Ladungsbewegungen in den Hüllen der Atome.

Magnetfelder üben auf ruhende Ladungen überhaupt keine, auf sich bewegende eine seitlich wirkende Kraft aus, wodurch diese eine Korkenzieherbahn beschreiben.

Man sagt oft, dass dies der wichtigste Unterschied zur Schwerkraft sei: diese wirke immer radial (+ anziehend) und nie seitlich -- dies stimmt allerdings nicht, es gibt auch eine "gravimagnetische" Kraft, die von rotierenden Massen ausgeht und angezogene Objekte seitlich ablenkt.

Bei der Erde ist der Gravimagnetismus jedoch extrem schwach (wenn auch mit modernem Equipment messbar), bei kompakten Objekten wie Schwarzen Löchern wird sie beträchtlich. Doch dies ist eine andere Geschichte, die ein andermal erzählt werden soll.

Die Maxwell-Gleichungen sagen nun, wie die beiden Feldarten erzeugt werden können. Um dies quantitativ zu formulieren, braucht es die beiden Symbole auf der linken Seite: das Dreieck und das Kreuz.

Was sie bedeuten, kann man in Worten ganz einfach formulieren:

Dreieck Feld = Divergenz des Feldes = wie stark strömt es aus einem bestimmten Punkt hervor?

Dreieck Kreuz Feld = Rotation des Feldes = wie stark ist es an einem bestimmten Punkt verwirbelt?

Das Dreieck nennt man "Nabla" nach einem antiken Musikinstrument, das oft im Alten Testament erwähnt wird.

Man veranschaulicht sich elektrische und magnetische Felder oft mit Feldlinien. Diese sind eine gute visuelle Metapher für die Struktur des Feldes. Sie verlaufen parallel zu den Pfeilen ("Vektoren), und liegen umso näher beisammen, je stärker das Feld ist.

Mittels des Feldlinienmodells lassen sich Divergenz und Rotation besonders leicht verstehen.

Man denkt sich um den Punkt, für den man sich interessiert, einen Würfel, der relativ zum Gesamtfeld sehr klein ist (also z. B. 0.1 mm Kantenlänge bei einem üblichen Hufeisenmagneten)...

...und dann ist die Differenz aus der Zahl an Feldlinien, die aus dem Würfel herauskommen und der Zahl derer, die hineingehen, die Divergenz an diesem Punkt.

Wenn man die Feldlinien als Strömungslinien auffasst -- das sind die Wege, die Objekte, die in einer Strömung schwimmen, bechreiben; z. B. Blätter auf einem Fluss: dann gibt die Rotation an, wie stark und in welche Richtung die Blätter sich an einem bestimmten Punkt drehen.

Es genügt zum Verständnis, sich zu merken:
~~ Nabla "Feld" = wie stark kommt es hervor?
~~ Nabla kreuz "Feld" = wie stark wirbelt es?

Wenn man sich das klargemacht hat, ist man den Studenten, die nach der ersten Elektrodynamikvorlesung übellaunig zur Mensa trippeln, weit voraus!

Dann kann man die Maxwell-Gleichungen ganz einfach lesen:

Wie stark kommt das elektrische Feld aus einem Punkt hervor: so stark, wie die Ladungsdichte an diesem Punkt geteilt durch die Naturkonstante Epsilon Null.

Wie stark kommt das magnetische Feld hervor: gar nicht.

Anschaulich meint das, dass elektrische Feldlinien von geladenen Objekten ausgehen, magnetische dagegen immer im Kreis verlaufen. Dies ist jedoch noch nicht ganz sicher, da es möglich ist, dass es auch magnetische Ladungen gibt -- "Monopole" -- die noch nicht entdeckt wurden.

(Man sollte also strenggenommen schreiben:
Divergenz B = ?.)

Die beiden weiteren Gleichungen sind für die Elektrotechnik besonders wichtig, da sie beschreiben, wie elektrische und magnetische Felder auseinander hervorgehen:

Wie stark wirbelt das elektrische Feld: so stark wie die zeitliche Änderung des Magnetfeldes mal -1.

Hierauf beruhen Generatoren und Dynamomaschinen: Eine Drahtspule rotiert in einem Magnetfeld -- so dass dieses sich zeitlich ändert und dadurch in dem Draht ein elektrischer Feldkreis entsteht und der Strom fließt.

Letzte Gleichung:

Wie stark wirbelt das magnetische Feld: so stark, wie elektrischer Strom durch den fraglichen Punkt fließt (J) plus Konstante Epsilon Null mal zeitliche Änderung des elektrischen Feldes -- beides zusammen mal Konstante My Null.

Auf diesem letzten Gesetz beruht die Erzeugung von Magnetfelder durch Ströme: z. B. ringförmig um einen Draht oder mittels einer Spule.

Worin der Clou besteht, sieht man, wenn man die letzten beiden Gleichungen zusammensieht:

~~ Verwirbelung des elektrischen Feldes hängt ab von zeitlicher Änderung des Magnetfeldes;

~~ Verwirbelung des Magnetfelds hängt ab von zeitlicher Änderung des elektrischen Feldes.

Denn dies bedeutet ja notwendigerweise, dass sich zeitlich ändernde Magnetfelder sich ändernde elektrische Felder hervorrufen können und diese sich ändernde Magnetfelder und diese wiederum...! So dass ein ganzer Zopf von elektrischen und magnetischen Felder entsteht.

Mit einigen kleinen Rechenregeln lassen sich die beiden Gleichungen vereinen. Man erhält folgenden Ausdruck. In Worten:

Wie stark ändert sich die räumliche Änderungsrate des elektrischen Feldes: so stark, wie sich die zeitliche Änderungsrate ändert mal beiden Konstanten.

Was bedeutet "Änderung der Änderungsrate"?

Dies entspricht der Krümmung einer Straße: je stärker sie gekrümmt ist, desto weiter muss ein Autofahrer, der sie entlangfährt, das Lenkrad einschlagen.

Räumliche Krümmung der Feldstärke = beide Konstanten mal zeitliche Krümmung.

Wenn man schon von eingeschlagenen Lenkrädern und Krümmungen hört, dann ahnt man, worauf das Ganze hinausläuft: ein gekrümmtes Ding -- eine Wellenbewegung!

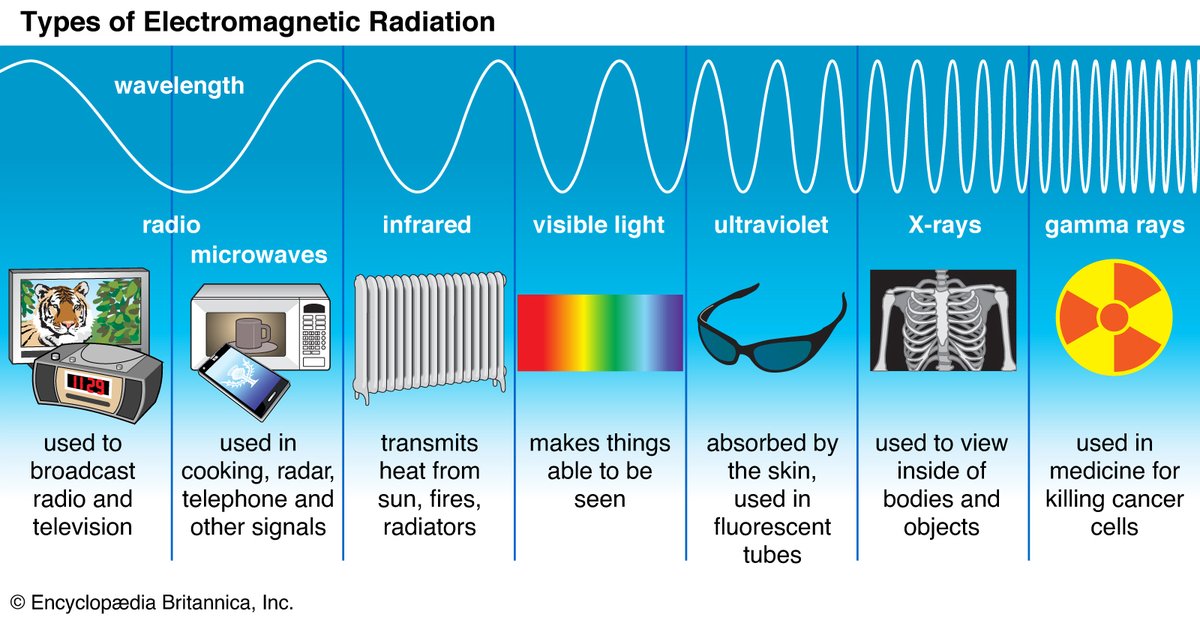
Die Gleichung sagt: sich ändernde elektrische und magnetische Felder bilden Wellen, die sich mit der Gechwindigkeit c = SQRT(1 / Epsilon Null x My Null) ausbreiten.

Lichtwellen sind elektromagnetische Wellen mit Wellenlängen (Abstand Maximum zu Maximum) zwischen 400 und 800 Nanometern (Milliardstel Meter = 10⁻⁹ m); aber auch Radiowellen, Wärmestrahlung, UV, Röntgen- und Gammastrahlung gehören dazu.

Und die Ausbreitungsgeschwindigkeit c hängt nur vom Produkt zweier Naturkonstanten ab -- nicht etwa vom Bewegungszustand des Beobachters! Das Ergebnis von Michelson und Morley, das Grundlage der Speziellen Relativitätstheorie ist, folgt also bereits aus der Elektrizitätslehre.

Zum Schluss ein feiner, kleiner Fakt, den die breite Mehrheit der studierten Physiker (einschließlich habilitierte!) erfahrungsgemäß nicht kennt.

Man kann mehrere Schwingungen aufaddieren, so dass ein Signal beliebiger Form entsteht: dies nennt man Fourieranalyse...

-- so entstehen beispielsweise aus vielen überlagerten Sinusschwingungen in einem Radiosender Stimmen, Musik, etc.

Physiker, die *meinen*, Ahnung zu haben, sagen nun: einzelne Schwingungen in dem Wellenpaket können sich mit Geschwindigkeiten größer als c ausbreiten...

...das Paket als Ganzes hat aber immer die Geschwindigkeit c.

FALSCH.

Auch das Paket kann sich u. U. schneller als c bewegen.

Was sich dagegen immer mit c ausbreitet, ist die Vorderfront des Paketes -- genauer gesagt, der Anstieg an Feldstärke, der mindestens nötig ist, um 1 Bit Information zu übertragen.

Wenn man also liest: "Elektromagnetische Strahlung hat im Vakuum immer die Geschwindigkeit c = 3 x 10⁸ m/s", dann ist gemeint:
Die minimale Änderung an elektrischer oder magnetischer Feldstärke, die nötig ist, um 1 Bit zu übertragen, hat im Vakuum immer diese Geschwindigkeit! 😎

@threadreaderapp unroll