Thread by @BachmannRudi

Vorlesung 11, Makro, PhD: heute lernen wir, warum man manchmal die dritte Ableitung der Nutzenfunktion braucht, und was Dynamisches Programmieren ist.

Das letzte Mal hatten wir fuer eine ganz spezielle Kombination aus Nutzenfunktion (CARA, constant absolute risk aversion) und Einkommensprozess (random walk mit normalverteilten Schocks) analytisch den optimalen Konsumprozess hergeleitet: einen random walk mit Drift.

Dabei stellt gerade der Drift-Term ein Mass fuer das Vorsichtssparen dar, das sich gegenueber einer quadratischen Nutzenfunktion ergibt, in der die Haushalte risikoneutral sind. Heute lernen wir, was genau an dem Beispiel Vorsichtssparen erzeugt.

Es ist die Tatsache, dass die dritte Ableitung bei CARA Nutzenfunktionen strikt positiv ist (ebenso wie bei den meisten anderen Nutzenfunktionen, die man so verwendet, zB CRRA). Dritte Ableitung der Nutzenfunktion > 0 bedeutet, dass der Grenznutzen nicht nur fallend, sondern

strikt konvex fallend ist. Fuer strikt konvexe Funktionen gelten nun zwei wichtige mathematische Eigenschaften:

1) Es gilt Jensens Ungleichung, das heisst der Durchschnitt der Funktionswerte ist hoeher als der Funktionswert des Durchschnitts.

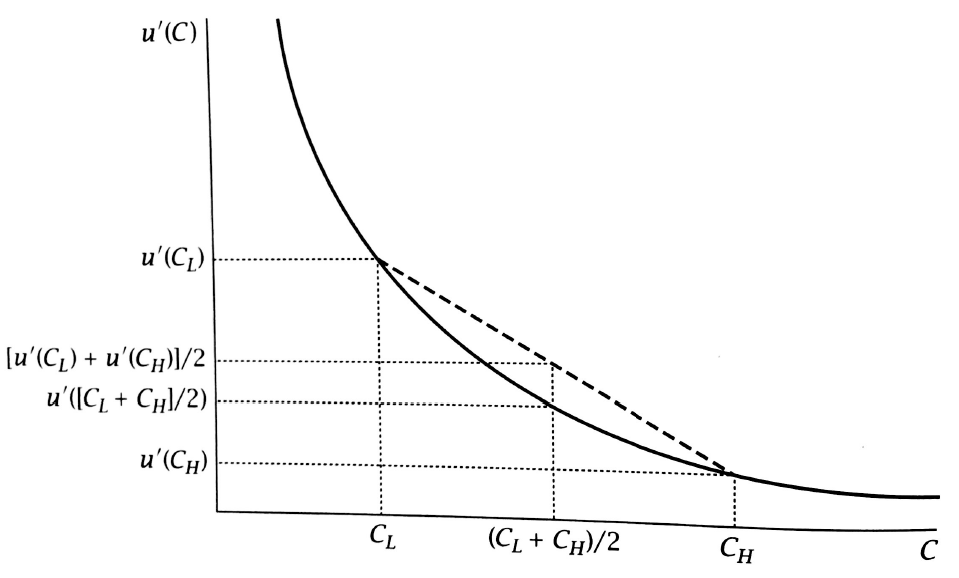
2) Ein sogenannter mean-preserving spread, also eine erwartungswerterhaltende hoehere Varianz in der Konsumunsicherheit, fuehrt zu einem hoeheren durchschnittlichen Grenznutzen.

Aus beiden Eigenschaften und der Eulergleichung kann man nun ableiten, dass der Konsum heute immer niedriger ist als bei certainty equivalence, also wenn man sich um Konsumrisiko morgen ueberhaupt nicht schert. Diese Differenz nennt sich Vorsichtssparen.

Harter Schnitt. Dynamisches Programmieren. Das ist ein methodischer Einschub in die Vorlesung, in dem wir zunaechst einmal eine weitere Methode lernen, die Eulergleichung abzuleiten. Das ist aber nur ein paedagogisches Zwischenziel, denn schliesslich koennen wir das ja schon:

Bei Sicherheit machen wir das mit dem Lagrange-Ansatz, bei Unsicherheit haben wir ein Variationsargument bemueht (spaeter werden wir sehen, dass man das aber auch mit dem Lagrangeansatz loesen kann mit etwas Kreativitaet).

Das tolle am Dynamischen Programmieren ist, dass es formal nahezu gleich funktioniert, ob die Welt nun sicher oder unsicher ist.

Der Trick besteht darin, ein unendliches Maximierungsproblem (in dem man eine unendliche diskontierte Summe von flow benefit Funktionen maximiert) in eine Zweiperiodenmaximierungsproblem umzuschreiben.

Nebenbemerkung: das funktioniert zwar auch bei einem endlichen Maximierungsproblem, aber die Power vom Dynamischen Programmieren wird erst bei einem unendlichen Maximierungsproblem so richtig deutlich.

Die Grundidee, das Optimalitaetsprinzip, geht auf den Mathematiker Bellman zurueck: das Optimum laesst sich so finden, dass man heute unter der Annahme maximiert, dass man sich von morgen an auch wieder optimal verhalten wird.

Beispiel: wenn man von South Bend nach Minneapolis fahren will und das auf einer optimalen Route und man muss durch Chicago (wegen des Michigan Sees), dann kann man das Problem auch dadurch loesen, dass man erst die optimale Route von South Bend nach Chicago berechnet und dann

von Chicago nach Minneapolis. Das Ergebnis einer solchen Ueberlegung ist, dass man statt einer unendlichen Sequenz von optimalen Konsumwahlen, die optimale Loesung durch zwei Funktionen kennzeichnet, die den Zustand der Welt in die optimale (Konsum)wahl abbildet, was man die

Politikfunktion (policy function) nennt, die aber nix mit Politik zu tun hat, sondern Zustaende der Welt in optimales Verhalten abbildet. Daraus resultiert dann die sogenannte Wertfunktion (value function), die die Zustaende der Welt in den Wert optimalen Verhaltens abbildet.

Als Endprodukt des Dynamischen Programmierens will man diese beiden Funktionen finden (was wir bisher noch nicht so ohne weiteres konnten). Was wir heute allerdings erst gemacht haben ist zu zeigen, dass man mit Dynamischem Programmieren auch die Eulergleichung ableiten kann.

Das ist in der Tat nicht so trivial, dazu muss man in der Bedingung erster Ordnung, die aus der sogenannten Bellmangleichung folgt, die Ableitung der unbekannten Wertfunktion mit der Ableitung der bekannten flow benefit Funktion ersetzen koennen.

Das geht nur unter bestimmten Bedingungen. Fuer unser Konsum-Spar-Problem geht das aber. Fuer Kenner: die Beneviste-Scheinkman Formel gilt.

Das naechste Mal lernen wir dann, wie man aus der Bellmangleichung oder der Eulergleichung Politik- und Wertfunktion berechnen kann.

PS: es heisst natuerlich Benveniste-Scheinkman