Thread by @genkuroki

#Julia言語 以下のリンク先と同じことをやってみたい人のための解説

①まず、 julialang.org/downloads/ からCurrent stable releaseで自分のパソコンに合っているものをダウンロードし、自分のパソコンにインストールする。

②インストールしたJuliaを起動する。

添付画像はnightly build。続く

https://twitter.com/genkuroki/status/1575402345055522816

#Julia言語

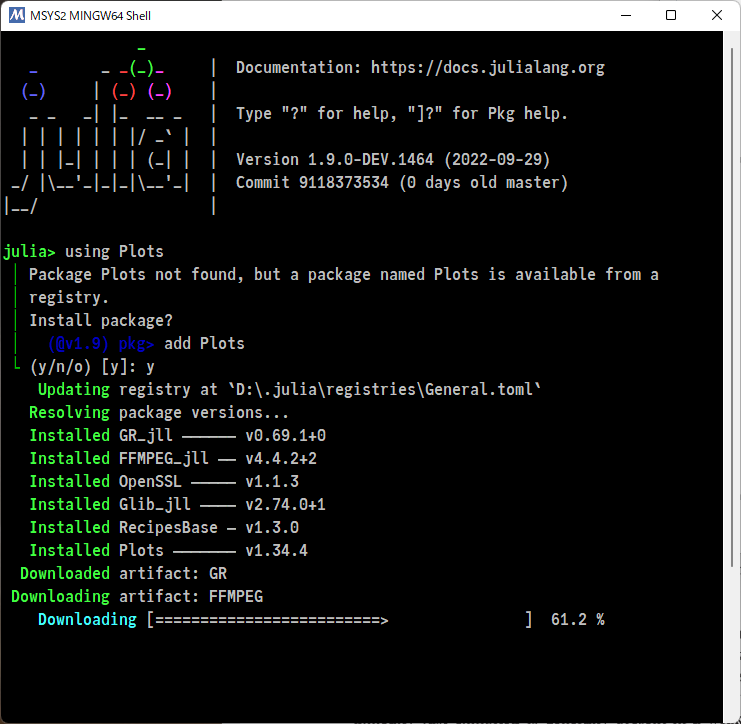
③添付画像1のように julia> プロンプトに

using Plots

と入力してエンターキーを押します。

そして添付画像2のように y と入力しエンターキーを押します。

すると添付画像3,4のようにPlots.jlパッケージがインストールされます。

#Julia言語

④ github.com/genkuroki/publ… にアクセスし、そこの In[1] のusing Plots以外の部分を、julia> プロンプトの側にコピー＆ペーストして下さい。

そして、最終行の確定のためにエンターキーも押しておく。

そしてしばらく待ちます。

#Julia言語

⑤添付画像のようにグラフが表示されれば成功です！

⑥公式ドキュメントのページにアクセスする。

docs.julialang.org/en/v1/

すでに他言語でプログラムを書いたことのある人は

docs.julialang.org/en/v1/manual/p…

を優先的に読むと時間の無駄を防ぎ易いと思います。

#Julia言語 私と同じような環境を使いたければ

nbviewer.jupyter.org/github/genkuro…

を参照。

https://twitter.com/genkuroki/status/1108053602457653248?s=20&t=vmAOSzsbA_76pJlqBPxrRw

#Julia言語 「超高級電卓」としてもJulia言語は便利に使えるのでインストールしておいて損がないようにも思えます。

#Julia言語 新しいもの好きならば、

(a->a[a.∉(a*a',)])(2:100)

を実行すると、どうして素数の配列が得られるか、について調べてみるとよいと思います。

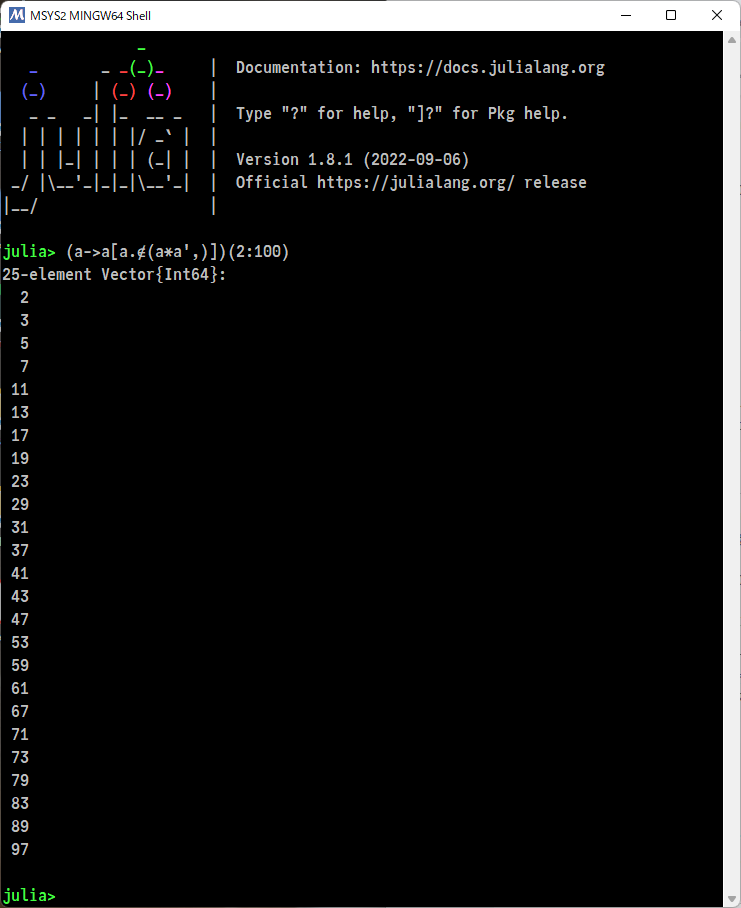
#Julia言語 (a->a[a.∉(a*a',)])(2:100) の謎解きをするには部分的に少しずつ実行して、結果を確認するとよいです。

添付画像
①a = 2:100
②b = a*a'

a*a'で 2×2から100×100までのかけ算の表が得られます。

#Julia言語

∉の入力の仕方は、julia> プロンプトで ? キーを押してヘルプモードにしてから、そこに ∉ をコピー＆ペーストしてエンターキーを押せばわかります。

\notin タブキー で入力できる。

#Julia言語 以上で紹介したように公式バイナリで ∉ のようなユニコード文字の入力方法がサポートされており、世界中のJuliaユーザーたちがユニコード文字を自分が書いたプログラムの中で利用しています。

c = a.∉(a*a',) とすると、素数番目の成分がtrue (1と表示されている)の配列が得られる。

#Julia言語 素数番目と書いたが2,3,4,...と2が最初。

.∉は∉のブロードキャストで、(a*a',)と( ,)でa*a'を囲んでいるのはブロードキャストからa*a'を保護するためです。Ref(a*a')も同じ目的のために慣用的に使われています。この部分が初めてだと難しいはず。

a[c]の結果は以下のようになります。

#Julia言語 a=2:100とa*a' に戻る。

a=2:100は2,3,4,...,100が縦に並んだ縦ベクトル扱いされます。

a'はその転置で横ベクトル扱いになります。

a*a'は縦ベクトル×横ベクトルなので行列になります。その行列が2×2から100×100までのかけ算の表になっていることは行列について知っていればわかる。

#Julia言語

17 ∉ a*a' は{2,3,...,100}中の2つの数の積の表に17が含まれていないので、true になります。

91 ∉ a*a' は19が含まれているのでfalseになる。

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10] .∉ (a*a',) は [1, 2, ..., 10]の各々の成分に以上の操作を施すこと(ブロードキャスト)を意味する。

#Julia言語 このブロードキャストは非常に便利で、理解しているとコードをものすごく簡略化できます。

ここに慣れると非常に快適にJuliaを超高級電卓として利用できるようになります。

#Julia言語

f(x, y) = x^2*y/(x^2+y^2)
x = y = range(-1, 1, 1001)
using Plots
surface(x, y, f)

と入力すると(添付画像1)、添付画像2のようなグラフが得られます。

これは原点で偏微分可能だが微分不可能な函数の有名な例になっています。