Thread by @genkuroki

#統計 以前にも述べたことですが、

ism.ac.jp/editsec/toukei…
情報量規準 AIC の統計科学に果たしてきた役割
小西 貞則
2019

の添付画像の部分はひどいです。

BICもあるKL情報量(+モデルによらない定数)の(大胆な)推定値になっていることを小西さんは理解していないっぽい。

リンクに続く

https://twitter.com/umaruyama/status/1329745143591706624

#統計 続き

以前に述べていたことは以下のリンク先すれっどにある。

BICは対数周辺尤度の-2倍の大胆な近似とみなされ、対数周辺尤度の-1倍の標本の確率的揺らぎに関する期待値は

　あるKL情報量+モデルによらないある定数

に一致している。

渡辺澄夫『ベイズ統計の理論と方法』を参照。

https://twitter.com/genkuroki/status/1329803252385210369

#統計 渡辺澄夫『ベイズ統計の理論と方法』のようなよく普及している教科書レベルの内容を理解していれば、【納得いきます】とは言ってはいけない案件。

その本に書いてあるように、BICの近似先の対数周辺尤度の-2倍は2KL情報量+定数の推定値だとみなされるので、情報量規準という呼び方は自然。

https://twitter.com/btreetaiji/status/1329768584059359234

#統計 「対数周辺尤度の期待値」という発想をできるかどうかが分かれ目になる。

その発想から自然にKL情報量+定数が出て来る。

順番に説明すれば大学1年生でも理解できそうな非常に易しい話。

対数周辺尤度のLaplace近似についても説明できればBICは簡単に出て来る。

#統計 「主義に基く統計学」に頭が染まっていると「対数周辺尤度の期待値」を考えることが阻害されそう。

難易度的に大学1年レベルの話題でこういうことになってしまうのは多分そういうことなのだと思う。

「ベイズ主義では真の分布を考えない」のようなことを平気で言えてしまう人達は要注意。

#統計 伝わったようですが、続く

https://twitter.com/btreetaiji/status/1575862258089222144

#統計 続き。主義に基く統計学に気を使うことが大事なことであるかのように振る舞うことは、ひどく不合理に見える。

2つ上のツイートで危惧していたことが現実の問題であることが示された。

https://twitter.com/btreetaiji/status/1575864752060141568

#統計 現代のP値の正しい使い方に関する専門的な議論は、ネイマン=ピアソンだとかフィッシャーの名前と「頻度論」「頻度主義」というような用語を出す議論からかなり遠く離れています。

そういう意味でも「頻度論」「頻度主義」という用語を使うときには要注意。

以下のスレッドを参照。

https://twitter.com/genkuroki/status/1575326237740138496

#統計 BICは対数周辺尤度の-2倍の大雑把な近似になっています。だから本質的に周辺尤度を見ていることになる。

周辺尤度も尤度なのでデータとモデル(事前分布を含む)の適合度の指標の1つとみなせる。

データとモデルがよくフィットしていても、それがオーバーフィッティングである危険性が常にある。

#統計 だから、尤度をモデル選択のための指標として使う場合にはオーバーフィッティングの問題に配慮する必要がある。

特にパラメータを尤度最大化(周辺尤度最大化を含む)で調節している場合には、パラメータ数を大きくするとオーバーフィッティングが起こり易い。続く

#統計 最尤法の予測分布の尤度をオーバーフィッティングのし易さで補正したものが、AIC(赤池情報量規準)。

ベイズ法で周辺尤度最大化で(ハイパー)パラメータを調節した場合に同様のことを行った結果がABIC。

ABICは(ハイパー)パラメータ数が0のとき、対数周辺尤度の-2倍になり、BICで近似される。

#統計 尤度は周辺尤度も含めて、モデルのデータの数値との適合度もしくは相性の良さの指標の1つに過ぎません。

尤度や周辺尤度が高い方が良いという考え方をしてはいけない。

こういう基本的な事柄と主義に基く統計学の相性は非常に悪いのです。

#統計 主義にこだわるダメなベイズの人は「周辺尤度最大化でハイパーパラメータを調節する経験ベイズは尤度原理を破るので使用禁止」のような滑稽なことを述べて、からかわれているようです。続く

#統計 しかし、赤池弘次さん達の仕事によって、オーバーフィッティングの可能性に配慮していれば、周辺尤度最大化によるパラメータの調節も現実における複雑な現象の統計分析法として有用であることがわかっています。

こういう歴史があるので、主義にこだわるのは滑稽だとわかっているわけです。

#統計 オーバーフィッティングに配慮したモデル選択のための適切な指標を用意しておけば、周辺尤度最大化による(ハイパー)パラメータの調節も役に立つことについては、小西さんの解説では以下の添付画像の部分にあります。

ism.ac.jp/editsec/toukei…

普通は、ピュア～な主義に殉じるために有用で優れた方法を捨て去りたいとは普通思わないので、普通に説明するときには、主義の話はする必要がないと思います。

主義の話は「主義に取り込まれないようにしようね！」という形式で別にするのが良いと思います。

#統計 小西さんの論説にはそういう尖った解説を期待していたのですが、BICの説明の部分で無用に「軟化」した態度になっているのを見て、がっかりしてしまいました。

そのせいで、BICもKL情報量+定数の(かなり大雑把な)推定値であるという一般読者にとって重要な情報が抜け落ちてしまっている。

#統計 赤池さんのAICやABICに関する仕事は、我々が知りたいことは「モデルとデータの数値の相性の良さ」そのものではないという点を明確化することに成功しました。

統計学ユーザーは、データの数値の背後に隠された大事な何かについて知りたいので統計学を使っています。

#統計 主義に基く統計学に取り込まれると、我々が本当に知りたいこととは別の「モデルとデータの数値の相性の良さ」に特別な価値があるかのように誤解することになり易いと思う。

その辺については以下のリンク先の解説を参照。

watanabe-www.math.dis.titech.ac.jp/users/swatanab…
小さな世界と大きな世界
渡辺澄夫

続く

#統計 続き

watanabe-www.math.dis.titech.ac.jp/users/swatanab…
「主義」を心配するみなさまへ
渡辺澄夫

「真の分布」の部分は「データの数値の背後に隠された大事な何か」に一般化した方が受け入れやすい説明になると思います。

#統計 例えば、薬Xとプラセボをそれぞれ与えたm人とn人がどれだけ重症になったかに関するデータがあったときに、我々が真に知りたいことは、そのデータの数値そのものではなく、薬Xには実際にどれだけ効き目があるかについてです。

データは偏っているだろうし、モデルも間違っているだろう。

多分その話は私によるこのスレッドへの反応です。

仮にそうならその話の解説を書いたのは私が先。

文脈を明瞭化するためにリンクをはってくれればうれしかった。

文脈を明瞭化することが都合が悪いと思ったのかな、とも思いました。

https://twitter.com/NozomiMaki2/status/1575950199939158016

#統計 ポイントを再度説明

①対数周辺尤度の-1倍の標本の確率的揺らぎに関する期待値はちょうどKL情報量+定数の形になる。

②対数周辺尤度の漸近挙動から、対数周辺尤度の実現値はその期待値のそう悪くない近似になることもわかる。

③対数周辺尤度の-2倍のLaplace近似でBICが得られる。

続く

#統計 続き

④以上によって、BICは

　サイズ0の標本から得られる
　サイズnの標本のモデル内予測分布の
　予測誤差+モデルによらない定数の点推定値の近似値

とみなされる。ただし予測誤差はKL情報量で測る。

#統計 BICは周辺尤度にLaplace近似を適用できる場合にしか使えない。モデルが正則である必要がある。WBICならモデルが正則でなくても使える。

#統計 AICやWAICは

　サイズnの標本から得られる予測分布の
　予測誤差の期待値+モデルによらない定数の点推定値

とみなされる。期待値はサイズnの標本の確率的揺らぎに関する期待値。予測誤差はKL情報量で測る。

期待値を取る前の予測誤差そのものとAICやWAICは逆相関しているので要注意。

#統計 この手の話題は、簡単な場合の具体的計算例を最初に見るようにしないと何も理解できないので要注意。

nbviewer.org/gist/genkuroki… には最もシンプルなベルヌイ分布モデルの場合のAIC, BIC, WAIC, LOOCV, 対数周辺尤度, WBICの計算例の詳細がある。

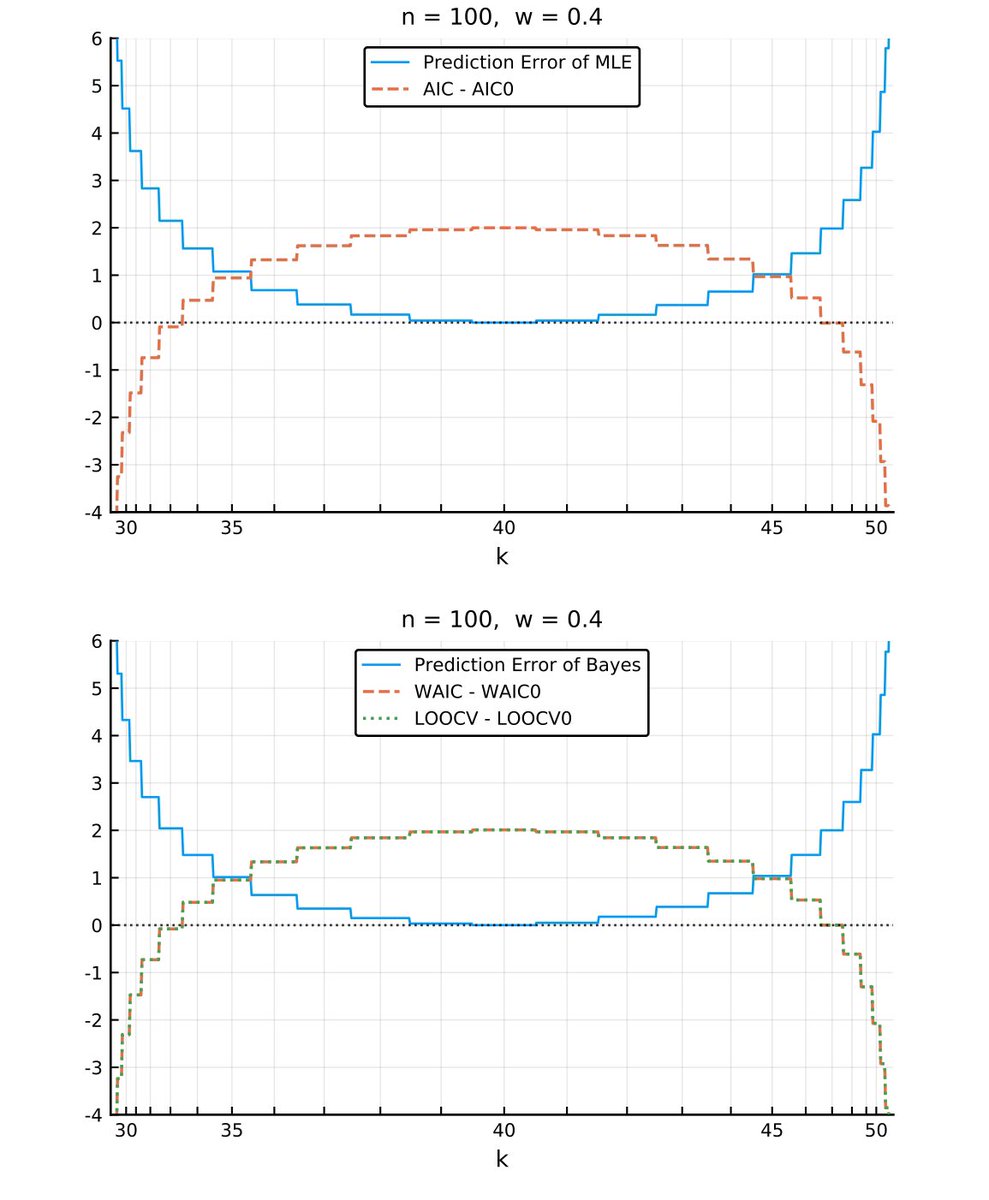
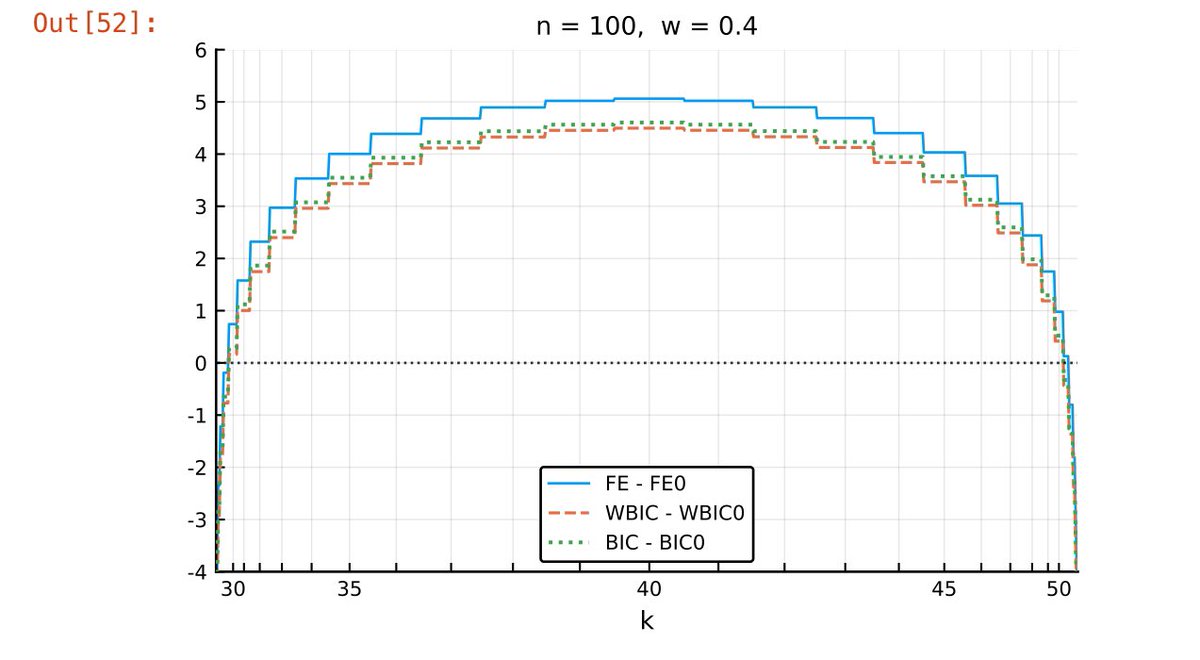
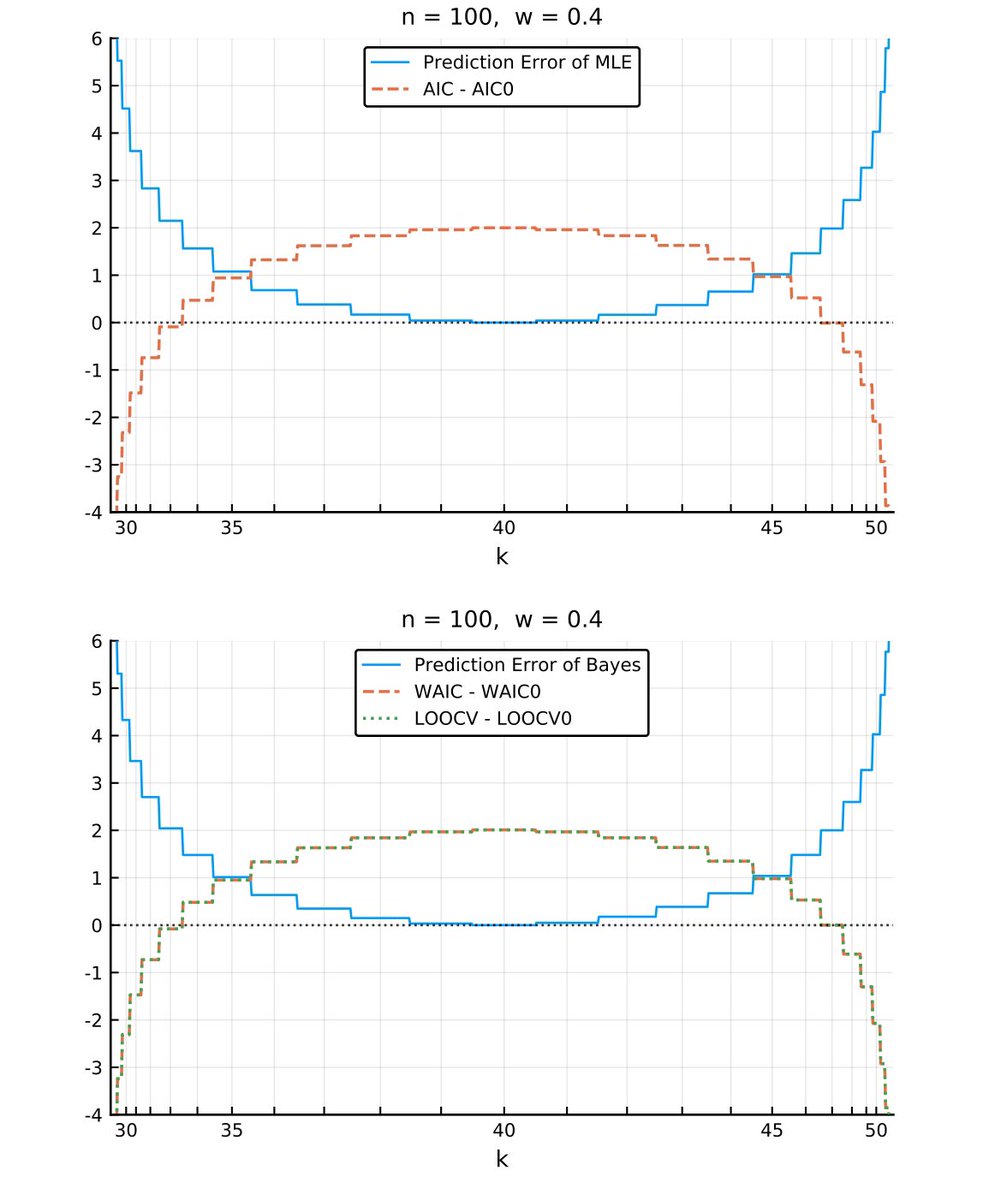
#統計 横軸は確率の大きさに比例するようにスケールしてある。確率スケールにしないと印象が全然違うグラフが得られるので注意！

以下のグラフを見れば、予測分布の予測誤差とAIC, WAIC, LOOCVが綺麗に逆相関していることがわかります。

この逆相関は普遍的に成立。

nbviewer.org/gist/genkuroki…