Thread by @genkuroki

#統計 P値や信頼区間に関する大学での講義は(数え切れないくらい強調していることですが)、論文 journals.sagepub.com/doi/10.1177/02… の内容(過信や自信過剰を引き起こさない考え方)に従うように改訂されるべきだと思います。

過去の大学の講義のほとんどがその意味では失格。

https://twitter.com/genkuroki/status/1619213870924713984

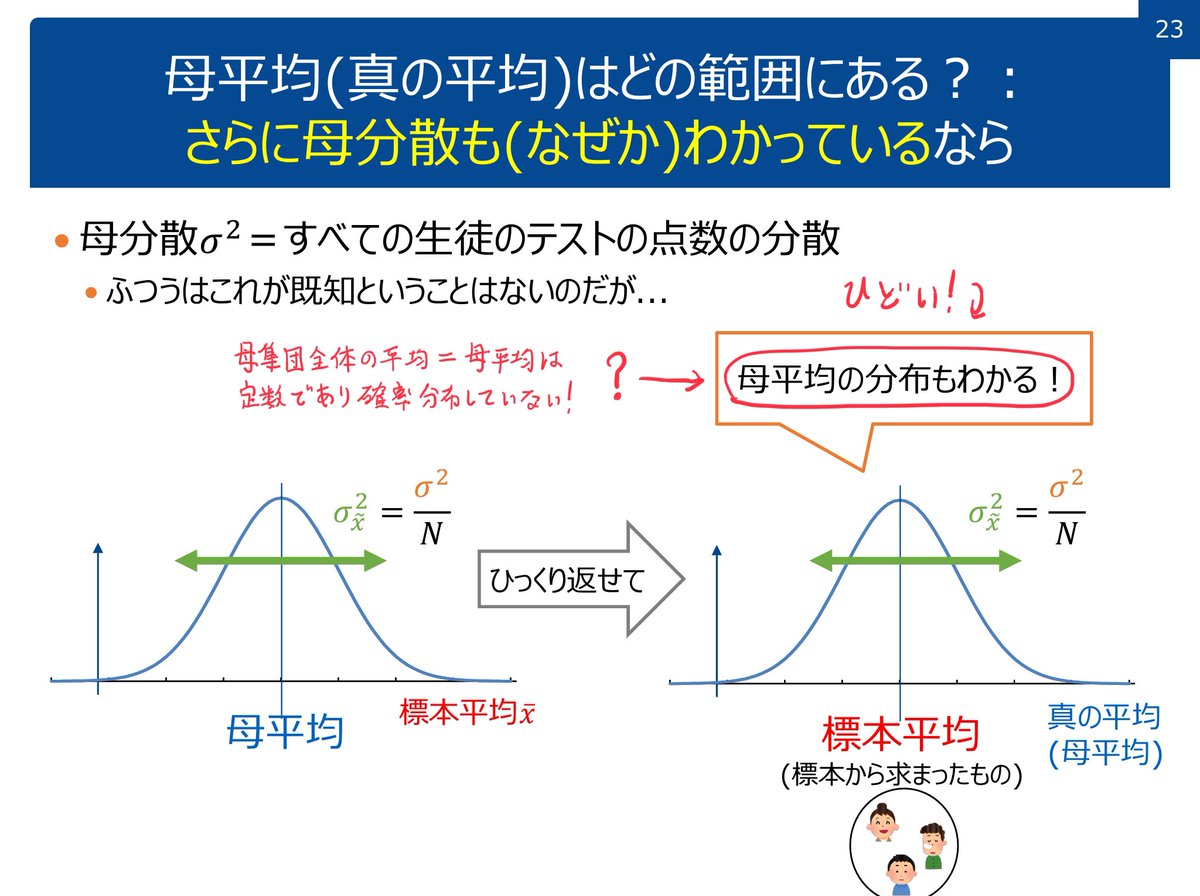
#統計 帰無仮説は統計モデルのパラメータの値に関する仮説になっており、P値を得るための確率の(近似)計算は帰無仮説下の統計モデル内で行うことになるので、統計モデルについての説明がない仮説検定の説明は最初から相手にする価値がないということになります。

#統計 仮説検定における「統計モデル」は「P値の計算に使われる数学的仮定の全体」のようにざくっと定義しておくと便利です。

例えば、P値の計算に確率の近似計算を使うならば、その近似がうまく行くという条件が統計モデルの中に含まれていると考えると便利。

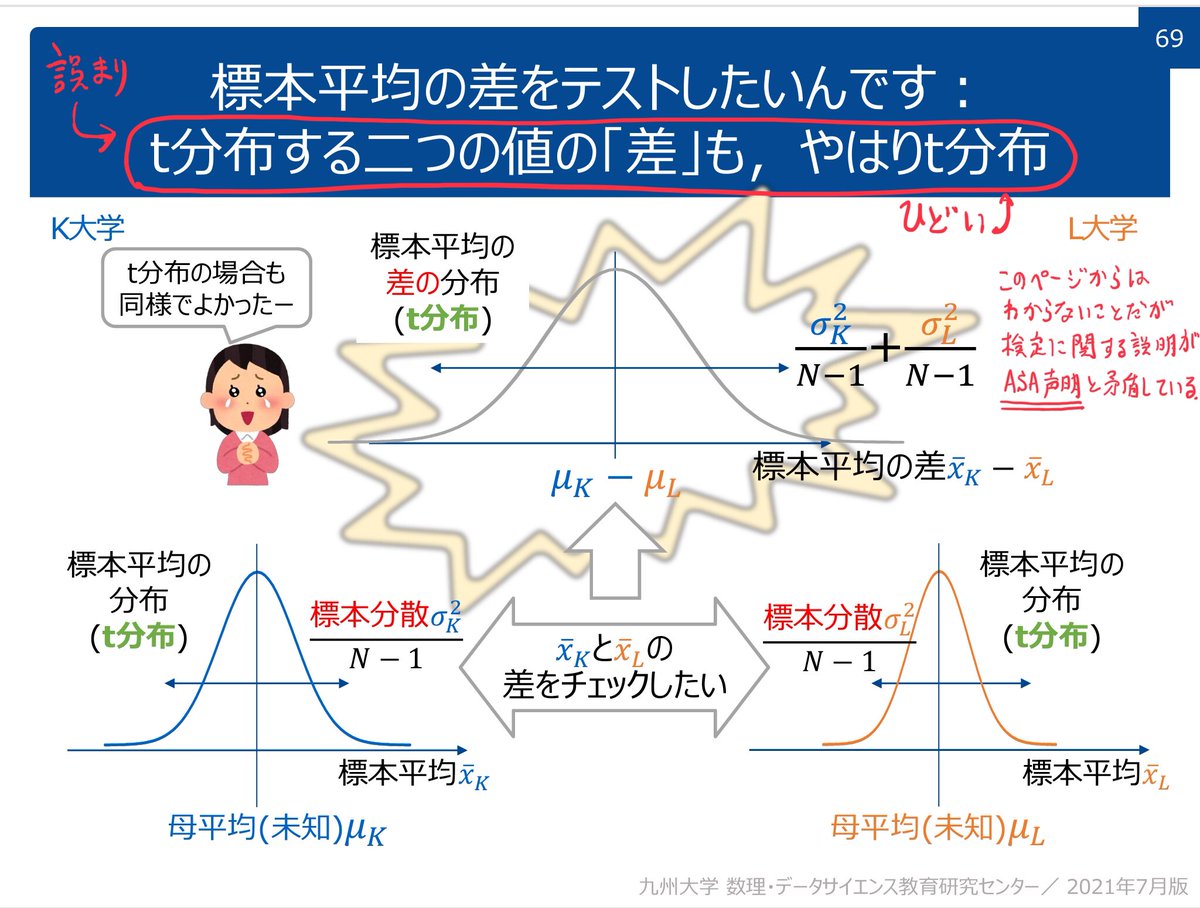
#統計 例えば、Welchのt検定で必要とされる数学的仮定を正確に言うことは結構難しいです。

「2群の母集団分布がともに正規分布になっていること」はWelchのt検定の統計モデルの説明として全然ダメ。

なぜならば、Welchのt検定は正規母集団の仮定が成立していなくても多くの場合に使用可能だから。

#統計 Wilcoxonの順位和検定のP値は「2群の分布が完全に等しい」というモデルの中で計算されます。

だから、2群の分布が左右対称で平均や中央値が互いに等しいとしても、分散や尖度が異なると、Wilcoxonの順位和検定では有意差が出易くなります。コンピュータで容易に確認可能です。続く

#統計 続き。2群の分布が左右対称で平均と分散が互いに等しいとしても、尖度が異なると、Wilcoxonの順位和検定では有意差が出易くなります。

分散が等しくてもWilcoxonの順位和検定では有意差が出易くなる場合があることはあまり知られていないと思います。続く

#統計 続き。そういう形で有意差が出易くなることは、Wilcoxonの順位和検定が適用される通常の状況では不適切です。

だから、Wilcoxonの順位和検定は無条件では使えない検定だということになります。

この辺も私は易しい話ではないと思います。

#統計 以上で述べたような易しくないことをある程度以上理解できた人だけが、Welchのt検定やWilcoxonの順位和検定を使う資格があります。

現実にはそういう資格がない人達がそれらの検定を使っており、特にWilcoxonの順位和検定は多くの場合に誤用されている疑いがあります。

#統計 さらにそれ以前の問題として、違いの適切な測り方についてほとんど何も考えずに「有意差を出せればなんでもよい」のように考えて、Welchのt検定とWilcoxonの順位和検定を同列に並べて比較すること自体に問題がありすぎます。

根本的におかしな考え方が蔓延している。

#統計 論文 journals.sagepub.com/doi/10.1177/02… を読んだ後に、現実の高等教育(大学と大学院)での統計学教育の現状について考えると、それらのギャップが非常に巨大であることがわかります。

みんなで少しでもまともな側に近付ける努力が必要。