Thread by @genkuroki

#統計

正確な説明にこだわっているようなのであえてコメント。

線形回帰でこだわるべき条件は「残差が正規分布」よりも「残差が独立同分布」の方です。

残差が非正規分布のi.i.d.のときの線形回帰は、非正規母集団のt検定と同じようにうまく行ったり、行かなかったりします。詳しい解説に続く。

https://twitter.com/shuntarooo3/status/1451809386830000130

#統計 例で説明します。

まず、残差がi.i.d.ではないが、残差全体は正規分布に従う場合があることの説明。

添付画像がそのような場合の例になっています。

データの散布図(青点達)を見ると、この場合には単純な線形回帰の適用が不適切であることは明らか。続き#

nbviewer.org/github/genkuro…

#統計 この例は回帰直線を2本にする必要があります。

1本の回帰直線に関する残差の値全体の分布は正規分布になります。

添付画像①から残差の分布がxへの依存性が分かる。

添付画像②はxを無視すると残差全体は正規分布になることの確認。(理論的にそうなることも確認済み)

続く

#統計 2本の回帰直線を使ったフィッティングの結果。

この場合に、データ全体の様子を見ずに、1本の回帰直線の残差の数値の分布だけを見ると「よし！正規分布になっているっぽい！大丈夫！」と誤解してひどいことになります。

残差が非正規分布のi.i.d.の場合の話に続く

#統計 残差が非正規分布のi.i.d.に従う場合は、観測されていない説明変数にyが非線形に依存している場合には起こり得ます。

そういう場合にも線形回帰の数学的仕組みは、nが十分大きいならうまく働いてくれる可能性が高い。

だから、「残差が正規分布」という条件を強調するのは厳密には誤り。続く

#統計 これは、中心極限定理によって、t検定を非正規母集団に適用しても多くの場合にうまく行くことの拡張になっている。

線形回帰でも、独立同分布な残差が正規分布に従っていなくても、拡張された中心極限定理によって、多くの場合にうまく行く。

こういうことは自分で数学的に考えれば分かる。

#統計 例で説明します。

添付画像①の非正規分布(期待値は0)」に独立に残差 uᵢ が従うと仮定します。

データは yᵢ = 1 + xᵢ + uᵢ で作る。

そのデータに通常の最小二乗法を適用すると添付画像②の結果が得られる。残差は全然正規分布に従っていないですが、回帰係数の推定はうまく行っている。

#統計 以上の設定で、データを大量に生成し、最小二乗法で求めた回帰係数達の値をプロットすると、添付画像のようになります。

その分布は、理論的にその分布が漸近する先の2変量正規分布でよく近似されていることもわかります。

ただしこれはn=1000の場合。

nが20だと誤差が見えるようになります。

#統計 n=20, 40, 100の場合

このように、i.i.d.の残差が正規分布に従っていなくても、最小二乗法で求めた回帰係数の分布は(拡張された)中心極限定理によって多変量正規分布で近似されるようになります。

#統計 以上では、xの1次函数への線形回帰(最小二乗法)を扱いましたが、xの非線形函数への線形回帰にも以上の結果はそのまま拡張されます。

別のスレッドでちょっと触れた「i.i.d.の直交射影に関する中心極限定理」に帰着できます。

#Julia言語 ソースコード
↓
nbviewer.org/github/genkuro…

#統計 以上で述べたことは、特別にそれについて書かれた文献を探さなくても、

中心極限定理を証明の粗筋込みで理解

していてかつ

最小二乗法が直交射影であることを理解

していれば、その場で自分で考えれば分かることです。

文献の権威に頼る必要はない。

#統計 関連スレッド

https://twitter.com/genkuroki/status/1626546122444660736

#統計 yがx₁とx₂に依存しているときに、yのデータをx₁だけに回帰すると、残差の分布がi.i.d.だが全然正規分布にならない場合
↓

https://twitter.com/genkuroki/status/1627237735730925568

#統計 もちろん、最尤法の漸近論を使ってもよいですが、線形回帰ごときでそれを使うと相対的に難しい結果を使って、非常に易しい結果を示すような感じになってしまう。

https://twitter.com/genkuroki/status/1627701924232564738

#統計 念の為のいつもの注意。

私は統計学についてはど素人です。

#統計 さらに補足

残差が非正規分布のi.i.d.であっても、nが十分に大きいなら、t分布はほぼ標準正規になるので、t分布を使って求められた線形回帰の(回帰直線(一般には回帰曲線)の)信頼区間の誤差も小さくなります。

予測区間の側については残差の非正規性に注意を払う必要がある。

#統計 補足。xの分布は正規分布。そのとき残差の値全体が正規分布になることは

* 独立な正規分布の和も正規分布(これはラフな言い方、注意)
* 正規分布の平均値μに関する正規分布での平均も正規分布

から出ます。

線形回帰可能な2つの群のデータが混じっている場合
↓

https://twitter.com/genkuroki/status/1627701826782117888

#統計 このスレッドを書いて再確認できたことは

　データの視覚化の重要性

および

　データの視覚化と解釈にはかなりの知識と理解力が必要なこと。

適切な視覚化のためにはモデルに関する理解が必要。単にグラフを描いて目で確認するだけのシンプルな作業ではない。もっと複雑なことをやっている。

#統計 説明用の例は、2次元(や3次元)のグラフを描けばすぐに分かるものを作るのですが、説明変数がたくさんある場合には、何をどのように視覚化すればモデルの失敗の程度を見ることができるかはずっと難しくなります。

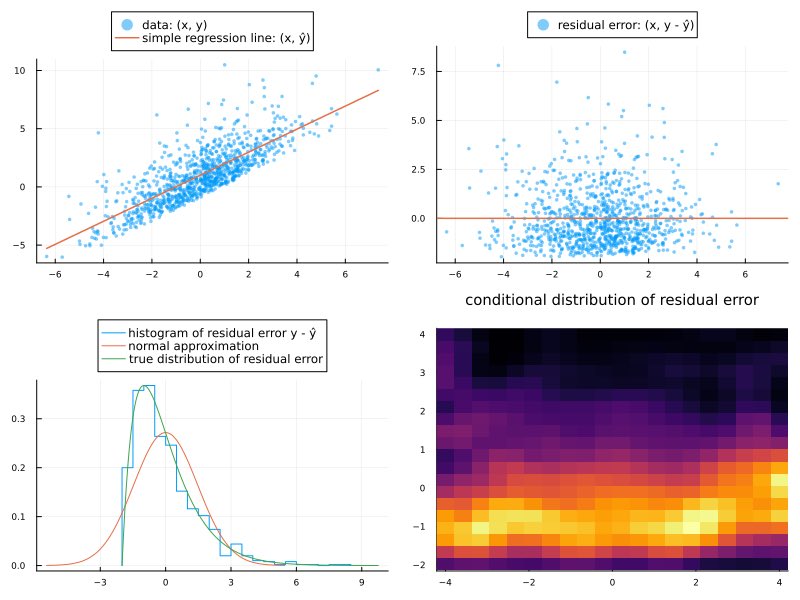
#統計 残差の分布がxを動かしたときに独立同分布になっていそうかどうかの、(x, 残差)の散布図での視認による確認は一般に困難です(xの分布が一様分布も場合は例外的)。

残差y-ŷの分布がxによらないのですが、添付画像の右上の散布図を見てもそうだと分からない。続く

https://twitter.com/genkuroki/status/1627701885011648512

#統計 そこで、kernel density 法で残差 y - ŷ のxに関する条件付き確率分布を推定して、ヒートマップでプロットしたものを追加してみました。概ね、条件付き確率分布がxにほぼよらないことが分かる。

nが小さいとこの辺の判断はさらに難しくなる。

#Julia言語
↓
github.com/genkuroki/publ…

#統計 実践的な統計学の適用はほぼ常に不良設定問題(与えられたデータだけでは信頼できる答えを出すことが不可能な問題)なので、データ以外の分野固有の特別な知識群で補強してやる必要が常にあると思います。

統計分析の結果を科学的に信頼できる客観的な判断だと安易に思ってしまうのはまずい。

#統計 あと、

❌最小二乗法をBLUE(最良線形不偏推定量)だという理由で最良の推定法だと考える

のも誤りです。

ほとんどに推定法は「不偏」という超絶強い条件を満たしません(し、線形でもない)。

BLUEは狭い世界での最強=「地元で最強」なだけ。

より適切なモデルによる推定法を常に考えるべき。

#統計 このスレッドで使っている #Julia言語 のコードを更新した。

github.com/genkuroki/publ…

#統計 大事なことなので、再度強調。

添付画像のように、(x, y-ŷ) = (x, 残差) の散布図を見ても、残差の分布がxに依存しているか否かはよくわかりません。分からない理由はこの場合にはxの分布が一様分布でないからです。

xごとの残差の分布を見て比較する必要がある。続く

#統計 添付画像は上の場合に、xで条件づけたときの残差の条件付き確率分布をカーネル密度法で推定した結果のヒートマップです。

これだと、横方向に似た分布が並んでいるように見える。

n=1000でもこれだけ粗い。nが小さいとよく分からなくなる。

#統計 iidの残差が正規分布でない場合の、データ達からは推定した回帰係数達の散布図とヒストグラム。

mvnormalapprox_true(～)は中心極限定理に基く、回帰係数の推定量の分布の漸近先の2変量正規分布。

fit(～)は実際の分布に最良適合する2変量正規分布。

ほぼ一致。

github.com/genkuroki/publ…

#統計 最小二乗法による回帰係数の推定は点推定に過ぎず、統計学のイロハの1つは

⭕️点推定値だけを報告してはいけない。

です。

⭕️点推定値の誤差の大きさの見積もり(例えば区間推定)の結果も報告するべき

です。1つ上のツイートの結果はそのために役に立ちます。続く

#統計 区間推定には多くの場合に正規分布近似を使います。

上の方で紹介した計算例は、iidの残差が正規分布にしたがっていなくても、回帰係数の推定量の分布は中心極限定理が効いてくれて、区間推定が近似的に可能になる場合。

BLUE云々よりもこういう話の方が実践的に重要だと思います。

#統計 本当に見たいのは条件付き確率分布の情報であるときには、単純に散布図を見ても条件付き確率分布の様子は分からないことに注意するべき。

残差の分布を確認するときには、まさにそういう状況になるので、この点はもっと強調されるべきだと思います。(だから繰り返す述べている。)

https://twitter.com/genkuroki/status/1627974156573880322

#統計 知りたい情報をグラフを描いて得るためには、たくさんのことを理解していてかつ、必要なグラフを描くためのコードを自分で書けるコンピュータに関するスキルも必要。

だから、相当に複雑で興味深い話題になると思います。

みんなで語ることによって社会的にノウハウを蓄積するべき事柄。

#統計 このスレッドを読んで、「あれ？残差がiidであることではなく、中心極限定理(の拡張)が成立していることの方が本質的じゃね？」と思った人は鋭いです。

回帰係数の推定量の分布が、中心極限定理(の拡張)によって多変量正規分布で近似されていれば、回帰係数の区間推定が可能になる。

#統計 ただし、一般的な中心極限定理もしくはその拡張による正規分布近似はn→∞で精密になることを言っているだけなので、実際に扱うnでの近似の良さの推測では「どのような場合にどれだけ中心極限定理による正規分布近似の精度が悪化するか」について理解しておく必要があります。これは結構難しい。