Share this page!

黒木玄 Gen Kuroki Profile picture
Twitter logo
Feb 22 • 13 tweets • 7 min read
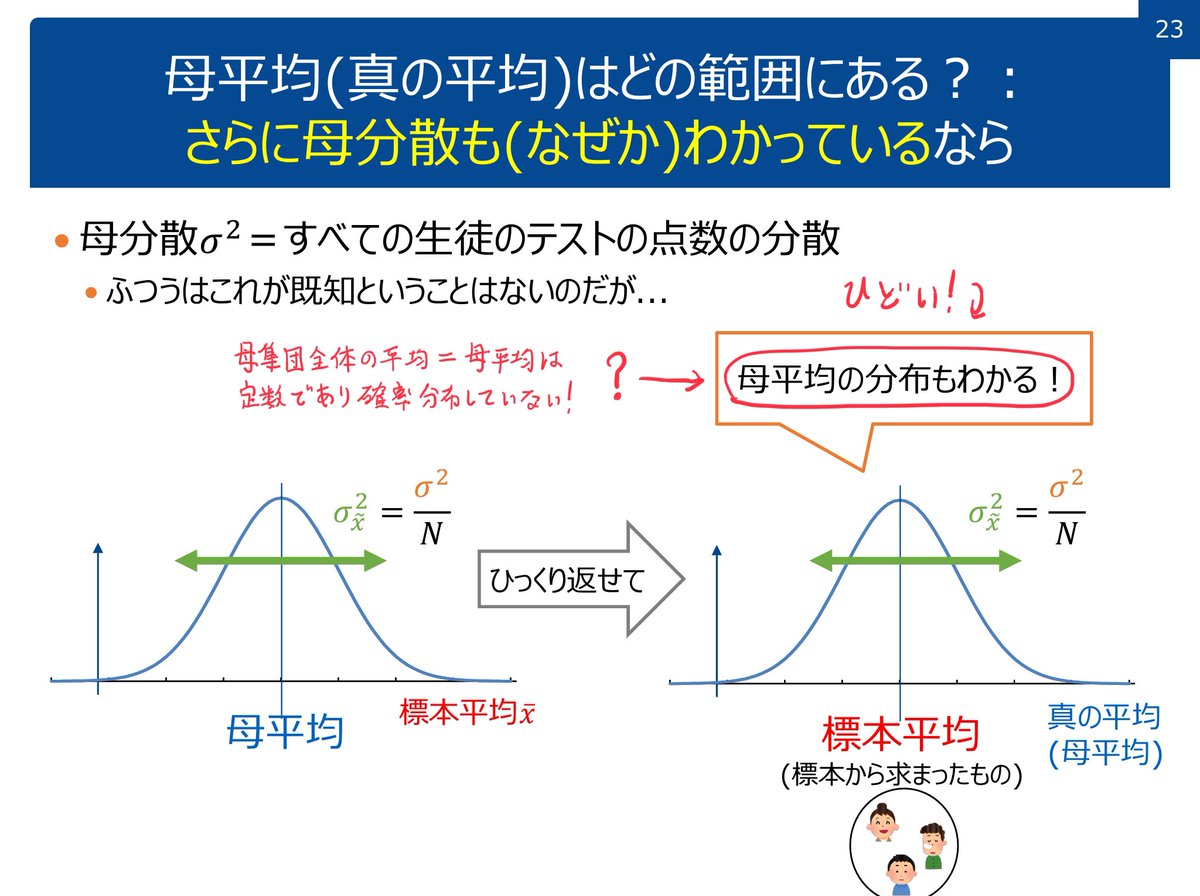
#統計 speakerdeck.com/taka88/pzhi-fa… のp.7からp.8への流れは、natureの記事の内容を誤解させるような、よろしくない解説の仕方だと思いました。

「差がない」という特別な帰無仮説の検定だけで勝負を決めようとすることへの批判をP値そのものへの批判とみなすことは、よく見る杜撰な考え方です。続く
#統計 実際、natureの記事 nature.com/articles/d4158… ではcompati{ble,bility}が重要キーワードになっており、P値が

データ、モデル、パラメータ値のcompatibility(相性の良さ、両立性)の指標の1つ

とみなされることを詳しく説明しています。

この部分に触れずにこの記事を引用しても無意味。続く
#統計 natureのその記事を読んでいるならば、P値のcompatibilityとしての解釈について知り、添付画像のように、ダメな考え方と正しい考え方を区別できるようになっているはずなのです。

否定するべき対象にP値そのものが含まれていないことに注目！

続く
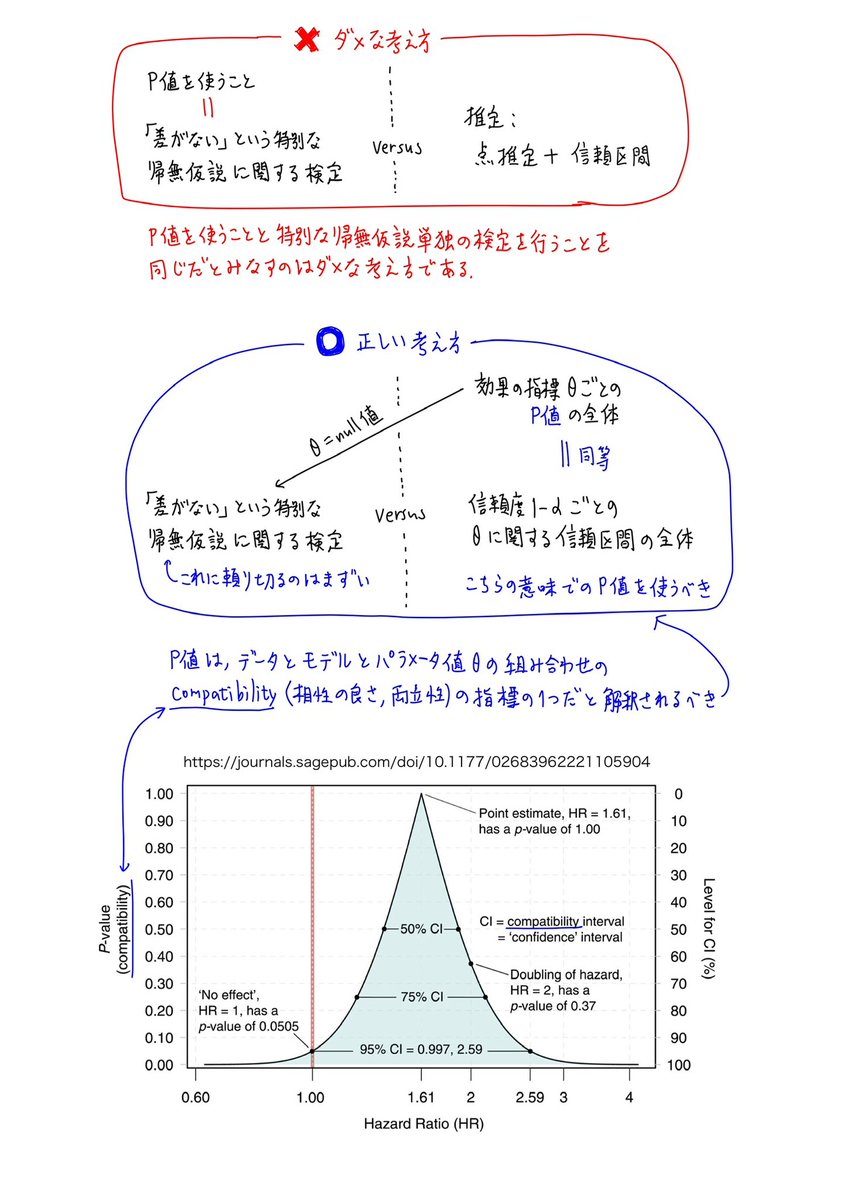
#統計 「効果がない」という特別な帰無仮説に関する単独のP値や検定だけで勝負を決めようとする態度を否定する常識的な考え方と、「P値や検定自体が否定されている」のような杜撰な考え方では大違いです。

後者は統計学教育の観点から有害なので、きちんと否定して行く必要があると思います。
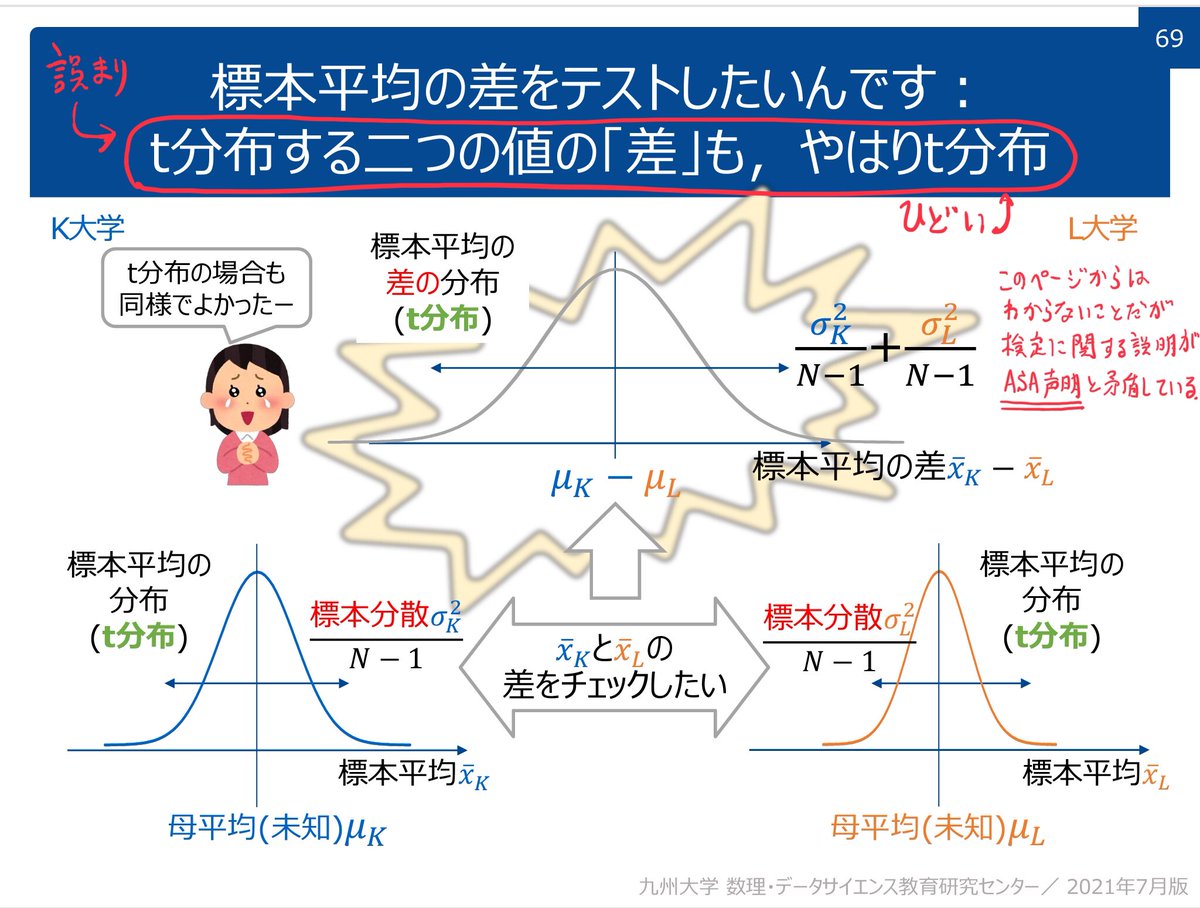
#統計 教育面での危惧は『統計的有意性とP値に関するASA声明』の翻訳者の佐藤俊哉さんも

jstage.jst.go.jp/article/jjb/38…

の最後の段落で表明しています(添付画像)。

検定と信頼区間の理論が表裏一体であることは多くの数理統計学の教科書で解説されている常識の1つだと思います(無知な人達に注意)。続く
#統計 P値や検定の全体を否定して、信頼区間の方を使うべきだ、と述べている人達は、基本的なことをよく理解せずに、統計学教育的に有害な意見を述べていることになります。

否定するべきなのは、特別な帰無仮説のP値や検定だけで勝負を決しようとする科学的に非常識な態度の方です。
#統計 「効果はない」という特殊な帰無仮説の検定を特別に重視する非常識な考え方を常識的に否定しつつ、P値や信頼区間の健全な使い方について知りたい人には次の短い論文がお勧めです。

これの著者は既出のnatureの記事の著者3人のうちの2人です。

journals.sagepub.com/doi/10.1177/02…
#統計 さらにそのnatureの記事のもう1人の著者とゲルマンさんの共著の次の論文もお勧めです。

stat.columbia.edu/~gelman/resear…

それらのどこでもP値の使用自体は否定されていません。

件のnarureの記事をろくに読まずに、統計学教育的に有害な言説を拡散する行為には明瞭に批判的であるべきだと思います。
#統計 おまけの余談

Greenlandさん達は信頼区間をcompatibility intervalと呼ぶことを提案しているのですが、McElreathさんはStatistical Rethinkingでベイズ信用区間もcompatibility intervalと呼んでおり、私もその考え方に賛成です。続く
#統計 余談続き

ベイズ統計での事後分布も、P値と同様に、

データの数値
モデル(事前分布を含む)
パラメータの値

の相性の良さ(compatibility, 両立性)の指標を与えているとみなせます。モデルに事後分布が含まれる点がP値の場合とは違っているが、考え方は同様で良い。
#統計 このスレッドで述べたことは、ツイッターで繰り返し述べていることなので、私のツイログ検索でより詳しい情報が得られます。

検索の例
↓
twilog.org/genkuroki/sear…
#統計 Statistical Rethinkingの2nd editionの1,2章はネットで公開されている。

xcelab.net/rmpubs/sr2/sta…

さらに講義の動画とスライドがGitHubで公開されている。

2022年
github.com/rmcelreath/sta…

2023年
github.com/rmcelreath/sta…

統計的因果推論入門になっている部分が多い。冗談が非常に多い！
#統計

統計的有意性とP値に関するASA声明の日本語版
biometrics.gr.jp/news/all/ASA.p…

翻訳者による講義動画
ocwcentral.com/subjects/01GB4…

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with 黒木玄 Gen Kuroki

黒木玄 Gen Kuroki Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @genkuroki

黒木玄 Gen Kuroki Profile picture
Feb 21
このツイートの存在にずっと気付いてなくて、昨晩読んでしまって笑い転げた。

やっぱり「知的レベルが低い」としか言いようがない。

今時の中学生はこの手のことを言うと馬鹿にされることをネットで見てよく知っているので、現代的には中学生にも馬鹿にされるレベルだと思います。
#統計

統計学ファンであれば、ゲルマンさんのブログで成田祐輔さんに関するNew York Timesでの記事が話題にされていることをすでに知っているはず。

ゲルマンさんのブログで悪い意味で取り上げられることは統計学方面では相当に怖いことだと思われます。

statmodeling.stat.columbia.edu/2023/02/13/yal…
#統計 リンク先に飛ぶのが面倒な人は添付画像の最初の部分だけに目を通すだけで雰囲気が分かると思います。

最後まで取っておいた最高のネタは専門の中に確率統計が入っていること(笑)

ゲルマンさんによれば【馬鹿げた操作変数法のパロディのようなもの】らしい。

statmodeling.stat.columbia.edu/2023/02/13/yal…
Read 14 tweets
黒木玄 Gen Kuroki Profile picture
Feb 20
#統計

正確な説明にこだわっているようなのであえてコメント。

線形回帰でこだわるべき条件は「残差が正規分布」よりも「残差が独立同分布」の方です。

残差が非正規分布のi.i.d.のときの線形回帰は、非正規母集団のt検定と同じようにうまく行ったり、行かなかったりします。詳しい解説に続く。
#統計 例で説明します。

まず、残差がi.i.d.ではないが、残差全体は正規分布に従う場合があることの説明。

添付画像がそのような場合の例になっています。

データの散布図(青点達)を見ると、この場合には単純な線形回帰の適用が不適切であることは明らか。続き#

nbviewer.org/github/genkuro… Image
#統計 この例は回帰直線を2本にする必要があります。

1本の回帰直線に関する残差の値全体の分布は正規分布になります。

添付画像①から残差の分布がxへの依存性が分かる。

添付画像②はxを無視すると残差全体は正規分布になることの確認。(理論的にそうなることも確認済み)

続く ImageImage
Read 33 tweets
黒木玄 Gen Kuroki Profile picture
Feb 19
最近ちょっと話題の中学校の数学の教科書にある「ねじれの位置」という用語についてですが、数学の理解には不要な用語であるとしっかり教えて行く必要があると私は思っています。

例えば「ねじれの位置にある線分の組み合わせはどれか？」のような試験問題を出した人には反省してもらう必要がある。
この手のことは他にもたくさんあり、近年、中学校数学の試験問題の質を大幅に下げていると思います。

「理解に不要な用語をわざわざ覚えたか」を問う有害な問題が理解度を問う問題であるかのように出題されているという問題。
子供に強制的に覚えさせたい用語については、強制する側がその強制が必要である理由を説明する責任があります。

それをせずに、その用語が不要な理由を私に質問するのは質問を急ぎ過ぎ。
Read 17 tweets
黒木玄 Gen Kuroki Profile picture
Jan 28
#統計 P値や信頼区間に関する大学での講義は(数え切れないくらい強調していることですが)、論文 journals.sagepub.com/doi/10.1177/02… の内容(過信や自信過剰を引き起こさない考え方)に従うように改訂されるべきだと思います。

過去の大学の講義のほとんどがその意味では失格。
#統計 帰無仮説は統計モデルのパラメータの値に関する仮説になっており、P値を得るための確率の(近似)計算は帰無仮説下の統計モデル内で行うことになるので、統計モデルについての説明がない仮説検定の説明は最初から相手にする価値がないということになります。
#統計 仮説検定における「統計モデル」は「P値の計算に使われる数学的仮定の全体」のようにざくっと定義しておくと便利です。

例えば、P値の計算に確率の近似計算を使うならば、その近似がうまく行くという条件が統計モデルの中に含まれていると考えると便利。
Read 10 tweets
黒木玄 Gen Kuroki Profile picture
Jan 28
#数楽

a(n+1)=3a(n)+2ⁿ は Ta(n)=a(n+1) を使えば

(*) (T-3)a(n)=2ⁿ

と書き直せる。(T-2)2ⁿ=0なので、

(*)⇒(T-2)(T-3)a(n)=0.

ゆえに(*)の解は

a(n)=A×3ⁿ+B×2ⁿ

と書ける。このとき(*)⇔B=-1.

以上の完全に機械的な解法は大幅に一般化可能。
#数楽 Ta(n+1)=a(n)と書く。

(Tⁿ+p₁Tⁿ⁻¹+…+pₙ)a(n) = 0

の形の斉次方程式の解の形が完全にわかっていることを使えば、f(n)がそのような形の斉次方程式の解であるときの

(Tⁿ+p₁Tⁿ⁻¹+…+pₙ)a(n) = f(n)

の形の非斉次の場合も機械的に解ける。技巧的な式の変形技術は無用になる。
#数楽 そういう技巧を不要にする機械的解法は、

　ある種の方程式を満たす数列全体の集合が具体的に完全にわかっていること

から、ただちに出て来る。

ある街の様子を完全に知っていれば、その街で苦労無しに快適に暮らせるのと似ている。
Read 8 tweets
黒木玄 Gen Kuroki Profile picture
Jan 27
#統計 mdsc.kyushu-u.ac.jp/lectures の mdsc.kyushu-u.ac.jp/wp/wp-content/… の内容が滅茶苦茶。添付画像を参照。

①信頼区間の説明で「母平均の分布もわかる！」と書いてある。酷い！

②「t分布する二つに値の「差」も、やはりt分布」と書いてある。酷い！

③Wilcoxonの順位和検定は中央値の差の検定法ではない。
#統計 P値や信頼区間に関するより現代的な知識は論文 journals.sagepub.com/doi/10.1177/02… で得られる。

統計的有意性とP値に関するASA声明 biometrics.gr.jp/news/all/ASA.p… は必読で、講義動画 ocwcentral.com/subjects/01GB4… には時代遅れな説明が書いてある教科書に批判的コメントがある。

これらの代替案に従えば無難。
#統計

mdsc.kyushu-u.ac.jp/lectures
↓
slideshare.net/ssuserf64eb4/s…

にも同様に酷い説明がある。

①真の平均が正規分布しているかのようなグラフの下に【真の平均は，95%の確率で，標本平均±1.96σ/√Nの範囲にある！】と書いてある！酷い。

②【t分布する二つの値の「差」も，やはりt分布】とある！酷い！
Read 5 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Don't want to be a Premium member but still want to support us?

Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal

Or Donate anonymously using crypto!

Ethereum

0xfe58350B80634f60Fa6Dc149a72b4DFbc17D341E copy

Bitcoin

3ATGMxNzCUFzxpMCHL5sWSt4DVtS8UqXpi copy

Thank you for your support!

Follow Us on Twitter!

Send Email!

:(