
Sabes que la multiplicación de #matrices es realmente importante en la computación cuántica.
Pues si, más concretamente en las llamadas puertas cuánticas.
Quédate, te lo cuento en este 🧵 donde además te lo enseño de manera práctica usando #Python y la librería @qiskit
Empezamos
Pues si, más concretamente en las llamadas puertas cuánticas.
Quédate, te lo cuento en este 🧵 donde además te lo enseño de manera práctica usando #Python y la librería @qiskit
Empezamos
Lo primero que debemos conocer es como se representa un qubit.
Un qubit (o bit cuántico) es el análogo cuántico de un bit clásico. Un qubit es un sistema cuántico de dos niveles donde los dos estados básicos del qubit generalmente se escriben como ||0⟩∣0⟩ y ||1⟩∣1⟩ .
Un qubit (o bit cuántico) es el análogo cuántico de un bit clásico. Un qubit es un sistema cuántico de dos niveles donde los dos estados básicos del qubit generalmente se escriben como ||0⟩∣0⟩ y ||1⟩∣1⟩ .

Un qubit puede estar en el estado ||0⟩∣0⟩,||1⟩∣1⟩ o (a diferencia de un bit clásico) en una combinación lineal de ambos estados.
¿Cómo en combinación de ambos?
Para ello debemos imaginarnos los estados en una esfera, la llamada esfera de Bloch.
Mira el estado ∣0⟩
¿Cómo en combinación de ambos?
Para ello debemos imaginarnos los estados en una esfera, la llamada esfera de Bloch.
Mira el estado ∣0⟩

Vamos representar este estado en #Python usando la librería @qiskit .
✅Cargamos las librerias
✅Creamos un circuito cuántico (1 qubit)
✅Representamos el estado [1,0]
Aquí tienes el código👇
✅Cargamos las librerias
✅Creamos un circuito cuántico (1 qubit)
✅Representamos el estado [1,0]
Aquí tienes el código👇

Bueno sigamos..expliquemos como podemos modificar su estado usando puertas cuánticas
Entran en acción las matrices
IMPORTANTE: a diferencia de las puertas de computación clásica, en un puerta cuántica el qubit origen se modifica mientras que en la clásica se mantiene intacto.
Entran en acción las matrices
IMPORTANTE: a diferencia de las puertas de computación clásica, en un puerta cuántica el qubit origen se modifica mientras que en la clásica se mantiene intacto.
Puerta NOT . Aplicada aún solo qubit
Se encarga de intercambiar las probabilidades de leer cero y uno, es decir cambiar el estado de 0 a 1 o viceversa.
Para ello usaremos la matriz unitaria con ceros en su diagonal principal
Mira como funciona 👇
Se encarga de intercambiar las probabilidades de leer cero y uno, es decir cambiar el estado de 0 a 1 o viceversa.
Para ello usaremos la matriz unitaria con ceros en su diagonal principal
Mira como funciona 👇
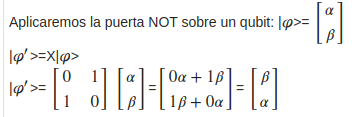
Ahora vamos aplicarlo en #Python.
✅ Reseteamos el estado del qubit
✅ Inicializamos el estado a [1,0]
✅ Aplicamos la puerta NOT
✅ Representamos
El código 👇
✅ Reseteamos el estado del qubit
✅ Inicializamos el estado a [1,0]
✅ Aplicamos la puerta NOT
✅ Representamos
El código 👇

La siguiente puerta se la conoce como Hadamard y es la que pone al qubit en estado de "superposición", es decir en un estado que nos es ni cero ni uno, "estado cuántico".
Mira como se representaría en la esfera de Bloch
Mira como se representaría en la esfera de Bloch

¿Que forma tiene una matriz para poder poner un qubit en ese estado?
Pues realmente el inverso de la Raíz de dos tiene gran parte de la culpa.
Mira como se representaría matemáticamente 👇
Pues realmente el inverso de la Raíz de dos tiene gran parte de la culpa.
Mira como se representaría matemáticamente 👇

Entendido matematicamente veamos como lo podemos aplicar con #Python.
Recordemos que aplicar una puerta Hadamard no deja de ser una rotación del estado de un qubit sobre uno de los ejes, de aquí que venga su llamada "superposición"
El código 👇
Recordemos que aplicar una puerta Hadamard no deja de ser una rotación del estado de un qubit sobre uno de los ejes, de aquí que venga su llamada "superposición"
El código 👇

Ahora veamos una puerta muy interesante, la llamada CNOT.
Es interesante porque se aplica sobre dos qubits a diferencia de lo que hemos estado haciendo anteriormente.
¿Como funciona?
El primer qubit es el controlador y el segundo qubit es el objetivo.
Te lo explico 👇🧵
Es interesante porque se aplica sobre dos qubits a diferencia de lo que hemos estado haciendo anteriormente.
¿Como funciona?
El primer qubit es el controlador y el segundo qubit es el objetivo.
Te lo explico 👇🧵
✅Cuando el primer qubit es |0> no se aplica nada al segundo qubit
✅Cuando el primer qubit es |1> se aplica una puerta X sobre el segundo qubit
Ohhh.. ¿y que matriz puede hacer esto?. Pues realmente una matriz de 4x4 (tenemos dos qubits)
Aquí a tienes 👇
✅Cuando el primer qubit es |1> se aplica una puerta X sobre el segundo qubit
Ohhh.. ¿y que matriz puede hacer esto?. Pues realmente una matriz de 4x4 (tenemos dos qubits)
Aquí a tienes 👇

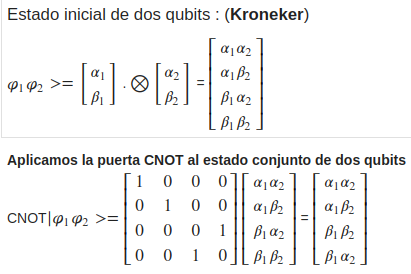
¿Y que operación matemática puedo hacer para que se produzcan esos cambios de estado?
Pues la verdad es más sencillo de lo que parece, pero debemos retomar el productor matricial de "Kroneker"
Mira este ejemplo 👇
Pues la verdad es más sencillo de lo que parece, pero debemos retomar el productor matricial de "Kroneker"
Mira este ejemplo 👇
Pero venga dejemos las matemáticas y veámoslo en #Python
✅ Creamos un circuito con 2 qubits
✅ Los inicalizamos en estados [0,1] y el otro en [1,0]
✅ Representamos
El código 👇
✅ Creamos un circuito con 2 qubits
✅ Los inicalizamos en estados [0,1] y el otro en [1,0]
✅ Representamos
El código 👇

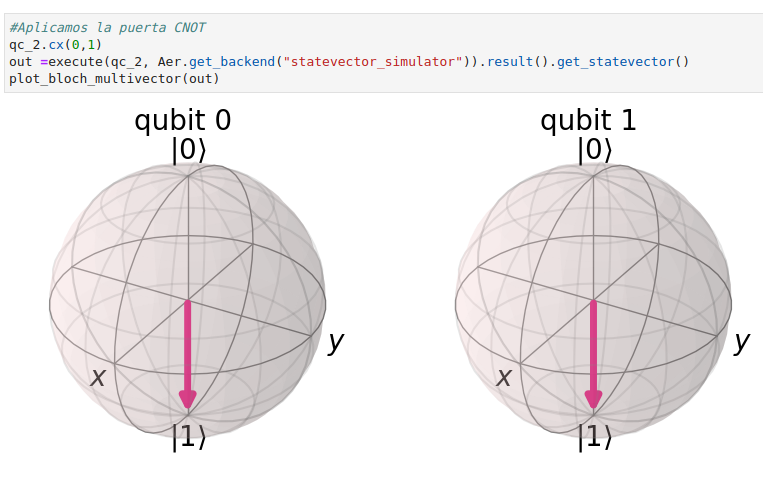
Ahora aplicamos en #Python una puerta CNOT la cual cambiará el estado del segundo qubit. 
Si os interesa la computación cuántica aquí os dejo un articulo más divulgativo sobre esta tecnología
magisnet.com/2022/07/la-com…
Tenéis todo el código explicado en este hilo en:
gist.github.com/jmcalvomartin/…
Fin 🧵
magisnet.com/2022/07/la-com…
Tenéis todo el código explicado en este hilo en:
gist.github.com/jmcalvomartin/…
Fin 🧵
• • •
Missing some Tweet in this thread? You can try to
force a refresh





